1. Introduction
1.1. Overview
Faim is a finite element solver optimized for solid mechanics simulations of bone, including strength and stiffness determinations, directly from three-dimensional medical image data such as micro-CT. Faim uses the mesh-free method, which is a highly memory efficient method of finite element analysis. This makes it possible to solve finite element models with very large numbers of degrees of freedom derived directly from high resolution scans.
The Faim Finite Element solver has an established record of being used in scientific studies. See the bibliography for selected studies.
1.2. How to read this manual
-
If you need to install Faim, refer to Installation in this chapter.
-
Experienced users may want to read What is new in version 9, and then go directly to the sections indicated there.
-
For new users, start by reading the section Work flow for finite element analysis. This will give you an overview of finite element analysis and the Numerics88 software tools.
-
Next, we recommend that you jump first to An introductory tutorial: compressing a solid cube. It will take you through the typical steps of generating a model, verifying it, solving it, and analyzing the results. This is a good introduction to how everything fits together, and will help to put things into context.
-
The intervening chapters (preceeding the Tutorials chapter) should be used as reference material. You probably don’t want to read them from beginning to end in one sitting with the intention of retaining everything; however, you should at least skim through them to be aware of the options, limitations and potential pitfalls.
-
If you are a user who is familiar with
n88modelgeneratorand who is interested in creating your own custom models, start with the tutorial, Compressing a cube revisited using vtkbone. And then move on to the more advanced tutorials dealing withvtkbone.
1.3. What is new in version 9
Version 9 introduces the following new features:
-
n88pistoia allows the user to set different critical strain and critical volume values when estimating failure load.
-
Code segments have been updated for newer versions of VTK (8.2.0) and Python (3.7). For example, the print statements used in Python 3 are different than Python 2.
1.4. Installation
In version 9, the installation of Faim is more modular than in previous versions.
1.4.1. Install the solvers and n88modelgenerator
The solvers and n88modelgenerator are the non-open sourced components of Faim and require a license file to run. They are bundled together into installers that can be downloaded from https://numerics88.com/downloads/ .
The Linux installer will be named something like faim-9.0-linux.sh. It can be installed
with the following command for a single user:
bash faim-9.0-linux.sh
For a system-wide installation, add sudo:
sudo bash faim-9.0-linux.sh
If you want to specify a particular install location, use the --prefix flag, for example
bash faim-9.0-linux.sh --prefix=$HOME/Numerics88
The Windows installer will be named something like faim-9.0-windows.exe. Simply run
it to install.
The Mac installer is a disk image with a name like faim-9.0-windows.dmg. Double-click
to mount it, and then drag the Faim icon to the Applications folder, or to any other
convenient location.
For all operating systems, it is possible to install Faim system-wide using an administrator account or for a single user, for which administrator rights are not needed. It is also possible to install it multiple times on a single machine, so that each user has their own installation. The installation directory can also be freely renamed and moved around.
1.4.2. How to run the solvers
To run the solvers and n88modelgenerator, you may use any of the following methods:
-
Run them with the complete path. For example
/path/to/faim/installation/n88modelgenerator
or, on Windows
"c:\Program Files\Faim 9.0\n88modelgenerator"
-
Permanently add the directory where they are installed to your PATH variable. The exact method depends on your operating system.
-
Run the script
setenvin a Terminal (or Command Prompt on Windows) to set the PATH just for that Terminal. On Linux and macOS, this is done as followssource /path/to/faim/installation/setenv
On Windows, if you are using a Command Prompt, then you can run
"c:\Program Files\Faim 9.0\setenv.bat"
while for Windows PowerShell, the equivalent is
. "c:\Program Files\Faim 9.0\setenv.ps1"
|
|
In version 9, the solvers and n88modelgenerator are statically linked.
Setting LD_LIBRARY_PATH (Linux) or DYLD_LIBRARY_PATH (macOS) is no longer required.
|
1.4.3. Install a license file
To receive a license file, you must run one of the Faim programs with the --license_check option, and send the resulting UUID to skboyd@ucalgary.ca . For example,
> n88modelgenerator --license_check n88modelgenerator Version 9.0 Copyright (c) 2010-2020, Numerics88 Solutions Ltd. Host UUID is DFD0727B-89AA-4808-B03F-E73E80ABFE64
When you receive a license file, which is a short text file, you can copy it to one of several possible locations where the software can find it. These locations are:
-
a subdirectory
licensesof the installation directory, or -
the location specified by the environment variable
NUMERICS88_LICENSE_DIR, if set, -
for an individual user, a directory
Numerics88/licenses(Numerics88\licenseson Windows) in their home directory, or -
on Linux,
/etc/numerics88/licenses, or -
on macOS,
/Library/Application Support/Numerics88/licenses, or$HOME/Library/Application Support/Numerics88/licenses, or -
on macOS,
/Users/Shared/Numerics88/licenses.
You may have multiple license files installed at once.
1.4.4. Install n88tools and vtkbone
The solvers and n88modelgenerator are most conveniently used together with
a collection a command-line utilities called n88tools. n88tools
is implemented in Python, and depends on the library vtkbone. Additionally,
vtkbone can be used to create custom model generation and processing scripts
in Python, as will be discussed in a subsequent chapter.
n88tools and vtkbone are open-source. If you wish, you can download the
source code from https://github.com/Numerics88/ and compile them yourself,
using whatever installation of Python is most convenient for you.
Most users however, will not want to go through the hassle of compiling them.
The quickest way to install them is via Anaconda Python, which is supported
on Linux, Windows, and macOS. An advantage of using Anaconda Python is
that the very large repository of mathematical and scientific Python
packages available in Anaconda Python can be used together with Faim.
To install n88tools and vtkbone in Anaconda Python, follow these steps:
-
Install Anaconda Python from https://www.anaconda.com/distribution/ . It is also possible to install Miniconda (http://conda.pydata.org/miniconda.html). Miniconda is identical to Anaconda, except that instead of starting with a very large set of installed python packages, it starts with a minimal set. You can of course add or subtract packages to suit your needs. Anaconda Python can be installed either system-wide, or just for an individual user. Faim works with either arrangement.
-
Create an Anaconda environment in which to run Faim. To learn about Anaconda environments, we recommend that you take the conda test drive at http://conda.pydata.org/docs/test-drive.html . Creating an Anaconda environment for Faim is optional; you could alternatively install
n88toolsandvtkbonedirectly in the root environment of Anaconda. However, using a dedicated enivornment greatly helps with avoiding possible conflicts, where for examplevtkbonemay want a specific version of a dependency, while some other Python package that you want to use requires a different version of the same dependency. In addition, you can create separate environments for different versions ofn88toolsandvtkbone, and easily switch between them. To create an Anaconda environment namedfaim-9.0and installn88toolsversion 9.0 andvtkboneall in one step, run the following command:conda create --name faim-9.0 --channel numerics88 --channel conda-forge python=3.7 n88tools numpy scipy
To use n88tools, you simply activate the Anaconda environment. On Linux and macOS,
this is done with
conda activate faim-9.0
On Windows, the command is
activate faim-9.0
You will have to activate the environment in each Terminal (or Command Prompt) in which you want to use Faim.
1.4.5. Install the Numerics88 plugins for ParaView
ParaView can be used for interactive rendering of Faim finite elements models.
For this purpose, Numerics88 provides plugins for ParaView. These allow
ParaView to open n88model files (as well as Scanco AIM files). The plugins
can be downloaded from http://numerics88.com/downloads/ . You can unzip
the plugins into any convenient directory, and you can move and rename
the plugin directory as you like.
|
|
The ParaView plugins are specific to a particular version of ParaView and can not be loaded into a different version of ParaView. |
To load the plugins, open ParaView, and select the menu item . The Plugin Manager will appear, as shown in Figure 1.
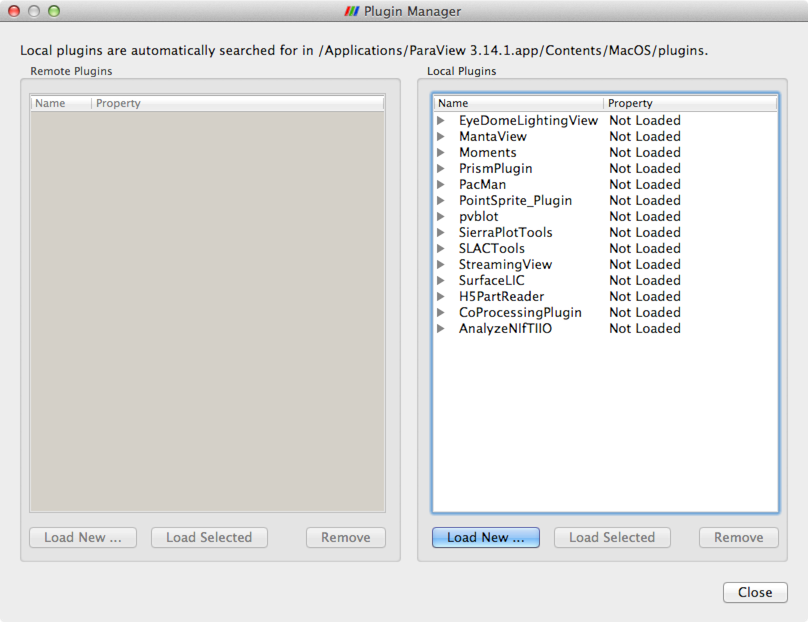
Click Load New… and navigate to the location of the plugins. Select one of the plugins, and then click OK. You will need to repeat this for each of the plugins, in particular for
-
libAIMReader, -
libImageGaussianSmooth, and -
libN88ModelReader.
They are now loaded, and you should be able to read to corresponding file
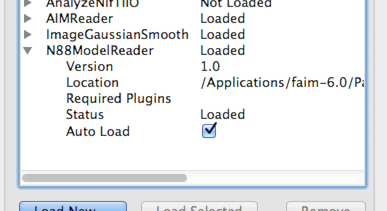
formats. You may want to select Auto Load for each plugin so that you don’t need to load them every time you open Paraview. To do this, click the drop-down arrow beside the plugin in the
Plugin Manager, and make sure that Auto Load is selected. This is
shown in Figure 2.
1.4.6. Additional downloads
A PDF version of this manual can be downloaded from http://numerics88.com/documentation/ .
Example data files, together with scripts for the tutorials in this manual, can be downloaded from http://numerics88.com/downloads/ .
1.5. Work flow for finite element analysis
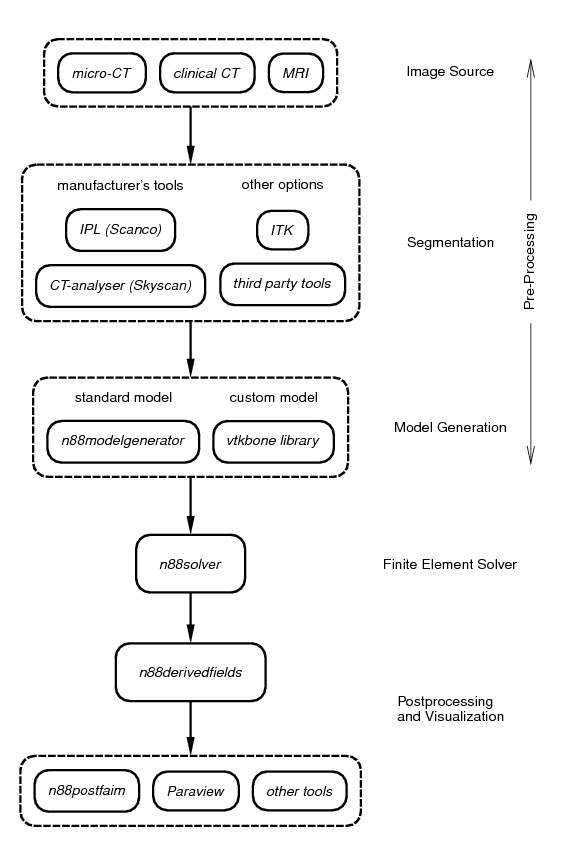
There are several steps involved in applying finite element analysis to 3D medical image data. These steps are diagrammed in Figure 3. Generally they can be categorized as pre-processing, solving, and post-processing. Faim integrates these steps to simplify the work flow as much as possible, while retaining flexibility and customizability in preparing, solving and analyzing finite element problems derived from micro-CT data.
1.5.1. Segmentation
The first step is to segment your 3D medical image data. Although in principle any type of 3D image data can be analyzed, we focus on the use of micro-CT images of bone here. During segmentation, bone and other relevant structures in the CT image are labelled and identified. Segmentation is a very broad and complex field. Because of this, Numerics88 software does not attempt to provide all solutions. Instead, we recommend that you use the segmentation tool provided by the manufacturer of your medical image equipment. This has the advantage that it will be well-integrated into the scanning workflow. In the case of Scanco systems, the tool is Image Processing Language (IPL); for Skyscan systems, CT-analyzer provides segmentation functionality.
In cases where your segmentation problem is unusually tricky and beyond the abilities of the manufacturer’s tools, there are many third party solutions available.
Whichever tool you use to perform the segmentation, the result should be a 3D image file with integer values. These integer values are referred to as "Material IDs", because they will subsequently be associated with abstract mathematical material models. Material ID zero indicates background material (often air, but sometimes also other material, such as marrow in bone) that can be assumed to have negligible stiffness. Voxels with material ID zero will not be converted to elements in the FE model. Other values can be associated freely with particular materials or material properties as required.
1.5.2. Model generation
Model generation is the process of converting a segmented image to a geometrical representation suitable for finite element analysis, complete with suitable constraints such as displacement boundary conditions and applied loads.
A number of steps are required for complete model generation.
- Meshing
-
Meshing is the process of creating a geometric representation of the model as a collection of finite elements. For micro-CT data, we typically convert each voxel in the input image to a hexahedral (box-shaped) element in the FE model. Each of the corners of the voxel becomes a node in the FE model. Voxels labelled as background (e.g. 0) are ignored.
|
|
There may be scenarios in which it is desirable to have FE models that have elements smaller or larger than the voxels of the available image. Larger elements lead to smaller FE models (i.e. fewer degrees of freedom) which may solve faster, at the expense of accuracy. Smaller elements allow the forces and displacements to vary more smoothly (that is, with higher resolution) in the FE model, at the cost of increased solution time and memory requirements. To alter the FE model from the original 3D image, one typically resamples the original image to the desired resolution employing some sort of interpolation. |
- Material Assignment
-
Material assignment is the process of mapping material IDs to mathematical models for material properties. For example, an isotropic material is specified by its Young’s modulus (E) and Poisson’s ratio (ν).
- Assigning Boundary Conditions and Applied Loads
-
Boundary conditions and applied loads implement a specific mechanical test. The tool used will typically translate a desired physical action, such as a force or a displacement applied to a specific surface, into a set of constraints on a set of nodes or elements.
Faim provides two tools for model generation:
- n88modelgenerator
-
n88modelgeneratoris a program that can generate a number of standard tests (e.g. axial compression, confined compression, etc…).n88modelgeneratorhas a number of options that allow for flexibility in tweaking these standard models.n88modelgeneratoris the easiest method of generating models. - vtkbone
-
vtkboneis a collection of custom VTK objects that you can use for creating models, and is a more advanced alternative to usingn88modelgenerator. In order to use them, you need to write a program or script (typically in Python). Some learning curve is therefore involved, as well as the time to write, debug and test your programs. The advantage is nearly infinite customizability. VTK objects, includingvtkboneobjects, are designed to be easily chained together into execution pipelines. In this documention, we will give many examples of usingvtkbonein Python scripts.
1.5.3. Finite element solver
The finite element solver takes the input model and calculates a solution of the displacements and forces on all the nodes, subject to the specified constraints.
As finite element models derived from micro-CT can be very large, the memory efficiency and speed of the solver are important. Faim uses a mesh-free preconditioned conjugate gradient iterative solver. This type of solver is highly memory efficient.
|
|
Faim is currently limited to small-strain solutions of models with linear and elastoplastic material definitions. This is adequate for most bone biomechanics modelling purposes, as bone undergoes very little strain before failure. However, if you need to accurately model large deformations, the Faim solver is not an appropriate tool. |
1.5.4. Post-processing and visualization
Post-processing and visualization can take many different forms, depending on the goals of your analysis. For example, you may want to identify locations of stress variations, in which case, a visualization tool is likely the best approach. Or, you may want to obtain a basic output such as an overall stiffness. A number of common post-processing operations are performed by Faim.
Visualization is important even in cases where ultimately you want one or more quantitative values. Visualization provides a conceptual overview of the solution, and may allow one to quickly identify incorrect or invalid results due to some deficiency in the input model. Many visualization software packages exist. If you don’t have an existing favourite package, we recommend the use of ParaView, which is an open-source solution from Kitware. The Faim distribution includes plug-ins for ParaView which allow ParaView to directly open Faim file types.
1.6. Units in Faim
Faim is intrinsically unitless; you may use any system of units that are self-consistent.
Nearly all micro-CT systems use length units of millimetres (mm). With forces in Newtons (N), the consistent units for pressure are then megapascals (MPa), as 1N/(1mm)2 = 1MPa. Young’s modulus is an example of a quantity that has units of pressure. In the examples, we will consistently use these units (mm, N, MPa).
2. Preparing Finite Element Models With n88modelgenerator
2.1. Running n88modelgenerator
n88modelgenerator is a tool to create a number of different standard mechanical test simulations directly from segmented 3D images. This tool is designed to be simple to use and in many cases, requires no more than specifying a test type and an input file, like this
n88modelgenerator --test=axial mydata.aim
This will generate a file mydata.n88model that is suitable as input to the
Faim solver.
|
|
For an introduction to n88modelgenerator, we recommend that you start first with An introductory tutorial: compressing a solid cube. Getting your hands dirty as it were with the program is often the best way to learn. Once you have some familiarity with the program, the following documentation will make much more sense. |
The models produced by n88modelgenerator can be modified and tuned by specifying a number of optional parameters. For example, here n88modelgenerator is run to create an axial test with a specified compressive strain and Young’s modulus:
n88modelgenerator --test=axial --normal_strain=-0.01 --youngs_modulus=6829 test25a.aim
Parameters can be specified either on the command line, or in a configuration
file. Command line arguments must be preceded with a double dash (--). The argument
value can be separated from the argument name with either an equals sign (=)
or a space. A complete list of all possible arguments is given in
the Command Reference chapter.
You can also run n88modelgenerator with the --help option to get a complete
list of possible parameters.
All parameters except the input file name are
optional; a default value will be used for unspecified parameters.
To use a configuration file, run n88modelgenerator as follows.
n88modelgenerator --config=mytest.conf test25a.aim
Here we are specifying the name of the input file on the command line.
This is convenient if we want to use the same configuration file for
multiple input files. It is also possible to specify the name of the
input file in the configuration file, using the option
input_file. The output file name is left
unspecified, so a default value will be used (test25a_axial.n88model in
this case), but it can also be specified either on the command line or
in the configuration file if desired.
The configuration file format is one line per option: the
parameter name (without leading dashes), followed by the equals character (=),
followed by the parameter value.
Lines beginning with # are ignored.
The following configuration file is exactly equivalent to the example
above using command line parameters.
# This is the example configuration file "mytest.conf" test = axial normal_strain = -0.01 youngs_modulus = 6829
|
|
If a parameter is specified on both the command line and in a configuration file, the command line value takes precedence. |
n88modelgenerator can accept several different input file formats. Refer to the Command Reference chapter for details.
|
|
If you have an input image in a different format, there are many
possible solutions. One is to convert the file format, possibly with
ParaView, which can read a large number of formats. VTK can also be
used to convert many image files. For example, the following python script
will convert a MetaImage format file to a VTK import vtk
reader = vtk.vtkMetaImageReader()
reader.SetFileName ("test.mhd")
writer = vtk.vtkXMLImageDataWriter()
writer.SetFileName ("test.vti")
writer.SetInputConnection (reader.GetOutputPort())
writer.Update()
For more information on scripting, refer to Preparing Finite Element Models With vtkbone. |
2.2. Test orientation
To allow for flexibility in defining the orientation of applied tests, two coordinate frames are defined:
- Data Frame
-
The Data Frame is the coordinate frame of the data. The input and output data use the same coordinate system.
- Test Frame
-
The Test Frame is the coordinate frame in which the test boundary conditions are applied. Tests are defined with a constant orientation in the Test Frame.
The relationship between the Test Frame and the Data Frame is set by the value
of the parameter test_axis according to the following
figure. In the figure, the red-colored axis is the test axis. What this
implies exactly depends on the kind of test that is being applied. For
example, for a compression test, the direction of compression is along the test
axis. The test axis is always the z axis in the Test Frame, and always equal
to value of the parameter test_axis in the Data Frame. The
default value for test_axis is z ; for this case the Test Frame and the
Data Frame coincide, as shown.
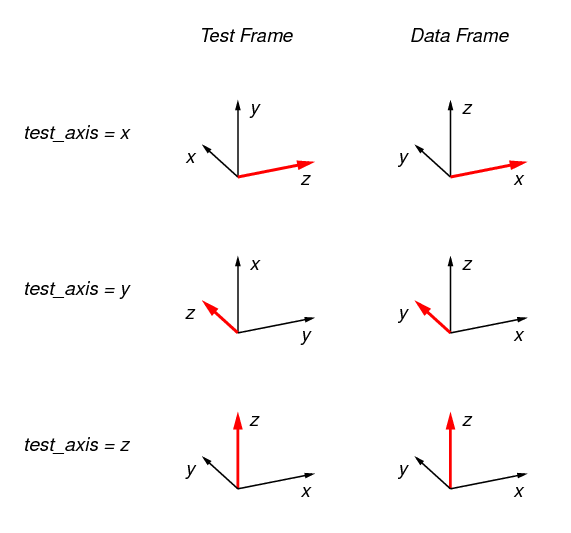
In the test descriptions, references to “Top” refer to the maximum z surface in the Test Frame; References to “Bottom” refer to the minimum z surface in the Test Frame. Likewise “Sides” refers to the surfaces normal to the x and y axes in the Test Frame.
The Test Frame is used only for the specification of tests (i.e. a specific configuration of boundary
conditions and applied loads) within n88modelgenerator and vtkbone. When the
model is written to disk as an n88model file, it is encoded
with reference to the original Data Frame. As a consequence
post-processing and visualization are in the original Data Frame.
|
|
In terms of rotations, for a setting of test axis = x, the transformation from the Test Frame to the Data Frame is a rotation of -90º about the x axis, followed by a -90º rotation about the z' axis. For a setting of test axis = y, the transformation from the Test Frame to the Data Frame is a rotation of 90º about the y axis, followed by a 90º rotation about the z' axis. These transformation sequences are of course not unique. For most applications, it is not necessary to know these transformations; it should be sufficient to refer to Figure 4. |
2.3. Standard tests
|
|
Axis directions in the following test descriptions are in the Test Frame. All the standard tests can be applied along any axis of the data by specifying test_axis, as described in the previous section. |
2.3.1. Uniaxial test
A uniaxial test is a compression (or tension) test with a fixed displacement or force applied along the z axis. Two boundary conditions are applied:
-
Nodes on the bottom surface are fixed in the z direction, but free in the x and y directions.
-
Nodes on the top surface are subject to a fixed displacement in the z direction. No constraints are applied to the x and y directions.
A uniaxial test is shown in Figure 5, along with other types of compression tests. The coordinate system shown in the figure is the Test Frame. A uniaxial test is distinguished from an axial test (described below) by the fact that nodes on the top and bottom surfaces are unconstrained laterally. This corresponds to zero contact friction.
The amount of displacement applied to the top surface can be specified by either the normal_strain or displacement parameters.
|
|
Uniaxial models are under-constrained since, as defined, arbitrary lateral motion, and arbitrary rotation about the z axis of the entire model are permitted. This results in a singular system of equations. A "pin" may be added to prevent these motions. See pin parameter. However, Faim will find a (non-unique) solution even without a pin, and in fact typically does so faster in the absence of a pin. A pin should always be added if you want to use an algebraic solver, or if you intend to compare the absolute positions of multiple solved models. Alternatively, you can register the solved models before comparing absolute positions. |
2.3.2. Axial test
An axial test is similar to a uniaxial test, with the additional constraint that nodes on the top and bottom surfaces are also laterally fixed (i.e. no movement of these nodes is permitted in the x-y directions). This corresponds to 100% contact friction.
An axial test is shown in Figure 5.
2.3.3. Confined test
A confined test is similar to an axial test, with the addition that nodes on the side surfaces of the image volume are constrained laterally (i.e. no movement of these nodes is permitted in the x-y directions).
A confined test is shown in Figure 5.
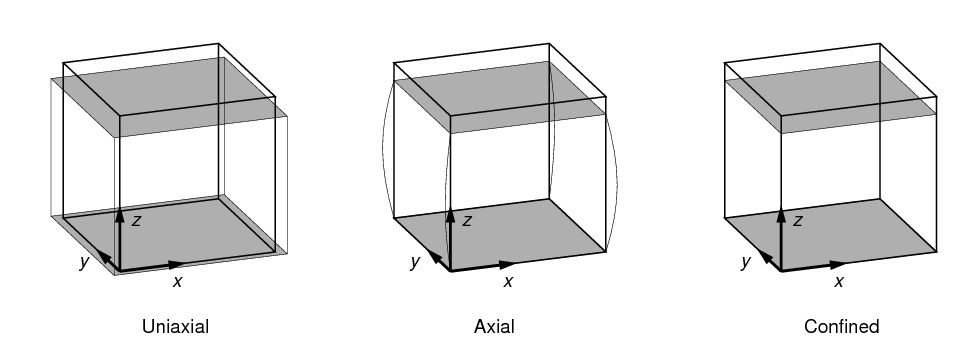
2.3.4. Symmetric shear test (symshear)
In a symmetric shear test, the side surfaces are angularly displaced to correspond to a given shear strain. This is shown in Figure 6. The only parameter of relevance to a symmetric shear test is shear_strain.
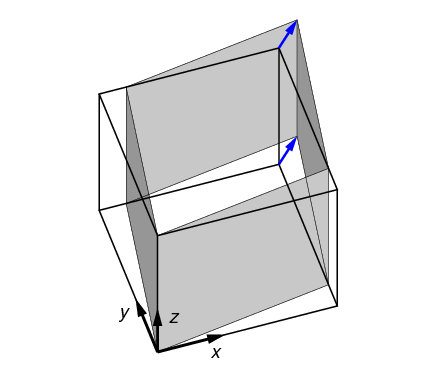
2.3.5. Directional shear test (dshear)
In a directional shear test, the top surface is displaced laterally, as shown in
Figure 7. The direction and degree of displacement are
set by the parameter shear_vector,
which gives the x,y shear displacement in the Test Frame.
Typically shear_vector is unitless, and the actual displacement
is the shear vector scaled by the vertical height of the model (i.e.
the image extent in the z direction in the Test Frame).
If however scale_shear_to_height
is set to off, then shear_vector is taken to have absolute units of
length.
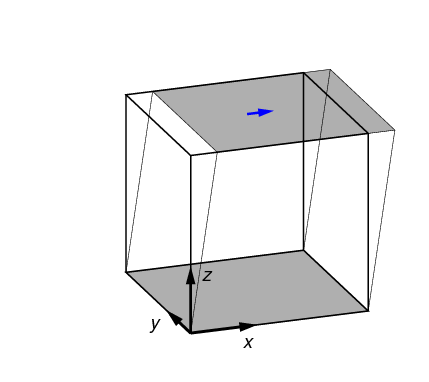
2.3.6. Bending test
In a bending test, the top and bottom surfaces are rotated in opposite
directions, as shown in Figure 8. The rotation axes are defined by
a neutral axis, given by a point in the x,y plane (shown as C) and an
angle in the x,y plane. (The coordinate system shown in
the figure is the Test Frame.) The neutral axis, projected onto the top and
bottom surfaces, is indicated in
blue in Figure 8.
The point and angle defining the neutral axis can be set in
n88modelgenerator with the parameters
central_axis and
neutral_axis_angle respectively.
The central axis (point C) can be specified as a numerical x,y pair, or as the
center of mass or the center of the data bounds; center of mass is the default setting.
The default angle of the neutral axis is 90º, parallel to the y-axis.
The amount of rotation can be specified with the parameter bending_angle. The top and the bottom
surfaces are each rotated by half of this value. Positive rotation is defined as in Figure 8.
In a bending test, the top and bottom surfaces are laterally constrained; no x,y motion of the nodes on these surfaces is permitted.
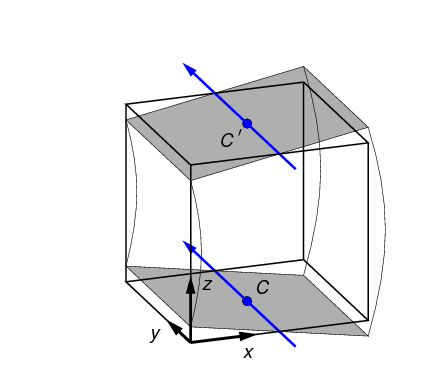
2.3.7. Torsion test
In a torsion test, the top surface is rotated about the center axis, as shown in Figure 9. The angle of rotation is given by twist_angle. In the figure positive rotation is shown. The central axis lies parallel to the z axis in the test frame; its position can be specified with the parameter central_axis. The default position of the central axis is passing through the center of mass.
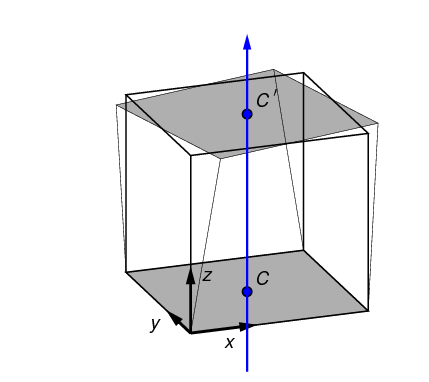
2.4. Uneven surfaces
The grey planes in Figure 5 represent the top and bottom boundary surfaces of the image volume. The actual surface to which boundary conditions are applied is by default that part of your object which passes through these boundaries. If your object does not intersect with the top and bottom boundaries of the image volume, then no boundary conditions can be applied using this method.
An alternative is to make use of the parameters top_surface and bottom_surface. The “uneven surface” near a boundary is defined as the surface visible from that boundary (viewed from an infinite distance). Visibility is evaluated using ray tracing. Thus for a porous material such as bone the “uneven surface” consists of nodes on the top visible surface, not including nodes on surfaces down inside the pores.
The visible setting can be used for any type of test except symshear. For example, if used with a
bending test, the boundary conditions are no longer exactly tilted planes as shown
in figure Figure 8; the displacement of each node on the visible surfaces is still
calculated as described from its x,y coordinates, but the displaced nodes
no longer lie all on a plane (because the initial positions are not on a plane.)
Because the visibility test may find some surfaces far from the boundary in question, it should usually be used together with the parameters bottom_surface_maximum_depth and/or top_surface_maximum_depth. These provide a limit, as a distance from the boundary, for the search for the uneven surface.
2.5. Material specification
Material specification consists of two parts:
- Material Definition creation
-
One or more material definitions are created. A material definition is a mathematical description of material mechanical properties. It has a definite type (e.g. linear isotropic or linear orthotropic) and specific numerical values relevant to that type (e.g. a linear isotropic material definition will have particular values of Young’s modulus and Poisson’s ratio).
- Material Table generation
-
The material table maps material IDs, as assigned during segmentation, to material definitions. It is possible to combine different types of materials (e.g. isotropic and orthotropic) in the same material table. A single material definition can be assigned to multiple material IDs.
In Numerics88, material definitions are indexed by name. This is not usually
evident in
n88modelgenerator, as for basic usage, the names are generated automatically,
and are not needed by the user. However for advanced material specification,
this becomes important, as we will see below when material definition
files are discussed.
2.5.1. Elastic material properties
Linear elastic materials obey Hooke’s Law,
where εxx,εyy,εzz are the engineering normal strains along the axis directions, γyz,γzx,γxy are the engineering shear strains, and σij are the corresponding stresses. S is the compliance matrix. The inverse of S gives σ in terms of ε, and is the stress-strain matrix C, also sometimes called the stiffness matrix.
An isotropic material has the same mechanical properties in every direction. Elastic isotropic materials are characterized by only two independent parameters: Young’s modulus (E) and Poisson’s ratio (ν). The compliance matrix is
For n88modelgenerator the isotropic elastic parameters are set with youngs_modulus and poissons_ratio. The default values are 6829 MPa and 0.3, as reported by MacNeil and Boyd (2008).
An isotropic material definition is the default, and will be assumed if no other material type is specified.
Orthotropic elastic materials have two or three mutually orthogonal twofold axes of symmetry. The compliance matrix is
where
| Ei |
is the Young’s modulus along axis i , |
| νij |
is the Poisson’s ratio that corresponds to a contraction in direction j when an extension is applied in direction i , |
| Gij |
is the shear modulus in direction j on the plane whose normal is in direction i . It is also called the modulus of rigidity. |
Note that the νij are not all independent. The compliance matrix must be symmetric, hence
Therefore only 9 independent parameters are required to fully specify an orthotropic material.
For n88modelgenerator the orthotropic elastic parameters are set with orthotropic_parameters. Whenever this parameter is specified, an orthotropic material definition will be used.
|
|
An orthotropic material defined with a compliance matrix as given above necessarily has its axes of symmetry aligned with the coordinate axes. In contrast, an orthotropic material which is rotated relative to the coordinate axes has a more general form of compliance matrix. In Numerics88 software, such a non-aligned orthotropic material must be specified as an anisotropic material. A rotation matrix relates elements of the anisotropic compliance matrix to the orthotropic compliance matrix. If you want the mathematical details, please contact us! |
The most general form of an elastic material is anisotropic, for which
we allow the stress-strain matrix, or the compliance matrix, to have arbitrary values.
The stress-strain matrix is symmetric, therefore an anisotropic material requires
21 parameters to define.
To define an anisotropic material with n88modelgenerator, it
is necessary to use a
material definitions file. See below.
2.5.2. Plasticity
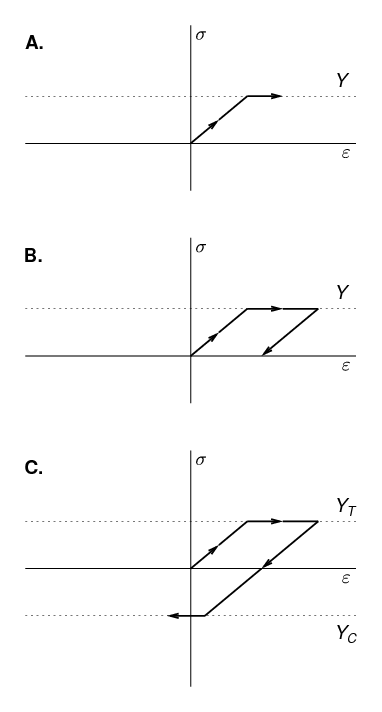
Elastoplastic material behaviour is an idealisation of a particular kind of nonlinear stress-strain relationship in which we divide the stress-strain relationship into two clearly distinguished regions: (1) an elastic region, which is identical to the linear elastic material behaviour described above, and, (2) a purely plastic region. For a material subject to a uniaxial deformation, this is sketched in Figure 10. In Figure 10A, we see the initial elastic region, which in this sketch is tensile, with slope equal to the Young’s modulus. This region continues until the stress reaches the yield strength, Y. For further increases in strain beyond this point, the stress ceases to increase, and remains constant at the yield strength. The incremental strain in this region is referred to as the plastic strain. Although we must perform work to produce a plastic strain, the plastic strain is irreversible, as can be seen in Figure 10B. In B, after applying a large plastic strain, the strain is gradually reduced. The plastic strain component is unchanged during the relaxation; instead, it is the elastic component of the strain that is reduced. As the stress depends entirely on the elastic component of the strain, the stress also immediately begins to decrease. Hence, we do not travel back along the “outward” path, but instead return along a shifted version of the linear elastic region: the material exhibits hysteresis. Although the initial point and the final point of Figure 10B are both characterised by zero strain, the state is quite different, as the latter state has a large plastic strain. If we continue to reduce the strain, as in Figure 10C, the stress becomes negative - a compressive stress - until, once again, we reach the yield strength limit. Note that the yield strength in tension and the yield strength in compression are not necessarily equal.
In three dimensions, an elastoplastic material is characterised by a yield surface, which is the boundary of the elastic region. The yield surface is defined in stress space (or equivalently in strain space). For isotropic materials, the yield surface is most easily defined in the space of the three principal stresses. Stresses lying inside the yield surface are associated with an elastic state. When the stress reaches the yield surface, the material yields, and further increases in strain result in the stress state moving along the yield surface. Many different shapes of yield surface are possible, and are characteristic of different kinds of materials. Yield surfaces are conveniently defined mathematically by a yield function f, such that the yield surface is the locus of points for which f = 0. A complete explanation of elastoplastic behaviour in three dimensions is not given here. We recommend that you consult a good mechanics of materials textbook.
To specify an elastoplastic material, it is necessary both to specify its elastic
properties, and its plasticity. Currently Faim only allows plasticity to be defined with
isotropic elastic properties. A typical specification of an elastoplastic model using
n88modelgenerator will look something like this
n88modelgenerator --youngs_modulus=6829 --poissons_ratio=0.3 --plasticity=vonmises,50 mydata.aim
The currently supported plastic yield criteria are described below.
The von Mises yield criterion states that yielding begins when the distortional strain-energy density attains a certain limit. It is therefore also called the distortional energy density criterion. The distortional strain-energy density is the difference between the total strain energy density and the strain energy density arising only from the part of the strain resulting in a volume change. Hence, the distortional strain-energy density is associated with that part of the strain that results in no volume change: or, in other words, the part of the strain that causes a change in shape.
The yield function for a von Mises material, in terms of the three components of the principal stress, is given by
The parameter Y is the yield strength in uniaxial tension (or compression).
To specify a von Mises material in n88modelgenerator, use the parameter
plasticity. For example,
--plasticity=vonmises,68 will define a von Mises material with Y = 68.
The units of Y are the same as stress, so typically MPa.
The Mohr-Coulomb yield criterion is a refinement of the Tresca yield condition, which states that yielding begins when the shear stress at a point exceeds some limit. To this, the Mohr-Coulomb criterion adds a dependence on the hydrostatic stress, such that the shear stress limit is dependent on the hydrostatic stress, in particular that the shear stress limit increases with hydrostatic stress. The Mohr-Coulomb yield criterion is characterised by two values: the cohesion c and the angle of internal friction φ. For principal stresses in the order σ1 > σ2 > σ3, the Mohr-Coulomb yield function is
Under uniaxial tension, the yield strength is
while under uniaxial compression, the yield strength is
Mohr-Coulomb materials are specified to n88modelgenerator using these two
yield strengths. See plasticity. For example,
--plasticity=mohrcoulomb,40,80 will define a Mohr-Coulomb material with YT = 40
and YC = 80. The units of YT and YC are the same as stress, so typically MPa.
2.5.3. Material table generation
The parameter material_table allows one of two standard types of material table may be chosen: a simple table, consisting of a single material definition, or a Homminga material table, which relates density to stiffness.
If you require a material table different than either of the standard ones offered, you can use a material definitions file. See below for details.
The simplest material table consists of a single material definition. Thus it corresponds to homogeneous material properties: all elements are assigned the same material properties.
Note that although only a single material definition is created, it is nevertheless
still possible for the material table to have multiple entries corresponding to
multiple material IDs. In this case every material ID in the table maps of course to
the same single material definition. n88modelgenerator automates this: it examines
the segmented input image, and generates one entry in the material table for every
unique material ID (i.e. image value) present in the segmented image. Clearly, as a
matter of efficiency and simplicity, if you intend to use an image for analysis with
homogenous material properties, it is preferable to segment the image object to a
single material ID. It is not however, necessary to do so.
Homminga (2011) introduced a model that attempts to account for varying bone strength with density. In this model, the modulii vary according to the equation
Where ρ is the CT image density. For the orthotropic case, the shear modulii follow the same scaling, and for the anisotropic case, the stress-strain matrix follows this scaling.
To use this type of material table, the data must be segmented such that the material ID of each voxel is proportional to its CT image density. As material IDs are discrete, the CT image density is therefore binned. Hence
IDmax is set with the parameter homminga_maximum_material_id, and the exponent is set with the parameter homminga_modulus_exponent.
Emax will depend on the specified material. For an isotropic material, it will be given by youngs_modulus. However orthotropic or anisotropic materials may also be scaled: the entire stress-strain matrix scales according to the above-stated law.
|
|
In contrast to the homogenous material table, a Homminga material table is not
guaranteed a priori to have an entry for every material ID present in the input
segmented image. If your segmented image has material IDs larger than the specified
IDmax , n88modelgenerator will produce an error.
|
2.5.4. Material definitions file
The method presented up to this point for defining materials in
n88modelgenerator, while relatively easy, suffers from some limitations.
In particular, only a single material can be specified using the
options discussed so far. Furthermore, an anisotropic material can not
be specified at all using the command line parameters. n88modelgenerator
therefore provides an alternate method of defining materials, which is via
a material definitions file. A material definitions file can be used to
define any material known to Faim, any number of materials, and
any material table. A material definitions file can be specified with
the argument material_definitions.
The material definitions file format is straight-forward, as you can see from this example.
MaterialDefinitions:
CorticalBone:
Type: LinearIsotropic
E: 6829
nu: 0.3
TrabecularBone:
Type: LinearIsotropic
E: 7000
nu: 0.29
MaterialTable:
100: TrabecularBone
127: CorticalBone
Here we have a material definitions file containing two materials, both of which are linear elastic materials, but with different numerical values. Besides defining the materials, we have to specify the material table, which maps materials IDs (ie. the values present in the input image) to the materials we have defined.
|
|
The indenting in material definitions file is important, as it indicates how objects are grouped. Indenting must be done with spaces, and not with tabs. Technically, the material definitions file is in YAML format. Thus any valid YAML syntax can be used. In particular, it is possible to use curly brackets instead of indenting to indicate nesting, should you so wish. |
Here is another example material definitions file, which defines an anisotropic material.
MaterialDefinitions:
ExampleAnisoMat:
Type: LinearAnisotropic
StressStrainMatrix: [
1571.653, 540.033, 513.822, 7.53 , -121.22 , -57.959,
540.033, 2029.046, 469.974, 78.591, -53.69 , -50.673,
513.822, 469.974, 1803.998, 20.377, -57.014, -15.761,
7.53 , 78.591, 20.377, 734.405, -23.127, -36.557,
-121.22 , -53.69 , -57.014, -23.127, 627.396, 13.969,
-57.959, -50.673, -15.761, -36.557, 13.969, 745.749]
MaterialTable:
1: ExampleAnisoMat
The possible materials, and the values that must be specified for each, are listed in the following table.
| Type | Variable | Description |
|---|---|---|
LinearIsotropic |
|
Young’s modulus |
|
Poisson’s ratio |
|
LinearOrthotropic |
|
Young’s modulii as [Exx,Eyy,Ezz] |
|
Poisson’s ratios as [νyz,νzx,νxy] |
|
|
Shear modulii as [Gyz,Gzx,Gxy] |
|
LinearAnisotropic |
|
The 36 elements of the stress-strain matrix. Since the stress-strain matrix is symmetric, there are only 21 unique values, but all 36 must be given. They must be specified in the order K11 , K12 , K13, . . . K66 , but since the matrix is symmetric, this is equivalent to K11 , K21 , K31, . . . K66. |
VonMisesIsotropic |
|
Young’s modulus |
|
Poisson’s ratio |
|
|
Yield strength |
|
MohrCoulombIsotropic |
|
Young’s modulus |
|
Poisson’s ratio |
|
|
Mohr Coulomb c parameter (cohesion). |
|
|
Mohr Coulomb φ parameter (friction angle). |
|
|
Materials are stored in the n88model file using exactly the same
structure and variable names. See the
MaterialDefinitions group of
the n88model file specification.
|
3. Preparing Finite Element Models with vtkbone
You only need to read this chapter if you are interested in
writing scripts to create your own custom model types. For many users,
n88modelgenerator, as described in the previous chapter, will be sufficient.
Although n88modelgenerator can generate
many useful models for FE analysis, at times additional flexibility is
required. In order to provide as much flexibility to
the user as possible, we provide the option for users to perform custom
model generation. This functionality is provided by vtkbone toolkit,
which is built on
VTK . VTK is "an open-source, freely available software system
for 3D computer graphics, image processing and visualization", produced
by Kitware. VTK provides a great deal of functionality
to manipulate and visualize data that is useful for finite
element model generation and analysis. vtkbone is a collection of custom VTK
classes that extend VTK to add finite element pre-processing functionality.
The vtkbone library objects combined with generic VTK objects can be
quickly assembled into pipelines to produce nearly infinite customizability
for finite element model generation and post-processing analysis.
Basing vtkbone on VTK provides the following advantages.
- Large existing library of objects and filters
-
VTK is a large and well established system, with many useful algorithms already packaged as VTK objects.
- Built-in visualization
-
VTK was designed for rendering medical data. With it sophisticated visualizations are readily obtained. The visualization application ParaView is built with VTK and provides excellent complex data visualization.
vtkbonefunctionality is easily incorporated into ParaView. - Standardization
-
The time and effort the user invests in learning
vtkboneprovides familiarity with the widely-used VTK system, and is not limited in application to Numerics88 software. - Extensibility
-
The advanced user is able to write their own VTK classes where required.
- Multiple Language Support
-
VTK itself consists of C++ classes, but provides wrapping functionality to generate an interface layer to other languages.
vtkboneuses this wrapping functionality to provide a Python interface.
The best way to learn to use vtkbone is to follow the tutorials
in Tutorials.
We recommend that you use Python for assembling programs with vtkbone.
There are several advantages of using Python, including simplicity of
syntax and automatic memory management. In our experience,
writing programs using vtkbone in Python is far less time consuming, and
results in programs that are much easier to debug than writing the same
programs in C++ . This is particularly true for users without
significant programming experience.
|
|
Many of the tools provided with Faim are implemented as Python scripts.
Some use vtkbone, and some manipulate the n88model file directly through
the
python netCDF4 module, which is
installed automatically when you install n88tools. Examining
how these scripts work can be a good way to learn how to write your own custom
python scripts for manipulating Faim models.
|
3.1. vtkbone API documentation
The complete Application Programming Interface (API) reference documentation
for vtkbone is available at http://numerics88.com/documentation/vtkbone/1.0/ .
Class names in this document are linked to the vtkbone API documentation, so
that if you click on a class name, it should open
the documentation for that class. You should refer to the vtkbone API reference
documentation whenever using a vtkbone class, as the descriptions below are
introductory, and do not exhaustively cover all the functionality.
API documentation for VTK can be found at http://www.vtk.org/doc/release/6.3/html/ . Or you can get the latest version at https://vtk.org.download/ .
|
|
If you are using Python instead of C (and for most purposes, we
recommend that you do), then you will have to infer the Python interface
from the C interface. This is generally simple: class and method
names are the same, as are all positional argument names. Since Python is a
weakly-typed language, you do not need to be concerned generally with
the declared type of the arguments. A small number of C++ methods in
vtkbone do not have a Python equivalent, but this is rare.
|
3.2. Array indexing in vtkbone
Arrays in vtkbone, as in VTK, C and Python, are zero-indexed. That is, the
first element is element 0. This applies also to node numbers and element numbers.
(It does not however apply to material IDs, because the material ID is not an
array index; it is a key into a table look-up.) Be careful if reading an n88model file directly, because node numbers and element numbers are stored
1-indexed (see the file specification). The translation is done automatically
if you use the vtkbone objects vtkboneN88ModelReader and
vtkboneN88ModelWriter .
3.3. Typical workflow for vtkbone
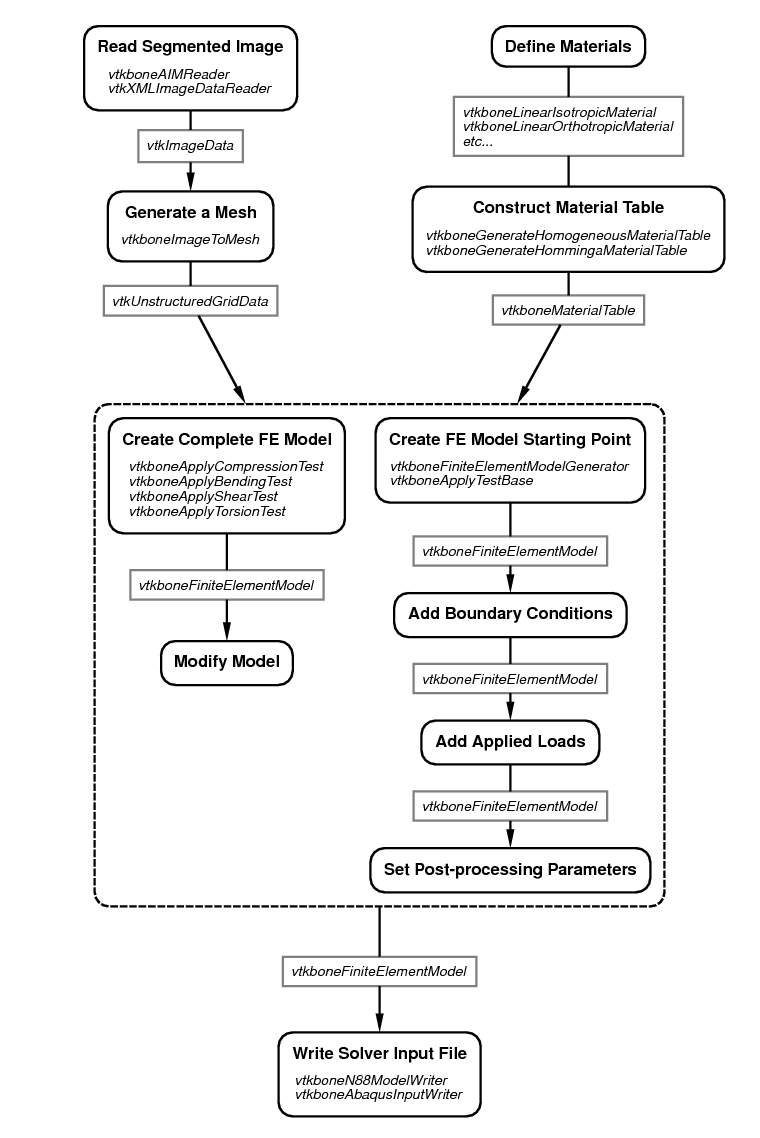
Figure 11 shows a typical work flow for creating a
finite element model using vtkbone. VTK generally consists of two
types of objects (or “classes”): objects that contain data, and objects that
process data. The latter are called “filters”. Filters can be chained
together to create a processing pipeline. In the figure, filters are
listed in the boxes with dark black lines and rounded corners; data
objects are listed in gray rectangles. The boxes with dark black lines and
rounded corners represent actions, and may list one or more VTK or
vtkbone objects that are suitable for performing the action.
The typical way to use a VTK filter object is to create it, set
parameters, set the input (if relevant), call Update(), and then get the
output. For example, for a vtkboneAIMReader object, which has an
output but no input, we might do this in Python
reader = vtkbone.vtkboneAIMReader()
reader.SetFileName ("MYFILE.AIM")
reader.Update()
image = reader.GetOutput()
|
|
There is an alternate way to use VTK filter objects, and that is to
chain them together in a pipeline. In this case, calling Update
on the last item in the pipeline will cause an update of all the
items in the pipeline, if required. To connect filters in a
processing pipeline, use reader = vtkbone.vtkboneAIMReader()
reader.SetFileName ("MYFILE.AIM")
mesher = vtkbone.vtkboneImageToMesh()
mesher.SetInputConnection (reader.GetOutputPort())
mesher.Update()
This automatically calls Update on the reader.
Generally, unless you have some application where the pipeline approach
is advantageous, we recommend the simpler method of using |
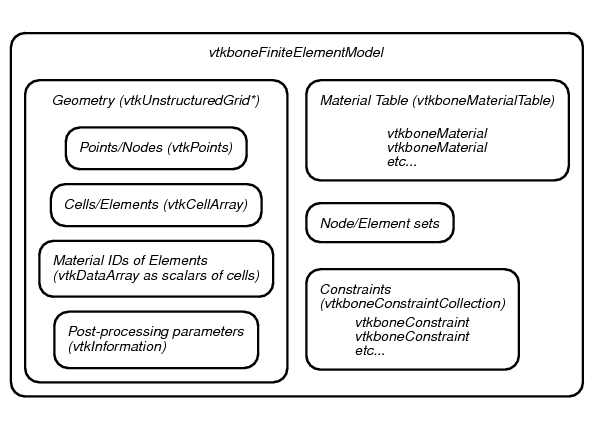
3.4. The vtkboneFiniteElementModel object
The central class that vtkbone adds to VTK is a new type of data class, called
vtkboneFiniteElementModel . The conceptual structure of vtkboneFiniteElementModel
is shown in Figure 12.
vtkboneFiniteElementModel is a subclass of
the VTK class vtkUnstructuredGrid , which represents a data set as consisting of an
assortment of geometric shapes. In VTK terminology, these individual shapes
are “Cells”. They map naturally to the concept of Elements in finite element
analysis. The vertices of the cells, in VTK terminology, are “Points”. These
are equivalent to Nodes in finite element analysis. vtkUnstructuredGrid , like other VTK
objects, is capable of storing specific types of additional information, such
as one or more scalar or vector values associated with each Cell or Point.
This aspect is used for storing, for example, material IDs, which are mapped
to the scalar values of the Cells. To
vtkUnstructuredGrid , vtkboneFiniteElementModel adds some additional
information related to requirements for finite element analysis such as material properties and
constraints (i.e. displacement boundary conditions and applied loads), as well as
sets of Points and/or Cells, which are useful for defining constraints and
in post-processing. Sets and constraints are indexed by an assigned name, which is convenient
for accessing and modifying them.
3.5. Reading a segmented image
We typically read in data as a segmented 3D volumetric image from micro-CT. The image values (i.e. the pixel or voxel values) need to correspond to the segmented material IDs. The selection of a file reading object will be appropriate to the input file format. The output of the file reader filter will be a vtkImageData object.
We have already given the example of using a vtkboneAIMReader to read a Scanco AIM file, which was
reader = vtkbone.vtkboneAIMReader()
reader.SetFileName ("MYFILE.AIM")
reader.Update()
image = reader.GetOutput()
|
|
One slightly obscure technical issue which may arise is: are the data
of a vtkImageData associated with the Points or the Cells? Either is possible in
VTK. The scalar image data (scalar because there is one value per location)
must be explicitly associated either with the Cells or with the Points.
(In fact it’s possible to have different scalar data on the Cells and the
Points.) Thinking about it as an FE problem, it is natural to associate
the image data with Cells, where each image voxel becomes an FE element. Thus,
we like to think of each value in the image as being at the center of
a Cell in the VTK scheme. VTK however has generally standardized
on the convention of image data being on the Points. There are some important
consequences. For example, a vtkImageData that has dimensions of
(M,N,P) has (M,N,P) Points, but only (M-1,N-1,P-1) Cells. Or conversely, if you
have data with dimensions of (R,S,T), and you
want to put the data on the Cells, then you actually require a vtkImageData
with dimensions of (R+1,S+1,T+1). Also, if the origin is important, one
needs to keep in mind that the origin is the location of the zero-indexed
Point. In terms of the Cells, this is the “lower-left” corner of the
zero-indexed Cell, not the center of that Cell. vtkbone objects that
require images as input will accept input with data either on the points
or on the Cells. However, many VTK objects that process
images work correctly only with input data on the Points. By contrast, if you
want to render the data and color according to the scalar image, the rendering
is quite different depending on whether the scalar data is on the Points or the Cells.
Generally, you get the expected result in this case by putting the data on the
Cells. This discussion is important because it illustrates that there is no
one universally correct answer to whether image data belongs on
the Points or on the Cells. vtkbone image readers, such as
vtkboneAIMReader have an option DataOnCells to control the desired
behaviour. VTK image readers always put image data on the Points, so if
you need the data on the Cells, you must to copy the output to a new vtkImageData .
|
Examples of reading data with vtkbone are given in the tutorials Compressing a cube revisited using vtkbone and Advanced custom model tutorial: a screw pull-out test.
3.6. Reading an unsegmented image and segmenting it
If you have an unsegmented image such as a raw micro-CT image that
has scalar values still in terms of density, it is possible to process the image with
VTK. Segmentation is a complex subject, which we are unable to cover
here. For an
example of a simple segmentation, where only a density threshold
and connectivity are considered, consult the example in the directory
examples/segment_dicom.
3.7. Ensuring connectivity
A well-defined problem for finite element analysis requires that all parts of the object in the image be connected as a single object.
Disconnected parts in the input create an ill-defined problem, with
an infinite number of solutions. These arise, for example, when there
is noise in the image data. Some solvers cannot solve this kind of problem
at all (the global stiffness matrix is singular). n88solver will typically
find a solution. However, the convergence might be very slow as it attempts
to find the non-existent optimum position for the disconnected
part.
To avoid this problem, the input image can be processed with the filter ImageConnectivityFilter . This filter has many options and different modes of operation, but in most cases the default mode is sufficient. In the default behaviour:
-
Zero-valued voxels are considered “empty space”, and no connection is possible though them.
-
Voxels are considered connected if they share a face. Sharing only a corner or an edge is not sufficient.
-
Only the largest connected object in the input image is passed to the output image. Smaller objects that have no continuous path of connection to the largest connected object are zeroed-out.
Because of the first point, it is clearly necessary to segment the image before applying ImageConnectivityFilter , because empty space must be labelled with the value 0.
connectivity_filter = vtkbone.vtkboneImageConnectivityFilter() connectivity_filter.SetInput (image) connectivity_filter.Update() image = connectivity_filter.GetOutput()
Notice that we use the variable name image for both the input
and the output. This causes no problems in Python, although by doing this we can no longer
use this to refer to the input image as the second call to image reassigns
the variable the value of connectivity_filter.GetOutput(). If it were necessary to refer
to the input image, then we should use different names for the input and output. |
If your input image is processed and segmented with another software package, it is still a good idea to verify the connectivity of the input image. If your input image is carefully prepared, and you don’t want to inadvertently modify it, you can check for connectivity without modifying it like this:
connectivity_mapper = vtkbone.vtkboneImageConnectivityMap()
connectivity_mapper.SetInput (image)
connectivity_mapper.Update()
if connectivity_mapper.GetNumberOfRegions() != 1:
print "WARNING: Input image does not consist of a single connected object."
Examples of ensuring connectivity are given in the tutorials Compressing a cube revisited using vtkbone and Advanced custom model tutorial: a screw pull-out test.
3.8. Generating a mesh
Once we have a segmented and connected image, we convert the image to a mesh of elements, represented by
a vtkUnstructuredGrid object. The base class vtkUnstructuredGrid supports many
types of Cells, but currently vtkbone supports only VTK_HEXAHEDRON and VTK_VOXEL. The topology of VTK_VOXEL is shown in Figure 13.
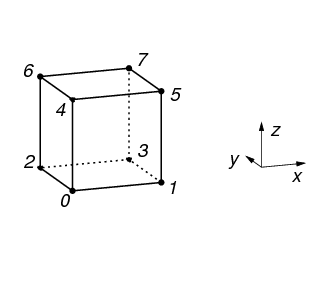
Generating a mesh in vtkbone is straightforward; simply pass the input image
to a vtkboneImageToMesh filter. It takes no options; the important choices
were made already during the segmentation stage. In Python this looks
like this
mesher = vtkbone.vtkboneImageToMesh() mesher.SetInput (image) mesher.Update() mesh = mesher.GetOutput()
vtkboneImageToMesh creates one Cell (i.e. element) of type VTK_VOXEL for every
voxel in the input image that has non-zero scalar value. The scalar values of
the image become the scalar values of the output Cells. It also creates Points
at the vertices (corners) of the Cells. There are no duplicate Points:
neighbouring Cells will reference the same Point on shared vertices.
|
|
Cells and Points in VTK are ordered; they can be indexed by
consecutive Cell or Point number. This ordering is not inconsequential.
In Faim, the solver efficiency is optimal with certain orderings, and in fact
there are orderings for which the solver fails with an error message.
The ordering output by vtkboneImageToMesh is
“x fastest, z slowest”. It is recommended to always preserve this ordering.
|
3.9. Defining materials
Material definitions are generated by creating a instance of a class of the
corresponding material type, and then calling the appropriate methods to set
the material parameters. Every material must have a unique name. vtkbone will
assign default unique names when defining a new material object, but
the names will be more meaningful if you assign them yourself.
vtkbone version 9 supports the following material classes:
Plus special material classes that are in fact material arrays, which are discussed below.
Here is an example of creating a simple linear isotropic material:
linear_material = vtkbone.vtkboneLinearIsotropicMaterial() linear_material.SetYoungsModulus (800)linear_material.SetPoissonsRatio (0.33) linear_material.SetName ("Linear 800")
| As discussed in A note about units, the units of Young’s modulus depend on the input length units. If the length units are mm and force units in N, then Young’s modulus has units of MPa. |
This is the construction of a Mohr-Coulomb elastoplastic material:
ep_material = vtkbone.vtkboneMohrCoulombIsotropicMaterial() ep_material.SetYoungsModulus (800) ep_material.SetPoissonsRatio (0.33) ep_material.SetYieldStrengths (20, 40)ep_material.SetName ("Mohr Coulomb material 1")
| For Mohr-Coulomb, this pair of numbers is the yield strength in tension and the yield strength in compression. The units of yield strength are the same as stress, so typically MPa. |
In addition to the standard material classes, there are material array classes. Simply put, these define not a single material, but a sequence of similar materials with variable parameters. For a discussion of the circumstances in which this could be useful, see Efficient Handling of Large Numbers of Material Definitions. The material array classes do inherit themselves from vtkboneMaterial (rather than being a collection of vtkboneMaterial objects). They can therefore be used nearly anywhere that a regular material can be; in particular, they can be inserted as entries into a material table. The material array classes are
3.10. Constructing a material table
Once you have created your material definitions, you need to combine them into a material table, which maps material IDs to the material definitions.
For example, if we want a homogenous material, and the input image has only the scalar value 127 for bone (and 0 for background), then we can make a material table like this:
materialTable = vtkbone.vtkboneMaterialTable() materialTable.AddMaterial (127, linear_material)
We created the material linear_material above. |
We must assign a material for every segmentation value present in the input.
The same material can be assigned to multiple material IDs.
For example, suppose the input image has segmentation values 100-103, and
we have created two different materials, materialA and materialB,
then we could create a vtkboneMaterialTable like this:
materialTable = vtkbone.vtkboneMaterialTable() materialTable.AddMaterial (100, materialA) materialTable.AddMaterial (101, materialB) materialTable.AddMaterial (102, materialB) materialTable.AddMaterial (103, materialB)
There are a couple of helper classes that simplify the creation of material tables for common cases. For a model with a homogenous material, we can use vtkboneGenerateHomogeneousMaterialTable . This class assigns a specified vtkboneMaterial to all the scalar values present in the input mesh. The size of the resulting material table depends on the number of distinct input values. For example,
mtGenerator = vtkbone.vtkboneGenerateHomogeneousMaterialTable() mtGenerator.SetMaterial (material1) mtGenerator.SetMaterialIdList (mesh.GetCellData().GetScalars()) mtGenerator.Update() materialTable = mtGenerator.GetOutput()
We could alternatively set SetMaterialIdList with the scalars from the image, rather than those of the mesh; the results will be the same.
Another useful helper class is vtkboneGenerateHommingaMaterialTable . Refer to the the section on the Homminga material model in the chapter on preparing models with n88modelgenerator.
Examples of defining materials and creating a material table are given in the tutorials Compressing a cube revisited using vtkbone, Deflection of a cantilevered beam: adding custom boundary conditions and loads and Advanced custom model tutorial: a screw pull-out test.
3.11. Creating a finite element model
At this stage, we combine the geometric mesh with the material table to create a vtkboneFiniteElementModel object. The most elementary way to do this is with a vtkboneFiniteElementModelGenerator , which can be used like this
modelGenerator = vtkbone.vtkboneFiniteElementModelGenerator() modelGenerator.SetInput (0, mesh) modelGenerator.SetInput (1, materialTable) modelGenerator.Update() model = modelGenerator.GetOutput()
After combining the mesh with the material table, all that is now required to
make a complete finite element model is to add boundary conditions and/or
applied loads, and to specify node and element sets for the post-processing.
For standard tests,
there are vtkbone filters to generate complete models, and these are
described below in Filters for creating standard tests.
3.12. Creating node and element sets
Before we can create boundary conditions or applied loads, we need to define node and/or element sets that specify all the nodes (or elements) to which we want to apply the boundary condition (displacement or applied load). Node and element sets are also used during post-processing. This will be discussed later in Setting post processing parameters.
Any number of node and element sets may be defined. They must be named, and they are accessed by name. The node and element sets are simply lists of node or element numbers, and are stored as vtkIdTypeArray . There are many ways to create node and element sets. A very simple way is to simply enumerate the node numbers (or element numbers). For example, if we wanted to create a node set of the nodes 8,9,10,11 , this would be the code:
nodes = array ([8,9,10,11]) nodes_vtk = numpy_to_vtk (nodes, deep=1, array_type=vtk.VTK_ID_TYPE)nodes_vtk.SetName ("example_node_set") model.AddNodeSet (nodes_vtk)
In Python, the most flexible way to handle array data is with
numpy arrays, however the data must be passed to VTK objects as
vtkDataArray . numpy_to_vtk does the conversion. |
VTK offers many ways to select Points and Cells, for example by geometric criteria.
As an example of this, refer to the screw_pullout_tutorial where a node set
is selected from nodes located on a particular rough surface, and subject to additional
criterion r1 < r < r2 , where r is the radius from a screw axis.
vtkbone also offers some utility functions for identifying node and elements
sets. These can be found in vtkboneSelectionUtilities .
Frequently, we require sets corresponding to the faces of the model (i.e. the boundaries of the image). In this case, we may use the class vtkboneApplyTestBase . vtkboneApplyTestBase is a subclass of vtkboneFiniteElementModelGenerator , with the extra functionality of creating pre-defined sets. vtkboneApplyTestBase implements the concept of a Test Frame and a Data Frame. Refer to test orientation in the chapter on n88modelgenerator. vtkboneApplyTestBase creates the node and element sets given in the following table. Note that in each case there is both a node and element set, with the same name.
| Set name | Consists of |
|---|---|
face_z0 |
nodes/elements on the bottom surface (z=zmin) in the Test Frame. |
face_z1 |
nodes/elements on the top surface (z=zmax) in the Test Frame. |
face_x0 |
nodes/elements on the x=xmin surface in Test Frame. |
face_x1 |
nodes/elements on the x=xmax surface in Test Frame. |
face_y0 |
nodes/elements on the y=ymin surface in Test Frame. |
face_y1 |
nodes/elements on the y=ymax surface in Test Frame. |
The sets “face_z0” and “face_z1” are of particular importance, as the standard tests are applied along the z axis in the Test Frame.
vtkboneApplyTestBase has options UnevenTopSurface()
and UnevenBottomSurface() by which we can choose to have “face_z0” and/or “face_z1”
as the set of nodes/elements on an uneven surface, instead of the boundary of the
model. This is especially useful when the object in the image does not
intersect the top/bottom boundaries
of the image. See further discussion on uneven surfaces in
the chapter on n88modelgenerator. The two sets “face_z0” and “face_z1” can also be limited to
a specific material, as defined by material ID.
vtkboneApplyTestBase is used identically to vtkboneFiniteElementModelGenerator , except that additional optional settings may be set if desired. For example, here we define a model with a test axis in the y direction, and specify that we want the set “face_z1” to be the uneven surface in the image, where we are limiting the search for the uneven surface to a maximum distance of 0.5 from the image boundary.
modelGenerator = vtkbone.vtkboneApplyTestBase() modelGenerator.SetInput (0, mesh) modelGenerator.SetInput (1, materialTable) modelGenerator.SetTestAxis (vtkbone.vtkboneApplyTestBase.TEST_AXIS_Y) modelGenerator.UnevenTopSurfaceOn() modelGenerator.UseTopSurfaceMaximumDepthOn() modelGenerator.SetTopSurfaceMaximumDepth (0.5) modelGenerator.Update() model = modelGenerator.GetOutput()
An example of using the standard node and element sets from vtkboneApplyTestBase is given in Deflection of a cantilevered beam: adding custom boundary conditions and loads. The tutorial Advanced custom model tutorial: a screw pull-out test demonstrates a sophisticated selection of custom node sets.
3.13. Adding boundary conditions
Once we have created the node sets, creating a boundary condition applied
to the nodes of a particular node set is straightforward and can be done
with the method ApplyBoundaryCondition() of vtkboneFiniteElementModel . For example,
to fix the bottom nodes and apply a displacement of 0.1 to the top nodes,
we could do this
model.ApplyBoundaryCondition (
"face_z0",
vtkbone.vtkboneConstraint.SENSE_Z,  0,
"bottom_fixed")
0,
"bottom_fixed")  model.ApplyBoundaryCondition (
"face_z1",
vtkbone.vtkboneConstraint.SENSE_Z,
-0.1,
model.ApplyBoundaryCondition (
"face_z1",
vtkbone.vtkboneConstraint.SENSE_Z,
-0.1,  "bottom_fixed")
"bottom_fixed")
vtkbone.vtkboneConstraint.SENSE_Z has the value 2 (see vtkboneConstraint ). It is possible
just to use that value 2 here, but SENSE_Z is more informative. |
|
| This is the user-defined name assigned to the boundary condition. Every constraint must have a unique name. | |
| Negative if we want compression. |
The “sense” is the axis direction along which the displacement is applied.
The other axis directions remain free unless you also specify a value for
them. It is quite possible, and common, to call ApplyBoundaryCondition()
three times on the same node set, once for each sense.
ApplyBoundaryCondition() can take different types of arguments, for example
arrays of senses, displacements and node numbers. Refer to the API documentation
for vtkboneFiniteElementModel . There is also a convenience method
FixNodes(), which is a quick way to set all senses to a zero displacement.
Boundary conditions are implemented within vtkboneFiniteElementModel as a specific type of vtkboneConstraint . All the constraints associated with a vtkboneFiniteElementModel are contained in a vtkboneConstraintCollection . It is possible to modify either vtkboneConstraintCollection or a particular vtkboneConstraint manually. For example, we could create a boundary condition on two nodes in the following manner. This is somewhat laborious and usually unnecessary, but it can be adapted to create unusual boundary conditions.
node_ids = array([3,5])
node_ids_vtk = numpy_to_vtk (node_ids, deep=1, array_type=vtk.VTK_ID_TYPE)
senses = array ([0,2]) # x-axis, z-axis
senses_vtk = numpy_to_vtk (senses, deep=1, array_type=vtk.VTK_ID_TYPE)
senses_vtk.SetName ("SENSE")
values = array([0.1,0.1])
values_vtk = numpy_to_vtk (values, deep=1, array_type=vtk.VTK_ID_TYPE)
values_vtk.SetName ("VALUE")
constraint = vtkbone.vtkboneConstraint()
constraint.SetName ("a_custom_boundary_condition")
constraint.SetIndices (node_ids)
constraint.SetConstraintType (vtkbone.vtkboneConstraint::DISPLACEMENT)
constraint.SetConstraintAppliedTo (vtkbone.vtkboneConstraint::NODES)
constraint.GetAttributes().AddArray (senses)
constraint.GetAttributes().AddArray (values)
model.GetConstraints().AddItem (constraint)
Examples of applying boundary conditions are given in the tutorials Deflection of a cantilevered beam: adding custom boundary conditions and loads and Advanced custom model tutorial: a screw pull-out test.
3.14. Adding applied loads
Creating an applied load is similar to creating a displacement boundary
condition. They are both implemented as vtkboneConstraint . However, while displacement
boundary conditions are applied to nodes, applied loads are applied to elements; in fact they are applied to a particular
face of an element (or to the body of an element).
Therefore, the ApplyLoad() method of
vtkboneFiniteElementModel takes the name of an element set, and
has an additional input argument which specifies to which faces of the
elements the load is applied. Here is an example of creating an
applied load on the top surface of the model:
model.ApplyLoad (
"face_z1",  vtkbone.vtkboneConstraint.FACE_Z1_DISTRIBUTION,
vtkbone.vtkboneConstraint.SENSE_Z,
vtkbone.vtkboneConstraint.FACE_Z1_DISTRIBUTION,
vtkbone.vtkboneConstraint.SENSE_Z,  6900,
6900,  "bottom_fixed")
"bottom_fixed")
| Refers to the element set “face_z1”, not the corresponding node set, which very often also exists with the same name. | |
| In this example, the applied force is perpendicular to the specified element face, but it is not required to be so. | |
| This is the total load applied. The load is evenly distributed between all of the element faces. |
To apply forces along non-axis directions, call ApplyLoad() multiple times
with different senses.
As with displacement boundary conditions, we can create an applied force manually, if we require more flexibility. It will look something like this:
element_ids = array([3,5])
element_ids_vtk = numpy_to_vtk (element_ids, deep=1, array_type=vtk.VTK_ID_TYPE)
distributions = ones ((2,)) * vtkbone.vtkboneConstraint.FACE_Z1_DISTRIBUTION
distributions_vtk = numpy_to_vtk (distributions, deep=1, array_type=vtk.VTK_ID_TYPE)
distributions_vtk.SetName ("DISTRIBUTION")
senses = array ([0,2]) # x-axis, z-axis
senses_vtk = numpy_to_vtk (senses, deep=1, array_type=vtk.VTK_ID_TYPE)
senses_vtk.SetName ("SENSE")
total_load = 6900
values = total_load * ones(2, float) / 2
values_vtk = numpy_to_vtk (values, deep=1, array_type=vtk.VTK_ID_TYPE)
values_vtk.SetName ("VALUE")
constraint = vtkbone.vtkboneConstraint()
constraint.SetName ("a_custom_applied_load")
constraint.SetIndices (element_ids)
constraint.SetConstraintType (vtkbone.vtkboneConstraint::FORCE)
constraint.SetConstraintAppliedTo (vtkbone.vtkboneConstraint::ELEMENTS)
constraint.GetAttributes().AddArray (distributions)
constraint.GetAttributes().AddArray (senses)
constraint.GetAttributes().AddArray (values)
model.GetConstraints().AddItem (constraint)
|
|
You can apply loads to nodes instead of to elements if you desire. You must create a constraint by hand to do this, as there is no convenience method provided for this purpose. This is most sensible when you desire to apply a point force (i.e. to a single node). Be careful about applying forces to nodes because applying a constant force to each of a set of nodes on a surface is not equivalent to applying a uniform pressure to that surface. By contrast, applying a constant force to a set of element faces is equivalent to a uniform pressure, which is why it is usually more convenient to define loads on element faces. |
|
|
Applied loads are additive. That is, if you create more than one applied load on a particular element face, the loads will add. Displacement boundary conditions by contrast are unique. If you create more than one displacement boundary condition applying to a particular node and sense, then only one of them will be used by the solver, and the other will be discarded. Which of multiple boundary conditions applying to the same degree of freedom is used is indeterminate, so it is a logical error to create multiple different boundary conditions applying to the same degree of freedom. No warning or error message will be generated in the case of multiple boundary conditions on the same degree of freedom. (It is sometimes convenient to be able to do so in cases where the actual value used turns out not to matter). |
An example of adding an applied load is given in the tutorial Deflection of a cantilevered beam: adding custom boundary conditions and loads.
3.15. Optional: Adding a convergence set
Adding a convergence set is optional, but it allows the solver to use the convergence set convergence measure, which is generally the best one for linear models. Best in this context means that the solver can reliably identify when a certain precision has been obtained, and thus stop iterating. Less tailored convergence measures, which don’t require the definition of a convergence set, must be more conservative, and thus run to more iterations to be certain of obtaining a given precision. See Convergence measure.
Convergence sets are most conveniently defined with the method ConvergenceSetFromConstraint
of vtkboneFiniteElementModel. You simply pass it the most relevant
boundary condition or applied force. “Most relevant” simply means the one
you are most interested in.
For example, the standard compression tests generate their convergence sets with
model.ConvergenceSetFromConstraint("top_displacement")
Here top_displacement is the name of the boundary condition on the top surface. This results in a convergence set which is equivalent to the total force on the top surface.
In Tutorial: Deflection of a cantilevered beam; adding custom boundary conditions and loads, an applied force is defined on the tip of a cantilever, and the convergence set is generated with
model.ConvergenceSetFromConstraint("end_force")
This results in a convergence set which is the average displacement of the tip of the cantilever.
However defined, if convergence set is used as the convergence measure, then the solver watches that quantity to determine when it has ceased to change meaningfully, and thus, when iterating can be stopped.
|
|
You cannot define a convergence set that consists entirely of fixed nodes. That is, entirely of boundary condition nodes that are set to zero displacement. This is because the solver internally elimates these degrees of freedom, and is hence unable to calculate the corresponding forces during iterations. |
3.16. Ensuring your model is well-defined
It is possible to create a model that is degenerate, or not well-defined. In other words, a model that has not a single solution, but many solutions (typically an infinite number). As a linear algebra problem, such a problem has a singular global stiffness matrix. For example, consider the standard uniaxial problem where a sample volume is compressed between two hard parallel plates. (See uniaxial test in the chapter on n88modelgenerator). If we specify no contact friction, then although the sample compresses in a predictable way between the two plates, it is free to slide around as a whole (translate) anywhere between the plates. For the particular case of the uniaxial model, n88modelgenerator provides the option to add a pin, which consists of the following additional constraints:
-
fix the x,y senses of an arbitrary node, and
-
fix one sense of another node (usually from the same element).
The first constraint is sufficient to prevent translation, and the second constraint is required to prevent rotation.
Models with only applied loads and no displacement boundary conditions are always ill-defined.
Practically, n88solver will usually solve even ill-defined problems. In
fact, for the type of ill-defined problem described here,
it often does so faster than the equivalent well-defined problem (i.e.
one with added “pin” constraints to make it non-singular). Many types
of ill-defined problems can cause n88solver to converge much more slowly. For example,
see the discussion on Ensuring connectivity.
Not all solvers
however can handle ill-defined problems, so this should be avoided when
exporting models to other solvers. Also, if you would like overlay
the renderings of two similar ill-defined problems or compare differences
in any way, it is usually necessary to first register them to eliminate
meaningless differences (such as overall translations or rotations in
the example described).
3.17. Setting post-processing parameters
If you have followed every step, then you have a model that is completely defined for the solver. In fact you could save it to a file and solve it now. The post-processor n88postfaim however requires a bit more information so that meaningful results can be extracted from the solved model. n88postfaim calculates certain quantities with reference to node or element sets. For example, in a compression test the relevant sets correspond to the top and bottom faces, as we are interested principally in the forces on these faces. These sets already exist (“face_z0” and “face_z1”), as we previously used them to apply boundary conditions. We need to list the relevant node sets to be used by n88postfaim. Of course, if you’re doing some custom post-processing that does not involve n88postfaim, then this step is optional and can be skipped. Setting the post-processing node sets involves setting some “information” with a key (this may seem slightly obscure, but it is a standard VTK technique):
info = model.GetInformation() pp_node_sets_key = vtkbone.vtkboneSolverParameters.POST_PROCESSING_NODE_SETS() pp_node_sets_key.Append (info, "face_z0") pp_node_sets_key.Append (info, "face_z1")
Any number of sets may be specified for post-processing. n88postfaim requires the element sets as well as the node sets, and they must match exactly, meaning that the nth post-processing element set must be exactly those elements which contain any of the nodes of the nth post-processing node set. (The element set name is not required to be the same as the node set name).
If you’ve used vtkboneApplyTestBase to get pre-defined node and element sets, then you already have the corresponding element sets, and in fact they have the same names, so
info = model.GetInformation() pp_node_sets_key = vtkbone.vtkboneSolverParameters.POST_PROCESSING_NODE_SETS() pp_node_sets_key.Append (info, "face_z0") pp_node_sets_key.Append (info, "face_z1") pp_elem_sets_key = vtkbone.vtkboneSolverParameters.POST_PROCESSING_ELEMENT_SETS() pp_element_sets_key.Append (info, "face_z0") pp_element_sets_key.Append (info, "face_z1")
If you’ve created custom node sets, then you can obtain the corresponding
element sets with the method GetAssociatedElementsFromNodeSet(), so
for example (taken from the screw pull-out tutorial),
info = model.GetInformation()
pp_node_sets_key = vtkbone.vtkboneSolverParameters.POST_PROCESSING_NODE_SETS()
pp_elem_sets_key = vtkbone.vtkboneSolverParameters.POST_PROCESSING_ELEMENT_SETS()
for setname in ["bone_top_visible", "screw_top"]:
pp_node_sets_key.Append (info, setname)
elementSet = model.GetAssociatedElementsFromNodeSet (setname)
model.AddElementSet (elementSet)
pp_elem_sets_key.Append (info, setname)
Examples of setting post-processing parameters are given in the tutorials Deflection of a cantilevered beam: adding custom boundary conditions and loads and Advanced custom model tutorial: a screw pull-out test.
3.18. Filters for creating standard tests
For each of the standard tests, namely the ones that n88modelgenerator can generate, there is a filter to generate the test, complete with all displacement boundary conditions, applied forces, and relevant post-processing sets. Of course, it is easier to just simply use n88modelgenerator for these cases rather than write a script. However, these filters provide more options than are exposed by n88modelgenerator, and a script will allow you to access these options. Furthermore, sometimes a standard model is nearly, but not quite, what you want. In this case, the fastest way to proceed is to use a standard test generating filter, and then tweak the resulting model.
All the standard test filters are subclasses of vtkboneApplyTestBase (see Creating node and element sets), so that they support variable orientation as defined by the Data Frame and the Test Frame, as well as having the standard sets defined (“face_z0”, etc…)
The following table lists the standard model filters.
| vtkbone filter | n88modelgenerator test types |
|---|---|
For details on the options supported by these filters, refer to the API documentation.
An example of using a standard test filter is given in the tutorial Compressing a cube revisited using vtkbone.
3.19. Modifying a finite element model
Often a standard model type will be very close to the desired test configuration, but some modifications are needed. Every part of vtkboneFiniteElementModel can be modified, or even deleted, after creation. There are in general too many possibilities to enumerate here.
If a model is already written as an n88model file, it can be read with
vtkboneN88ModelReader , modified, and rewritten.
3.20. Updating the history and the log
It is good practice (but not strictly necessary) to add relevant
details to the History and Log fields of a model before writing
it out. This will assist greatly in the future if it is required to
trace back the origins and history of a given
n88model file.
The history and comments of an n88model file can be viewed
with the command
n88modelinfo --history --comments myfile.n88model
You can leave out the --history and --comments arguments, although
then you will get a lot more information about the model, possibly more
than you want.
The History field should have one line per executable that modifies the
model file. This line should start with a time/date stamp and briefly state
the program (and perhaps the user) which modified or created the file.
History can be added with the method AppendHistory(); the date/time
stamp will be automatically added. For example
model.AppendHistory("Created with screwpullout.py version 6.0")
The Log field is intended to record any other information that would
be useful to be able to recover at a later time. Every addition can be any number of lines long. You should
record any parameters or settings that are relevant here. As for
AppendHistory(), AppendLog() will add a date/time stamp (although
on its own line). It will also ensure that every addition to the Log
is separated by a black line from other additions to Log, for ease in
reading it. For example
settingsText = ["Configuration:",
"input file = %s" % input_image_file,
"output file = %s" % output_faim_file,
"bone material id = %s" % bone_material_id,
"bone material Young's modulus = %s" % bone_material_modulus,
"bone material Poisson's ratio = %s" % bone_material_poissons_ratio,
"screw material id = %s" % screw_material_id,
"screw material Young's modulus = %s" % screw_material_modulus,
"screw material Poisson's ratio = %s" % screw_material_poissons_ratio,
"screw displacement = %s" % screw_displacement,
"inner ring radius = %s" % inner_ring_radius,
"bone constraint max depth = %s" % bone_constraint_max_depth]
model.AppendLog ("\n".join(settingsText)) 
This might look pretty weird if you’re not a Python guru. settingsText
is a Python list of strings (each of one line). "\n".join(settingsText)
joins them all into one long string, separated by line returns. |
|
|
A particularly clever trick if your script uses a configuration file to set values, one which is used by n88modelgenerator, and also used in the above example (which is from the screw pull-out tutorial), is to write the settings into the Comment field in exactly the same format that they appear in the configuration file. Then, if ever the data need to be exactly re-created for some reason, the settings can be copied from the Log and pasted directly into a new configuration file. The script can then be rerun with that configuration file without any further editing. |
Examples of adding information to the history and to the log are given in the tutorials Compressing a cube revisited using vtkbone, Deflection of a cantilevered beam: adding custom boundary conditions and loads and Advanced custom model tutorial: a screw pull-out test.
3.21. Writing a model file for input to the solver
When your vtkboneFiniteElementModel is the way you like it, writing a file is straightforward:
writer = vtkbone.vtkboneN88ModelWriter()
writer.SetInput (model)
writer.SetFileName ("a_snazzy_model.n88model")
writer.Update()
Other formats can also be written using the appropriate writer including,
3.22. Visualizing intermediate results
When developing a complicated model, it is often a good idea to write out intermediate results that can be visualized. This can be done either by writing out intermediate geometries and node sets using standard VTK file format writers, such as vtkXMLUnstructuredGridWriter and vtkXMLPolyDataWriter , or by writing the model with vtkboneN88ModelWriter as early as possible as you build up your script, before the model is complete. Even incomplete models can be visualized. The tool n88extractsets is handy to extract and visualize node and element sets, as well as boundary conditions and applied loads.
For an example of visualizing intermediate results as the model is built up, see Advanced custom model tutorial: a screw pull-out test.
3.23. Error handling
VTK classes do not throw exceptions or halt execution when an error occurs. If catching error conditions is important to you, you need to provide a VTK observer class. For more information, refer to http://www.vtk.org/Wiki/VTK/Tutorials/Callbacks . However, if you don’t provide an error observer (and most often, you won’t want to be bothered to), you will still be informed about error conditions by a message printed to standard out (i.e. to the console). For scripting purposes, this is generally adequate.
If you do want to trap the error, here is an example in Python.
class ErrorObserver:
def __init__(self):
self.__ErrorOccurred = False
self.__ErrorMessage = None
self.CallDataType = 'string0'
def __call__(self, obj, event, message):
self.__ErrorOccurred = True
self.__ErrorMessage = message
def ErrorOccurred(self):
occ = self.__ErrorOccurred
self.__ErrorOccurred = False
return occ
def ErrorMessage(self):
return self.__ErrorMessage
errorObserver = ErrorObserver()
reader = vtkbone.vtkboneN88ModelReader()
reader.AddObserver ("ErrorEvent", errorObserver)
reader.SetFileName (filename)
reader.Update()
if errorObserver.ErrorOccurred():
print "ERROR reading file: ", errorObserver.ErrorMessage()
sys.exit (-1)
vtkbone provides a very simple error observer class, vtkboneErrorWarningObserver . Its use however is limited to C++ code; use the above example for Python.
4. Solving Linear Problems
4.1. Obtaining solutions to linear problems using n88solver_slt
For a model with only linear elastic materials, the solver can be run as follows
n88solver_slt myfile.n88model
In special cases, you may want to use n88solver_sla instead of n88solver_slt:
See Efficient Handling of Large Numbers of Material Definitions.
Everything in this section applies equally well to that solver.
The solution as expressed as displacements - from the original position - at node.
The displacements are written into the input file; no additional output
file is created. If the n88model file contains an existing solution, it
will be overwritten. Furthermore, if there is an existing solution, it will be used as a
starting point for the solver for further iterations. This behaviour is not always desired
and can be suppressed; see restart for details.
|
|
To check whether an n88modelinfo --history --solutions myfile.n88model See n88modelinfo for more details. |
The complete list of arguments to n88solver is given in the Command Reference chapter.
4.2. Convergence
n88solver_slt is a pre-conditioned conjugate gradient solver which improves the solution through an iterative process. Therefore it is necessary to define a convergence criterion that defines when the solution is good enough, and the iterating can stop.
n88solver_slt provides the options to select from among different convergence measures. See convergence_measure.
The traditional convergence measure is the maximum change over all degrees of freedom. We call this method maximum du. Mathmatically, for the ith iteration it is defined as
where xi,j is the displacement of the jth degree of freedom at the ith iteration. The maximum is taken over all degrees of freedom.
The difficulty with this convergence measure is that it is not clear what numerical value of tolerance is optimal, as it is not obvious how it relates to quantities that a user would be directly interesting in. Although the convergence measure is unitless, there is in fact no consistent relationship between ei and the relative precision of quantities such as displacement and force. Therefore the tolerance must be chosen conservatively based on experience.
In version 8, we introduced a new convergence measure, which we call a convergence set. Essentially, this is a parameter, c, equivalent directly to a quantity of interest to the user. This parameter depends on the model. For example for a compression test with fixed strain or displacement, it would be equivalent to the reaction force on the top surface (more precisely the top boundary condition). On the other hand, if you define a compression test with a given force, in that case an appropriate parameter c would be the average displacement of the top surface. The solver continues iterations until the relative change in c from iteration to iteration falls below a specified threshold:
The choice of tolerance is now straight-forward: if you want to obtain a certain relative precision in your calculated reaction force for example, let us say one part in 104, then you allow a bit of a safety margin and chose for example a tolerance of 10-5.
Clearly the difficulty is now in defining the quantity c. Fortunately,
the standard faim model generator tools, including n88modelgenerator
and vtkbone will define a suitable one for you. For the standard
tests, it is the complement of the most important moving boundary condition,
or most important applied force, as appropriate. By the complement, we mean
that c is calculated as a force in the case of a boundary condition; conversely it is calculated as an average displacement in the case of an applied
force. The definition of c therefore consists of defining a convergence
set, which is some collection of degrees of freedom, together with some specification
of what is to be calculated over this collection of degrees of freedom.
It is exactly analogus to a constraint, which is internally how
boundary conditions and applied forces are stored in n88model files;
a convergence set is stored in a similar manner in an n88model file.
See n88model File Format. Clearly, in the case that
no convergence set is defined in the n88model file, the convergence set
method for determining convergence cannot be used. In this case, the solver
will fall back to the traditional maximum du method.
Regardless of the convergence measure chosen, the convergence measure does not decay smoothly, but can be jumpy or noisy. Therefore, a convergence window is introduced, so that iterations are not terminated prematurely by a randomly low convergence measure value. To be considered converged, the convergence measure ei must remain below the threshold for at least the specified number of consecutive iterations. For the maximum du method, we have found by experience that a convergence window of 3 is typically sufficient. For the convergence set method, because it looks at only a part of the whole model, we have found that the convergence window must be increased as the number of degrees of freedom increases. Based on empirical analysis of many models, we suggest the following formula for the convergence window
where n is the number of nodes in the model. This formula is in fact what the solver will use if you don’t explicitly chose another value with the parameter convergence_window.
In addition to the convergence criterion described above, a maximum number of iterations can be set. This is useful for stopping the iterating if the thresholds have been set too low (i.e. too strictly). Sometimes we may want to stop and perform a more sophisticated analysis of the quality of the solution before deciding if we want to proceed with further iterations.
Note that no matter how the solver terminated, we can re-launch it, possibly
with different convergence criteria. By default, the solver will use an
existing solution as the starting point and continue to refine it from
where it left off. Note however, that not all the numerical parameters of
the conjugate gradient method are stored in the n88model file. Therefore, stopping
and re-starting the solver does not result in precisely the same progression
of iterations as compared with simply letting the solver run uninterupted. Some
additional iterations are required to reconstruct the conjugate gradient
information.
If you want to make a close investigation of the convergence of your model as the solver iterates, you can make use of the iterations_file option to output all iteration data to a file. It can be informative to plot these data on a log-log graph (convergence measure ei versus iteration number i).
4.3. Evaluating solution quality
For a linear problem, the solver is solving a system equivalent to
where x are the displacements, f are the forces (including all the internal forces on each node), and K is a global stiffness matrix. The solver never actually constructs K; the memory requirements would be prohibitive, as K is a matrix of size N2, where N is the number of degrees of freedom. The residuals are defined as
For the exact solution, the residual vector is identically zero. As we are obtaining a numerical solution rather than an exact solution, we cannot in practice obtain exactly zero-valued residuals. The remaining value of the residuals is a good measure of the accuracy of the solution, with smaller residuals indicating a closer match to the unobtainable perfect solution.
To answer the question, “What is a good value for the residuals?”, observe that the residuals have units of force. We therefore need to compare with a characteristic force in the system.
Numerics88 provides a tool, n88evaluate, to evaluate a solution. It is run like this
n88evaluate myfile.n88model
The output related to the residuals looks like this
Analysis of forces (residuals):
max err : 3.00E-07
rms err : 3.15E-08
max err/max force : 3.51E-06
rms err/max force : 3.68E-07
The second two numbers are the maximum and RMS residuals, scaled to the maximum nodal force in the solution. These values are a measure of the relative error. Note that this error is only the mathematical error of the solution to the stated system of equations. There are naturally other sources of error, such as that due to the measurement and discretisation of the physical object, and the error in determining the material properties of the object. When the solver is working normally, these other sources of error will be much larger than the remaining mathematical error in the solution obtained by the solver.
n88evaluate also performs a check that the boundary conditions are
indeed satisfied:
Analysis of solution displacements at boundary conditions:
max err : 0.00E+00
rms err : 0.00E+00
This is a trivial check: anything other than zero or very small values indicates a problem with solver.
5. Solving Nonlinear Problems
5.1. Obtaining solutions to nonlinear problems with n88solver_spt
If you have defined plasticity for any materials used in your model, then you must
use the solver n88solver_spt, which is a solver suitable for small-strain elastoplastic models. This solver is invoked exactly as is n88solver_slt. It
recognizes a couple of additional options related to the plastic convergence. To solve an elastoplastic
model, the solver first obtains a linear elastic solution, and then performs a plastic
iteration to update the plastic strain. This is repeated until the plastic convergence
criterion is met. Thus linear solutions, consisting of many linear iterations, alternate
with single plastic iteration steps.
|
|
It is perfectly possible to run |
5.2. Convergence
For elastoplastic problems, the default convergence measure remains the traditional
dumax method, instead of the new convergence set method. See Convergence measure.
The reason for this is that, not infrequently the addition of plasticity has only a
small effect on quantities like reaction force. In these cases, observing a quantity
such as the total reaction force to determine convergence does not work well
for the plastic iterations. Furthermore, when solving an elastoplastic problem,
we are more likely to be interested in quantities pertaining to the entire volume,
such as the number and location of yielded elements, rather than only quantities that are
calculated over just a boundary condition, such as reaction force. Recall that the
dumax convergence measure is calculated over all degrees of freedom, while
the convergence set convergence measure is typically calculated over a chosen
boundary condition.
|
|
As was the case for linear files, you can generate a file with all the iteration data using the option iterations_file. For elastoplastic solutions, this file can be quite large. Here is a command to extract just the last linear iteration of every plastic iteration step, which often contains all the information we are looking for (i.e. the full plastic evolution, as well as the linear tolerance for each plastic iteration, and the number of linear iterations required at each plastic step). awk '$2!=previous {print line; previous=$2}
$2==previous {line = $0; previous=$2}' iterations.txt
This command can be run in Linux and macOS, as well as in a Bash shell in Windows 10. In
case you don’t have lines = open("iterations.txt").readlines()
output = [p for (l,p) in zip(lines,[lines[0]] + lines[:-1]) if l.split()[1] != p.split()[1]]
for o in output: print o,
|
5.3. Obtaining accurate nonlinear solutions by progressively applying loads
In contrast to a linear elastic model, there is in general no single unique solution for a given end-state of a system with elastoplastic characteristics. As discussed in the section plasticity in the chapter Preparing Finite Element Models with n88modelgenerator, elastoplastic models exhibit irreversibility and hysteresis, and thus have a path dependence. In other words, a dependence not only on the final state, but on the history in obtaining the final state. For a real object, the history is the time-dependence of the state, presumably starting from some initial neutral state. Within the solver, it is not necessary (or possible) to account for a continuous time dependence of the state: nevertheless even if we solve for a single end state of an elastoplastic model, the solver necessarily traces a path in a mathematical space from some starting point to the final solution. Just as for the real physical situation, this path in mathematical space can affect the final solution. Therefore, the most strictly correct approach to solving nonlinear elastoplastic problems is to incrementally apply loads (or strains), starting with a solution at or near the elastic limit (i.e. near the onset of nonlinear behaviour), and obtaining a complete solution at each load increment, until the final state is obtained. This is obviously more complicated than a single all-at-once solution, and also more time-consuming. The question is, does this make any practical difference? Frequently, for loads applied monotonically in a single direction, the answer is no. Conversly, if your physical situation involves increasing and decreasing a load, or changing the direction of an applied load, then it is important to model this load history. A tutorial demonstrating the incremental application of a load to an elastoplastic problem is A cantilevered beam with elastoplastic material properties .
5.4. Evaluating nonlinear solution quality
Evaluating the correctness of an elastoplastic solution is more subtle than evaluating the correctness of a linear elastic model, for the simple reason that, as mentioned in the previous section, there is no single unique solution to an elastoplastic problem.
There are nevertheless some measures we can use. Internal forces must still balance, and we can examine the residuals, as in Evaluating solution quality in the section on linear models.
When examining the yield strain, there must be no unyielded elements for which a positive yield function is calculated. Here is the check of that in n88evaluate:
Analysis of yield function F:
Unyielded elements with F>0:
count : 0
max F : -
rms F : -
max F/max stress : -
rms F/max stress : -
Actually in rare cases, a small number of unyielded elements might have very small positive values of yield function, but in this case, the values should be very small indeed.
Secondly, one might expect all the yielded elements in the solution (i.e. those elements with a nonzero plastic strain) to lie on the yield surface (F=0). In fact, this is not necessarily the case. Even in an elastoplastic model carefully solved with incremental applied test strain, it may happen that some elements reach the yield stress (i.e. the yield surface) for some value of applied test strain, but then actually experience a substantially reduced stress at a higher applied test strain, due to the mechanical failure or yield of some other part of the model. Thus it is perfectly possible to have an end-state solution in which some elements are observed to have non-zero plastic strains but are in a stress state much less than the yield stress (i.e. well inside the yield surface). More common though is for yield elements to have a very small remnant positive yield function, which is somewhat analogous to the residual in the linear case.
Values related to the yield function calculated for all yielded elements are reported by n88evaluate, as shown in this example:
Analysis of yield function F:
Yielded elements:
count : 2058
min F : -1.85E+01
max F : 1.08E-04
rms F : 7.77E+00
min F/max stress : -2.12E-01
max F/max stress : 1.23E-06
rms F/max stress : 8.88E-02
In light of the above discussion, the important value is max F/max stress: it can
be used as a measure of the relative error of the plastic component
of the solution.
6. Post-Processing and Analysis
6.1. Calculating additional solution fields with n88derivedfields
The fundamental solution from n88solver are the displacements on each node. However,
this is often not the only value of interest. Subsequently running
n88derivedfields on the n88model file will generate additional
fields and add them to the active solution in the file.
|
|
To check which solution fields are present in a n88modelinfo --solutions your_model.n88model |
The following are the additional fields that will be added to the n88model
file by n88derivedfields.
The reaction force at each node, in the 3 coordinate directions (fx,fy,fz). For a linear problem the reaction force is given by
This is of course the same equation that the solver has solved, except that now we use it with the solution values for x (the displacements) to determine forces. If the solution is accurate, then the forces will be nearly all zero, except on degrees of freedom where a boundary condition (displacement or applied force) applies. Those therefore are the interesting values.
The strain at each element, given by εxx, εyy, εzz, γyz, γzx, γxy, where εii is the engineering normal strain along the axis direction i, and the γij are the engineering shear strains.
Note that the field Strain is always the total strain, so that for
elasto-plastic models, the elastic strain can be obtained by
subtracting PlasticStrain from Strain.
The plastic strain at each element. The plastic strain is the
irreversible strain that arises from further deformation once the
elastic limits as defined by the yield surface as been reached.
PlasticStrain has the same 6 components as Strain.
The stress at each element, given by σxx, σyy, σzz, σyz, σzx, σxy .
Note that the stress can be obtained directly from the strain (and vice versa) using the material properties. See Elastic material properties.
The von Mises stress is a scalar value that is frequently used as a yield criterion. It is also used as a heuristic measure of the “magnitude” of the stress at a point, for example for the purpose of coloring a rendering according to stress concentration. It is defined on each element by
It can also be expressed more concisely as a norm of the devatoric stresses. For details refer to any Mechanics of Solids textbook.
The strain energy density is given by
This expression continues to be valid even for nonlinear elastoplastic models, provided that the strain values are limited to the elastic strain component.
In a finite element context, the strain energy density is a scalar value defined on each element.
6.2. Exporting solution fields from the model file
If n88postfaim, which is described in the next section,
provides the values which are of interest to you, you will not need the
numerical data of the solution fields. In other cases, where you want do some custom post-processing on the
solution, it will be necessary to obtain the solution fields as array data.
There are several options for obtaining the field data from an n88model
file:
-
Use n88extractfields to export fields to a text file. This is convenient because text files are easy to understand and easy to import. The trade off is that text files are inefficient in terms of disk space required, and relatively slow to write and read.
-
Use the
vtkboneobject vtkboneN88ModelReader . This requires writing some code in C++ or Python. -
Import the data into third party software that can read NetCDF4 or HDF5.
6.3. Obtaining standard post-processing values with n88postfaim
n88postfaim is a tool performs a number of standard analyses
on a solved n88model file. It produces a text file output
reporting summarized results in a table format.
6.3.1. Running n88postfaim
n88postfaim requires that n88derivedfields has been
run on the solved n88model file because it makes use of the derived fields.
If any field is required for a particular table, but is not present in
the n88model file, n88postfaim will simply silently skip that table.
In the usual case, running n88postfaim is as simple as,
n88postfaim -o analysis.txt radius_slice82_bending.n88model
This will generate an output file analysis.txt. The output is a report of
values that are commonly of interest in finite element calculations.
The sections below will discuss a few important options that affect
the output of n88postfaim. For a complete list of arguments supported by
n88postfaim, see the Command Reference chapter.
|
|
The model n88modelgenerator --test=bending radius_slice82.aim This data file is provided for the radius compression tutorial, but here we apply a bending test so that angular analysis quantities such as torques are defined. This model also has been segmented to have more than one material ID. In particular, ID 127 is used to identify cortical bone and ID 100 is used to identify cancellous bone. This applies to all tables except Plastic Strain,
for which the flag |
Specifying post-processing node and element sets
Some of the quantities that n88postfaim reports are calculated with
respect to defined node and/or element sets. For example, for a
compression test, the forces on the top and bottom surfaces are of interest.
If we define node and element sets corresponding to these surfaces,
then n88postfaim will, amongst other things, calculate these forces for us.
Post-processing node and element sets must be defined during
the model generation stage.
If you used n88modelgenerator, some relevant node and
element sets have automatically been defined. For custom models generated
with vtkbone see
Creating node and element sets.
The available sets in an n88model file can be discovered with
n88modelinfo. For example, the command
n88modelinfo --sets --element_sets radius_slice82_bending.n88model
gives the following output:
NodeSets: ---------------------------------------------------------------------- Name : face_z0 Part : Part1 NumberOfNodes : 40032 Name : face_z1 Part : Part1 NumberOfNodes : 25991 Name : face_x0 Part : Part1 NumberOfNodes : 15 Name : face_x1 Part : Part1 NumberOfNodes : 14 Name : face_y0 Part : Part1 NumberOfNodes : 27 Name : face_y1 Part : Part1 NumberOfNodes : 17 ---------------------------------------------------------------------- ElementSets: ---------------------------------------------------------------------- Name : face_z0 Part : Part1 NumberOfElements : 28999 Name : face_z1 Part : Part1 NumberOfElements : 21210 Name : face_x0 Part : Part1 NumberOfElements : 8 Name : face_x1 Part : Part1 NumberOfElements : 6 Name : face_y0 Part : Part1 NumberOfElements : 12 Name : face_y1 Part : Part1 NumberOfElements : 8 ----------------------------------------------------------------------
Given that the sets of interest have been generated and are present in
the n88model file, we must tell n88postfaim
which to actually use. Much of the time this is also done at the
model generation stage. For models generated with vtkbone, see
Setting post-processing parameters.
n88modelgenerator also writes a list of
sets to use into the n88model file, but note that this list often
does not encompass all of the available sets.
For example, for any type of compression test, n88modelgenerator
will only list the top and bottom surface sets to be used for post-processing,
although it generates node and element sets for all faces. In a confined test the forces on the side
faces are sometimes of interest, so this may be a case where the
list of post-processing sets as generated by
n88modelgenerator is insufficient. n88postfaim has
command line options that allow us to override the list of post-processing sets from the n88model file. Here an example:
n88postfaim --node_sets face_y0,face_y1 --element_sets face_y0,face_y1 -o analysis.txt radius_slice82_bending.n88model
Note that for each node set, n88postfaim requires the corresponding element
set. For example,
for a set consisting of all the nodes on a surface, we also require the
set of all
elements on the surface. n88modelgenerator (and vtkbone objects
which generate sets automatically)
will generate sets such that the corresponding node and element sets have the
same names. If this is the case, that we have matching node and element sets,
then a simpler but equivalent version of the above example command is
n88postfaim --sets face_y0,face_y1 -o analysis.txt radius_slice82_bending.n88model
Specifying a rotation center
Certain quantities, such as rotations and torques, are calculated relative to a reference point, or center. This reference point can be specified in a number of ways:
-
For bending and torsion tests, n88modelgenerator will write a default rotation center into the
n88modelfile, which will be located at the center of mass of the model. -
n88modelgenerator supports an argument central_axis that allows the reference point to be specified, as numerical coordinates or as the center of mass or the center of bounds. The reference value will be written to the
n88modelfile. If specified, it overrides the above default. -
n88postfaimsupports an argument rotation_center that can be used to specify the reference point. If specified, it overrides any value in then88modelfile.
If the rotation point is not specified in one of these ways, then the corresponding analysis values and tables will not be calculated or reported. This simplifies the analysis output for models for which these values are typically not of interest (e.g. an axial compression test).
6.3.2. Description of output tables
Below are listed the tables provided in the output of n88postfaim.
Note that not all values or tables are generated for every model. Angular values are generated only if a rotation center is defined (see the above section), while a break-down of values per material is only performed in the case that more than one material is defined.
|
|
n88postfaim knows nothing of the Test Frame coordinate system
(see Test Orientation). All coordinate
directions in the analysis file are in the original Data Frame coordinate
system. An exception is that the names of the sets, as assigned
by n88modelgenerator and listed in Node and element sets generated by vtkboneApplyTestBase,
are obtained from their orientation in the Test Frame.
|
|
|
The table numbering is not fixed. Tables are simply numbered sequentially at the time they are generated. You cannot rely on a certain table number consistently identifying a given table. |
Model Input
This table lists general parameters of the model input.
Table 1: Model Input ---------------------------------------------------------------------------- Filename: radius_slice82_bending.n88model Element dim X: 0.082 Element dim Y: 0.082 Element dim Z: 0.082 Number of elements: 2667590 Number of nodes: 3816642 Number of nodes per element: 8 Dimension of problem: 3
Materials
The material definitions as assigned to each material ID are listed. In addition, a very brief summary of the material definition is provided, in particular the material type is shown, and a rough indication of the stiffness is given by the parameter Eii_max. For an isotropic material, Eii_max is the Youngs modulus E, while for an orthotropic material it is the maximum of Exx, Eyy, and Ezz . In addition, the total number of elements in the model having each material ID are shown, giving a measure of the distribution of the materials.
Table 2: Materials ---------------------------------------------------------------------------- Number of materials: 2 ---------------------------------------------------------------------------- m ID Name Type E_ii_max Elements 1 100 NewMaterial1 LinearIsotropic 6829.0 1351375 2 127 NewMaterial1 LinearIsotropic 6829.0 1316215
Note that in this example, it happens that although we have two material IDs (defined during segmentation), they are both assigned to the same material definition.
The output will be somewhat different for material arrays, since material arrays correspond to a range of material IDs. Here is an example:
Table 2: Materials ---------------------------------------------------------------------------- Number of materials: 1 ---------------------------------------------------------------------------- m ID Name Type E_ii_max Elements 1 1..127 NewMaterial1_homminga LinearIsotropic - 7087
Also, for any of the tables described below for which sub-tables for each material ID are generated, it is to be noted that all material IDs corresponding to a material array are grouped into a single subtable. This prevents the amount of output from becoming excessive.
If you require more details about the materials defined, we recommend that you use the n88modelinfo command. For example
n88modelinfo --materials radius_slice82_bending.n88model
Post-processing sets
The sets used by n88postfaim are reported. See
Specifying post-processing node and element sets .
Table 3: Post-processing Sets
----------------------------------------------------------------------------
Number of sets: 2
----------------------------------------------------------------------------
n Node set name Nodes Element set name Elements
1 face_z1 25991 face_z1 21210
2 face_z0 40032 face_z0 28999
Strain
Statistics of the six strain components for each element,
namely the three engineering normal strains
εxx, εyy, εzz
and the three engineering shear strains
γyz, γzx, γxy
For models with elastoplastic material definitions, the strain given here is the total strain (i.e. the sum of the elastic and plastic strains).
The strains are summarized in terms of statistical quantities, namely average, standard deviation, minimum and maximum, and skewness and kurtosis. The median strain, 5th, 25th, 75th and 95th percentile strains are reported. Finally, the fraction of strains that are below zero (i.e. compressive strain) is reported in addition to the median and average strain of the negative (compressive) and positive (tensile) strain.
The summary of strains is provided for all elements in the model as well as being summarized for each specific material ID in the case of more than one defined material. In this example model, this provides a means of considering differences in the summary of strains in the cortex (e.g. material ID 127) separately from trabecular (e.g. material ID 100) bone.
Strain is dimensionless.
Table 4: Strain
----------------------------------------------------------------------------
m: ALL
Material ID: ALL
............................................................................
epsilon_xx epsilon_yy epsilon_zz gamma_yz gamma_zx gamma_xy
average -3.190E-04 -1.595E-04 5.405E-04 -7.457E-06 -2.048E-03 -3.663E-05
std_dev 2.099E-03 1.544E-03 6.843E-03 2.937E-03 4.153E-03 1.403E-03
minimum -2.150E-02 -1.771E-02 -6.982E-02 -5.306E-02 -7.585E-02 -3.298E-02
maximum 1.734E-02 2.012E-02 7.162E-02 4.388E-02 4.232E-02 2.821E-02
skewness -7.522E-01 -1.510E-01 4.932E-01 -8.113E-01 -9.770E-01 6.881E-02
kurtosis 1.184E+00 2.076E+00 3.916E-01 7.286E+00 3.599E+00 7.669E+00
median -3.340E-05 -8.509E-06 -1.603E-05 1.328E-04 -9.438E-04 -3.450E-05
perc05 -4.750E-03 -2.959E-03 -9.953E-03 -5.143E-03 -9.573E-03 -2.163E-03
perc25 -1.070E-03 -8.355E-04 -3.705E-03 -9.735E-04 -4.461E-03 -6.944E-04
perc75 7.472E-04 5.336E-04 3.638E-03 1.404E-03 3.828E-04 6.016E-04
perc95 2.837E-03 2.399E-03 1.409E-02 4.025E-03 3.254E-03 2.158E-03
----------------------------------------------------------------------------
m: 1
Material ID: 100
............................................................................
epsilon_xx epsilon_yy epsilon_zz gamma_yz gamma_zx gamma_xy
average -3.326E-04 -2.304E-04 9.468E-04 -2.711E-04 8.815E-05 -1.733E-05
std_dev 1.403E-03 1.296E-03 4.307E-03 2.824E-03 2.967E-03 1.433E-03
minimum -2.057E-02 -1.771E-02 -4.567E-02 -5.306E-02 -5.665E-02 -3.298E-02
maximum 1.734E-02 2.012E-02 6.647E-02 4.388E-02 4.232E-02 2.821E-02
skewness -9.487E-01 -5.547E-01 8.212E-01 -8.143E-01 -8.987E-01 -5.569E-02
kurtosis 5.294E+00 4.647E+00 4.572E+00 1.121E+01 9.849E+00 1.051E+01
median -9.529E-05 -5.413E-05 1.652E-04 -1.758E-05 7.115E-05 -7.972E-06
----------------------------------------------------------------------------
m: 2
Material ID: 127
............................................................................
epsilon_xx epsilon_yy epsilon_zz gamma_yz gamma_zx gamma_xy
average -3.049E-04 -8.671E-05 1.232E-04 2.632E-04 -4.240E-03 -5.645E-05
std_dev 2.629E-03 1.760E-03 8.690E-03 3.025E-03 4.054E-03 1.372E-03
minimum -2.150E-02 -1.667E-02 -6.982E-02 -3.880E-02 -7.585E-02 -1.501E-02
maximum 1.322E-02 1.588E-02 7.162E-02 3.375E-02 2.053E-02 2.617E-02
skewness -6.398E-01 -3.604E-02 4.942E-01 -8.592E-01 -1.007E+00 2.105E-01
kurtosis -2.316E-01 7.413E-01 -7.675E-01 4.422E+00 3.701E+00 4.171E+00
median 1.376E-04 9.347E-05 -2.057E-03 6.242E-04 -4.044E-03 -9.920E-05
Skewness is a measure of the asymmetry of the distribution of element stresses. Kurtosis is a measure of the “peakedness” of the distribution of element stresses.
Plastic Strain
For models with elastoplastic material definitions, a table of plastic strain statistics is produced. To obtain the elastic strain, subtract the plastic strain from the total strain, given in the previous table.
The presentation of the plastic strain the same format as for the total strain.
Plastic strain is dimensionless.
============================================================================
Table 5: Plastic Strain
----------------------------------------------------------------------------
m: ALL
Material ID: ALL
............................................................................
epsilon_xx epsilon_yy epsilon_zz gamma_yz gamma_zx gamma_xy
average -3.774E-04 -1.827E-04 5.602E-04 -2.491E-05 -1.051E-03 -4.255E-05
std_dev 2.441E-03 1.858E-03 4.103E-03 2.424E-03 3.285E-03 9.990E-04
minimum -6.403E-02 -6.146E-02 -9.844E-02 -1.862E-01 -1.647E-01 -1.062E-01
maximum 4.919E-02 4.925E-02 1.223E-01 1.418E-01 1.750E-01 7.206E-02
skewness -1.856E+00 -7.680E-01 1.454E+00 -3.772E+00 -3.946E+00 2.007E+00
kurtosis 1.172E+01 1.926E+01 1.147E+01 2.736E+02 8.944E+01 2.992E+02
median 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00
perc05 -5.234E-03 -3.476E-03 -5.073E-03 -2.307E-03 -6.641E-03 -1.150E-03
perc25 0.000E+00 0.000E+00 0.000E+00 0.000E+00 -9.717E-04 -5.828E-06
perc75 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00
perc95 2.724E-03 2.380E-03 8.666E-03 2.226E-03 5.648E-04 9.484E-04
----------------------------------------------------------------------------
m: 1
Material ID: 100
............................................................................
epsilon_xx epsilon_yy epsilon_zz gamma_yz gamma_zx gamma_xy
average -2.516E-04 -2.011E-04 4.528E-04 -1.325E-04 -3.686E-05 2.363E-06
std_dev 1.569E-03 1.441E-03 2.876E-03 2.513E-03 2.424E-03 9.711E-04
minimum -6.084E-02 -6.146E-02 -9.844E-02 -1.862E-01 -1.647E-01 -1.062E-01
maximum 4.919E-02 4.925E-02 1.223E-01 1.418E-01 1.750E-01 6.961E-02
skewness -4.158E+00 -3.443E+00 3.959E+00 -5.739E+00 -3.362E+00 5.373E-02
kurtosis 5.475E+01 5.797E+01 5.475E+01 4.191E+02 3.503E+02 4.686E+02
median 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00 0.000E+00
----------------------------------------------------------------------------
m: 2
Material ID: 127
............................................................................
epsilon_xx epsilon_yy epsilon_zz gamma_yz gamma_zx gamma_xy
average -5.066E-04 -1.638E-04 6.704E-04 8.559E-05 -2.093E-03 -8.867E-05
std_dev 3.085E-03 2.205E-03 5.060E-03 2.324E-03 3.700E-03 1.025E-03
minimum -6.403E-02 -4.663E-02 -7.185E-02 -1.076E-01 -1.294E-01 -2.535E-02
maximum 3.604E-02 4.230E-02 1.107E-01 8.670E-02 3.620E-02 7.206E-02
skewness -1.209E+00 4.159E-02 7.811E-01 -1.199E+00 -4.140E+00 3.735E+00
kurtosis 4.603E+00 8.276E+00 3.481E+00 6.679E+01 4.224E+01 1.604E+02
median 0.000E+00 0.000E+00 0.000E+00 0.000E+00 -5.584E-04 0.000E+00
============================================================================
Stress
Statistics of the six stress components for each element, including the normal stresses
(σxx, σyy, σzz) and shear
stresses (σyz, σzx, σxy).
The presentation of the stress follows the same format as described for the Strain table.
Units depend on inputs, but typically displacements are expressed in millimeters (mm), forces in newtons (N), and stresses in MPa. See Note about units.
Table 6: Stress
----------------------------------------------------------------------------
m: ALL
Material ID: ALL
............................................................................
sigma_xx sigma_yy sigma_zz sigma_yz sigma_zx sigma_xy
average -8.027E-01 -5.936E-01 3.083E+00 -1.959E-02 -5.378E+00 -9.621E-02
std_dev 1.315E+01 1.070E+01 5.073E+01 7.714E+00 1.091E+01 3.686E+00
minimum -2.380E+02 -2.004E+02 -5.796E+02 -1.394E+02 -1.992E+02 -8.662E+01
maximum 1.682E+02 1.632E+02 5.517E+02 1.153E+02 1.111E+02 7.410E+01
skewness -5.570E-01 4.960E-01 4.539E-01 -8.113E-01 -9.770E-01 6.881E-02
kurtosis 5.054E+00 4.068E+00 4.404E-01 7.286E+00 3.599E+00 7.669E+00
median -4.492E-01 -3.217E-01 -2.718E-01 3.489E-01 -2.479E+00 -9.062E-02
perc05 -2.244E+01 -1.716E+01 -7.487E+01 -1.351E+01 -2.514E+01 -5.681E+00
perc25 -7.064E+00 -5.724E+00 -2.868E+01 -2.557E+00 -1.172E+01 -1.824E+00
perc75 5.727E+00 2.874E+00 2.650E+01 3.687E+00 1.005E+00 1.580E+00
perc95 1.979E+01 1.944E+01 1.020E+02 1.057E+01 8.546E+00 5.668E+00
----------------------------------------------------------------------------
m: 1
Material ID: 100
............................................................................
sigma_xx sigma_yy sigma_zz sigma_yz sigma_zx sigma_xy
average 6.726E-01 3.019E-01 6.486E+00 -7.120E-01 2.315E-01 -4.551E-02
std_dev 1.009E+01 7.009E+00 3.126E+01 7.418E+00 7.793E+00 3.764E+00
minimum -1.424E+02 -1.625E+02 -3.346E+02 -1.394E+02 -1.488E+02 -8.662E+01
maximum 1.682E+02 1.632E+02 5.062E+02 1.153E+02 1.111E+02 7.410E+01
skewness 3.128E-03 4.413E-01 7.910E-01 -8.143E-01 -8.987E-01 -5.569E-02
kurtosis 8.270E+00 1.406E+01 4.799E+00 1.121E+01 9.849E+00 1.051E+01
median 8.653E-02 -4.944E-03 8.636E-01 -4.619E-02 1.869E-01 -2.094E-02
----------------------------------------------------------------------------
m: 2
Material ID: 127
............................................................................
sigma_xx sigma_yy sigma_zz sigma_yz sigma_zx sigma_xy
average -2.317E+00 -1.513E+00 -4.100E-01 6.914E-01 -1.114E+01 -1.483E-01
std_dev 1.554E+01 1.341E+01 6.472E+01 7.944E+00 1.065E+01 3.604E+00
minimum -2.380E+02 -2.004E+02 -5.796E+02 -1.019E+02 -1.992E+02 -3.943E+01
maximum 1.506E+02 1.427E+02 5.517E+02 8.865E+01 5.392E+01 6.873E+01
skewness -5.163E-01 5.951E-01 4.757E-01 -8.592E-01 -1.007E+00 2.105E-01
kurtosis 3.035E+00 1.604E+00 -7.415E-01 4.422E+00 3.701E+00 4.171E+00
median -3.882E+00 -2.612E+00 -1.698E+01 1.640E+00 -1.062E+01 -2.606E-01
Strain Energy Density
Statistics on the strain energy density are reported. See StrainEnergyDensity in n88derivedfields for a definition of the strain energy density.
For models with elastoplastic material definitions, the strain energy density is the elastic strain energy density. (Plastic strain energy density is not well defined: the work done producing a given a plastic strain is mostly converted into heat energy and cannot be retreived again as mechanical work.)
The presentation of the strain energy density follows the same format as described for the Strain table.
Table 7: Strain Energy Density ---------------------------------------------------------------------------- m: ALL Material ID: ALL ............................................................................ average 2.091E-01 std_dev 3.039E-01 minimum 5.704E-15 maximum 2.186E+01 skewness 4.357E+00 kurtosis 9.588E+01 median 8.209E-02 perc05 4.649E-04 perc25 1.149E-02 perc75 2.918E-01 perc95 8.012E-01 ---------------------------------------------------------------------------- m: 1 Material ID: 100 ............................................................................ average 9.484E-02 std_dev 2.108E-01 minimum 5.704E-15 maximum 1.662E+01 skewness 7.458E+00 kurtosis 1.533E+02 median 1.993E-02 ---------------------------------------------------------------------------- m: 2 Material ID: 127 ............................................................................ average 3.264E-01 std_dev 3.382E-01 minimum 1.353E-12 maximum 2.186E+01 skewness 3.914E+00 kurtosis 9.946E+01 median 2.203E-01
Von Mises Stress
Statistics on the von Mises stress are reported. See VonMisesStress in n88derivedfields for a definition of the von Mises stress.
The presentation of the von Mises stress follows the same format as for the Strain table.
Table 8: Von Mises Stress ---------------------------------------------------------------------------- m: ALL Material ID: ALL ............................................................................ average 3.920E+01 std_dev 3.147E+01 minimum 9.139E-06 maximum 4.915E+02 skewness 8.934E-01 kurtosis 5.365E-01 median 3.204E+01 perc05 2.624E+00 perc25 1.251E+01 perc75 5.944E+01 perc95 9.817E+01 ---------------------------------------------------------------------------- m: 1 Material ID: 100 ............................................................................ average 2.455E+01 std_dev 2.461E+01 minimum 9.139E-06 maximum 4.237E+02 skewness 1.832E+00 kurtosis 4.876E+00 median 1.643E+01 ---------------------------------------------------------------------------- m: 2 Material ID: 127 ............................................................................ average 5.423E+01 std_dev 3.065E+01 minimum 1.460E-04 maximum 4.915E+02 skewness 4.575E-01 kurtosis 1.077E-01 median 5.081E+01
Nodal Displacements
The three components of displacements (ux,
uy, uz) are reported. A sub-table is
generated for each post-processing node set. Statistics of
the displacements are reported over all the nodes of each
set.
Units are self-consistent, but are typically millimeters (mm). See A note about units.
Table 9: Nodal Displacements
----------------------------------------------------------------------------
Node set: 1
Name: face_z1
............................................................................
ux uy uz
average 0.000E+00 0.000E+00 8.493E-03
std_dev 0.000E+00 0.000E+00 3.727E-02
minimum 0.000E+00 0.000E+00 -6.689E-02
maximum 0.000E+00 0.000E+00 7.695E-02
median 0.000E+00 0.000E+00 7.534E-03
----------------------------------------------------------------------------
Node set: 2
Name: face_z0
............................................................................
ux uy uz
average 0.000E+00 0.000E+00 8.176E-03
std_dev 0.000E+00 0.000E+00 5.033E-02
minimum 0.000E+00 0.000E+00 -8.768E-02
maximum 0.000E+00 0.000E+00 1.392E-01
median 0.000E+00 0.000E+00 1.250E-02
Nodal Forces
The three components of force (Fx, Fy, Fz) are reported. A sub-table is
generated for each post-processing element set. The forces
are provided giving statistical values over all elements in the set.
Units depend on inputs, but are typically Newtons (N). See A note about units.
Table 10: Nodal Forces
----------------------------------------------------------------------------
Node set: 1
Name: face_z1
............................................................................
Fx Fy Fz
total -8.767E+02 -3.222E+00 5.025E+02
average -3.373E-02 -1.240E-04 1.933E-02
std_dev 7.261E-02 3.936E-02 3.336E-01
minimum -8.420E-01 -3.484E-01 -2.614E+00
maximum 4.068E-01 6.302E-01 1.399E+00
median -2.464E-02 -4.476E-04 4.233E-03
----------------------------------------------------------------------------
Node set: 2
Name: face_z0
............................................................................
Fx Fy Fz
total 8.773E+02 3.162E+00 -5.032E+02
average 2.191E-02 7.898E-05 -1.257E-02
std_dev 7.203E-02 5.302E-02 2.423E-01
minimum -3.655E-01 -3.909E-01 -1.399E+00
maximum 4.889E-01 3.679E-01 1.196E+00
median 8.519E-04 -2.016E-03 3.913E-03
Nodal Twist
Similar to nodal displacements, statistics on the angular displacements for each node set are provided.
The angular displacements are defined as the projected angles between the
vector to the initial location of the node and the vector to the displaced
location of the node. The vectors are projected onto a plane perpendicular to
the specified axis. This is shown in Figure 14, which defines
ROTx. p is the initial position of the node, and p' is the displaced
position of the node, as calculated by FE. These two vectors are projected
onto the y-z plane, and the angle between them in this plane is defined as
ROTx. ROTy and ROTz are similarly defined. Angular displacements are
relative to the center of rotation; this is shown as p0 in
Figure 14. See specifying a rotation center.
|
|
ROTx, ROTy, ROTz do not form a set of Euler angles.
|
Nodes that are within an exclusion radius (default value 10-6) of the rotation center are excluded from the calculation, as the angular displacement of a node at the rotation center (initial or final position) is not defined.
Units are radians (rad).
Table 11: Nodal Twist
----------------------------------------------------------------------------
Twist measured relative to: 66.049 54.985 4.510
Exclusion radius: 1.0E-06
----------------------------------------------------------------------------
Node set: 1
Name: face_z1
............................................................................
ROTx ROTy ROTz
n 25991 25991 25991
average 5.978E-04 -3.252E-03 0.000E+00
std_dev 3.424E-03 2.180E-03 0.000E+00
minimum -8.422E-03 -6.893E-03 0.000E+00
maximum 7.567E-03 -6.411E-07 0.000E+00
median 6.324E-04 -3.274E-03 0.000E+00
----------------------------------------------------------------------------
Node set: 2
Name: face_z0
............................................................................
ROTx ROTy ROTz
n 40032 40032 40032
average -7.531E-04 4.147E-03 0.000E+00
std_dev 4.239E-03 2.363E-03 0.000E+00
minimum -1.014E-02 6.411E-07 0.000E+00
maximum 9.126E-03 8.099E-03 0.000E+00
median -3.388E-04 4.688E-03 0.000E+00
Nodal Torques
Similar to nodal twist, statistics on the the nodal torques for each node set are reported.
As with the nodal twist results, torques are calculated relative to a reference point. See specifying a rotation center.
Units depend on inputs, but are typically in newton-millimeters (Nmm). See Note about units.
Table 12: Nodal Torques
----------------------------------------------------------------------------
Torque measured relative to: 66.049 54.985 4.510
----------------------------------------------------------------------------
Node set: 1
Name: face_z1
............................................................................
Tx Ty Tz
total 1.094E+04 -3.683E+04 -1.796E+03
average 4.210E-01 -1.417E+00 -6.909E-02
std_dev 2.312E+00 1.847E+00 7.455E-01
minimum -5.420E+00 -2.341E+01 -9.929E+00
maximum 3.204E+01 1.070E-01 5.532E+00
median 2.183E-02 -6.439E-01 -2.549E-03
----------------------------------------------------------------------------
Node set: 2
Name: face_z0
............................................................................
Tx Ty Tz
total -1.094E+04 3.682E+04 1.796E+03
average -2.733E-01 9.198E-01 4.486E-02
std_dev 1.487E+00 1.466E+00 5.923E-01
minimum -1.111E+01 -3.944E+00 -3.920E+00
maximum 7.102E+00 1.176E+01 5.743E+00
median -4.530E-03 3.083E-01 -2.374E-03
Load Sharing
A calculation of the fraction of the load carried by each material ID is provided, based on the nodal forces in each associated node set.
The portion of total load on the node set is reported for each material in terms of nodal forces (Fx, Fy, Fz). Nodal torques (Tx, Ty, Tz) are also reported if a center of rotation is defined. See specifying a rotation center. The total forces and torques are also reported, and it should be noted that are the same as reported in Nodal Forces and Nodal Torques
The method used to determine the loads carried by each material requires identifying the nodes belonging to each material. Since material definitions are based on elements, some nodes are shared by more than one material. In these cases, the forces and torques associated with the node are proportionally assigned to each material definition.
Table 13: Load Sharing
----------------------------------------------------------------------------
Torque measured relative to: 66.0487 54.9845 4.5100
----------------------------------------------------------------------------
Node set: 1
Name: face_z1
............................................................................
material Fx Fy Fz
100 -2.2735E+02 2.2343E+01 1.5989E+02  127 -6.4936E+02 -2.5565E+01 3.4260E+02
---------- ---------- ---------- ----------
total -8.7671E+02 -3.2224E+00 5.0249E+02
127 -6.4936E+02 -2.5565E+01 3.4260E+02
---------- ---------- ---------- ----------
total -8.7671E+02 -3.2224E+00 5.0249E+02 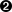 material Tx Ty Tz
100 1.3237E+03 -4.6310E+03 -5.3746E+02
127 9.6174E+03 -3.2197E+04 -1.2583E+03
---------- ---------- ---------- ----------
total 1.0941E+04 -3.6828E+04 -1.7958E+03
----------------------------------------------------------------------------
Node set: 2
Name: face_z0
............................................................................
material Fx Fy Fz
100 -8.0150E+01 1.3524E+02 -2.2235E+02
127 9.5741E+02 -1.3208E+02 -2.8086E+02
---------- ---------- ---------- ----------
total 8.7726E+02 3.1616E+00 -5.0321E+02
material Tx Ty Tz
100 -4.4656E+03 1.5580E+04 1.3600E+02
127 -6.4737E+03 2.1242E+04 1.6599E+03
---------- ---------- ---------- ----------
total -1.0939E+04 3.6823E+04 1.7959E+03
material Tx Ty Tz
100 1.3237E+03 -4.6310E+03 -5.3746E+02
127 9.6174E+03 -3.2197E+04 -1.2583E+03
---------- ---------- ---------- ----------
total 1.0941E+04 -3.6828E+04 -1.7958E+03
----------------------------------------------------------------------------
Node set: 2
Name: face_z0
............................................................................
material Fx Fy Fz
100 -8.0150E+01 1.3524E+02 -2.2235E+02
127 9.5741E+02 -1.3208E+02 -2.8086E+02
---------- ---------- ---------- ----------
total 8.7726E+02 3.1616E+00 -5.0321E+02
material Tx Ty Tz
100 -4.4656E+03 1.5580E+04 1.3600E+02
127 -6.4737E+03 2.1242E+04 1.6599E+03
---------- ---------- ---------- ----------
total -1.0939E+04 3.6823E+04 1.7959E+03
| Represents the total force attributed to material definition 127 (cortical bone in this model). | |
This result is the same as the total Fz in
Nodal Forces. |
6.4. Tabulating results from analysis files
The analysis file generated by n88postfaim is intended to be human-readable. If you run several similar models, it is common to want to tabulate certain numerical results in spreadsheet format. It is possible, but tiresome, to open the analysis file for each solved model individually and manually search for the desired numbers. To make this process more efficient, we provide the tool n88tabulate. See n88tabulate. This tool extracts certain specified values from any number of analysis files and collates them into a tabular format suitable for importing into a spreadsheet.
7. Tutorials
This chapter presents a number of tutorials to help you learn the Faim finite element tools.
A zip file containing the data files used for the tutorials, as well as the tutorial scripts, can be downloaded from http://numerics88.com/downloads/ .
The first series of tutorials introduces the standard work flow for Faim, where standard models as generated by n88modelgenerator are desired. These tutorials are:
These are intended to be followed in order, as each one builds on the previous.
Following these introductory tutorials is a series dealing with more advanced topics.
There is a tutorial that introduces models with nonlinear elasto-plastic material properties.
Then there are a series of tutorials which present the building of custom models using vtkbone. This series is intended only for those who find
n88modelgenerator insufficiently flexible for their needs. The tutorials
in this series are:
Finally, some additional examples are provided with the distribution. These are not described in the manual, but demonstrate addition concepts or functionality.
7.1. Introductory tutorial: Compressing a solid cube
We start with a very simple example, where we compress a uniform homogenous cube. This tutorial will demonstrate:
-
How to use the standard test generator
n88modelgeneratorto generate a finite element model suitable for input to the solver. -
How to solve the model.
-
How to use ParaView to visualize the model and the solution.
-
How to identify key values in the analysis file.
The data file is cube6x6x6.vti. It can be found in the data folder of
the the tutorial zip file available for download from http://numerics88.com/downloads/ .
We recommend that you copy it to a temporary working
directory for this tutorial.
You can examine this data file, which we will be using as input, with
ParaView. To do this, open ParaView
and select the menu item , and navigate to the location
of cube6x6x6.vti. You will notice that after selecting the file and
clicking OK, nothing is displayed, although the file name now appears in
the Pipeline Browser. This is typical for ParaView, and allows options
relevant to the source to be modified before the data is actually loaded.
In this case, there are no options we are concerned with, so we can go ahead and click
Apply (on the Properties tab of the Pipeline browser) to actually
load the data. At first, only a wire-frame cube will be displayed, which
shows the extents of the image data. To actually inspect the data, we
are going to change the drop-down list on the toolbar that currently displays
Outline to Points. This results in a display of a number of points
in space, as shown in Figure 15.
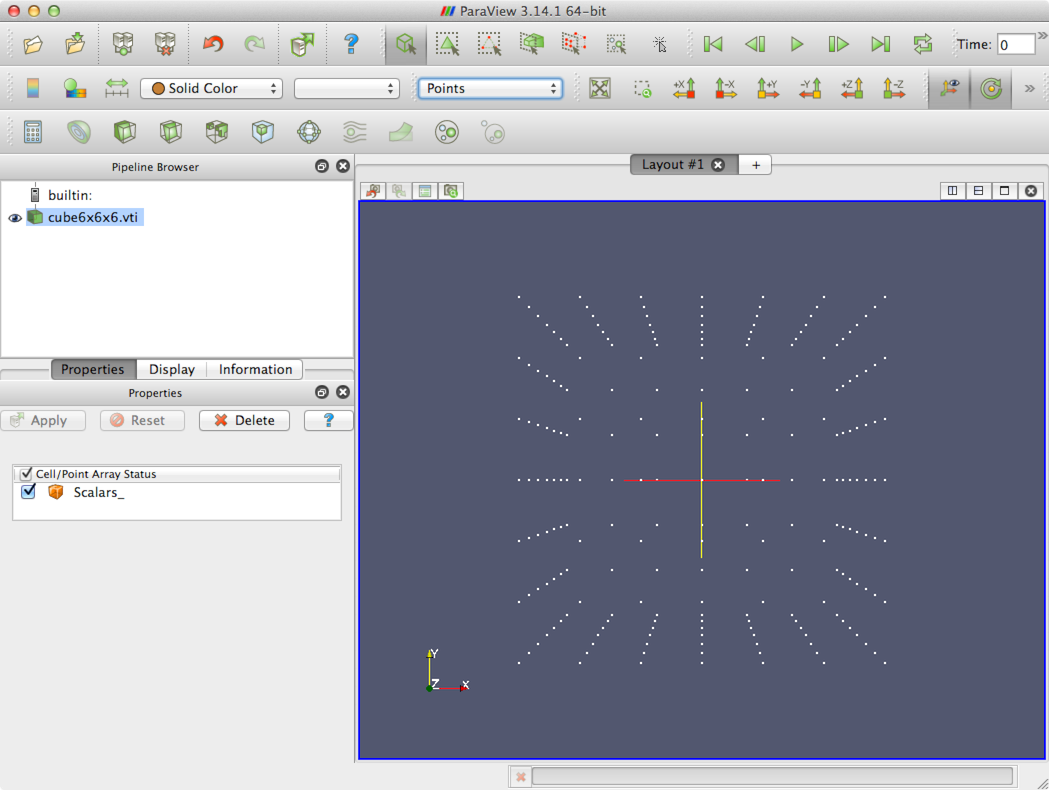
If you’re alert, you’ll notice that in fact there are 7×7×7 points. This is due to the fact that the actual data for this data file is associated with the Cells, to use VTK terminology, rather than the Points. The points shown are therefore in this case the corners of the cells. To make this clear, change the view again from Points to Surface with Edges. This will now look like Figure 16. (Click and drag in the image window of ParaView to rotate the object - experiment with both the right and left mouse buttons, and also while holding down any of the Shift, Control and Alt keys). We are going to create a finite element model where every Cell, or small constituent cube from Figure 16 will become one element in the finite element model.
For a simulated test, we are going to apply a compression test using n88modelgenerator to this data file. There are a
number of different standard compression tests, as described in
Standard Tests. Here we are going to use the axial
variation. In an axial compression
test, the sides are unconstrained and the top and bottom surfaces constrained
laterally, as if they experience a high contact friction with the
imaginary surfaces applying the compression.
7.1.1. Generating the model
The first step is to open a Terminal (on Windows a Command Prompt or PowerShell).
Make sure both that the Faim is on the Path, as described in How to run the solvers,
and also that you have activated the Anaconda python environment for n88tools,
as described in Install n88tools and vtkbone.
|
|
If you close the terminal part way through this tutorial, and then pick it up again later by opening a new terminal, you will have to re-set the environment variables and re-activate the conda environment. |
Assuming that you have copied the data file cube6x6x6.vti to your current
working directory, the command to generate the model is
n88modelgenerator --test=axial cube6x6x6.vti
Since we haven’t specified otherwise, n88modelgenerator will select all
default parameters, including default material properties (homogeneous
material with isotropic Young’s modulus of 6829 MPa and Poisson’s ratio 0.3),
and a displacement,
applied to the top surface in the z direction, numerically equivalent to
an apparent level strain of -0.01 (the minus indicates compressive strain).
Refer to the section on
n88modelgenerator for details on setting parameters differently if you wish
to do so.
Here is the output when we run it:
n88modelgenerator Version 9.0
Copyright (c) 2010-2020, Numerics88 Solutions Ltd.
Licensed to Numerics88 Solutions Ltd.; lic. no. 91
input_file = cube6x6x6.vti
output_file = cube6x6x6_axial.n88model
connectivity_filter = on
test = axial
test_axis = z
normal_strain = -0.01
top_surface = intersection
bottom_surface = intersection
material_table = homogeneous
youngs_modulus = 6829
poissons_ratio = 0.3
0.00 Reading input data.
0.02 Read 343 points.
0.02 Image bounds:
0.0000 6.0000 0.0000 6.0000 0.0000 6.0000
0.02 Applying connectivity filter.
0.02 Masked out 0 unconnected voxels.
0.02 Converting to hexahedral mesh.
0.02 Generated 216 hexahedrons.
0.02 Constructing material table.
0.02 Material table has 1 entry.
0.02 Constructing finite element model.
0.02 Model bounds:
0.0000 6.0000 0.0000 6.0000 0.0000 6.0000
0.02 Generated the following constraints:
bottom_fixed : 147 nodes
top_fixed : 98 nodes
top_displacement : 49 nodes
0.02 Writing Numerics88 Model file cube6x6x6_axial.n88model .
0.03 Done.
We now have a file cube6x6x6_axial.n88model that can be used directly as
input to the solver.
7.1.2. Solving the model
Having now defined the problem, we can solve it, and do some post-processing, all in one step with faim.
faim cube6x6x6_axial.n88model
The output is:
Model has 216 elements.
Model contains only linear material definitions.
Choosing n88solver_slt.
Running solver: n88solver_slt cube6x6x6_axial.n88model
n88solver_slt version 9.0
Copyright (c) 2010-2020, Numerics88 Solutions Ltd.
Licensed to Numerics88 Solutions Ltd.; lic. no. 91
Problem:
active solution = (none)
active problem = Problem1
number of elements = 216
number of nodes = 343
Solver engine:
engine = mt
precision = double
threads = 1
Convergence parameters:
convergence measure = set
convergence tolerance = 1e-06
convergence window = 16
maximum iterations = 30000
time (s) iter conv
0.0 30 5.4E-07
Convergence measure tolerance reached.
Number of linear iterations = 30
Peak data allocation : 75.8 kiB
Running field calculator: n88derivedfields cube6x6x6_axial.n88model
n88derivedfields version 9.0
Copyright (c) 2010-2020, Numerics88 Solutions Ltd.
Licensed to Numerics88 Solutions Ltd.; lic. no. 91
Problem:
active solution = Solution1
active problem = Problem1
number of elements = 216
number of nodes = 343
Solver engine:
precision = single
Peak data allocation: 19.8 kiB
Running analysis tool: n88postfaim --output_file cube6x6x6_axial_analysis.txt cube6x6x6_axial.n88model
7.1.3. Visualizing the results with ParaView
First ensure that ParaView is set up with the plugins to read Numerics88
files, as described in Installing and using the Numerics88 plugins for ParaView. Assuming that the plugins are loaded correctly,
cube6x6x6_axial.n88model can be opened directly with ParaView. When we
first open this file, it looks very similar to the
input data. However, if we go to the Information tab in the Pipeline
Browser, we can see that there are now several Data Arrays, Displacement,
ReactionForce, etc… as shown in Figure 17. Notice that the
icon next the the array name indicates whether the data is on Points
or Cells, which is equivalent in finite element terminology to Nodes and
Elements, respectively.
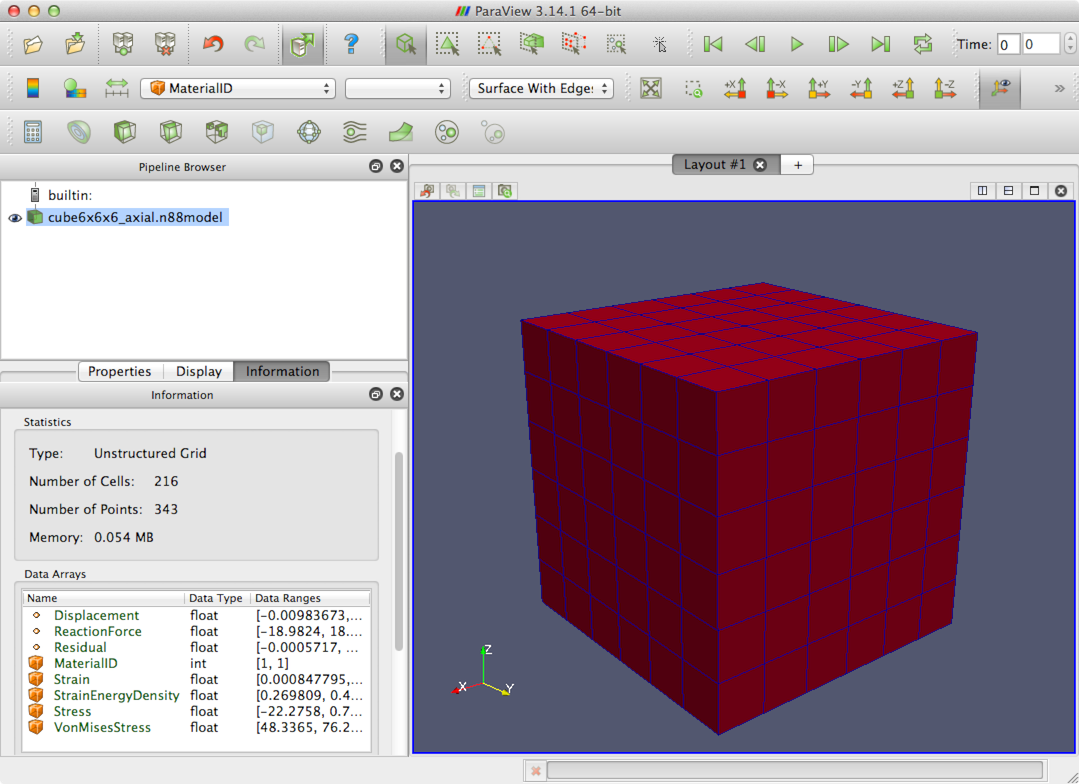
There are many ways to visualize the data. As a simple example, choose Displacement from the drop-down menu on the toolbar that currently shows _MaterialID. Also click the Toggle Color Legend Visibility button on the toolbar (on the very left side). ParaView should now look like Figure 18. Notice that a new drop-down box appears that shows Magnitude. This occurs because the Displacements are a vector quantity. Experiment with changing this to Z, X and Y.
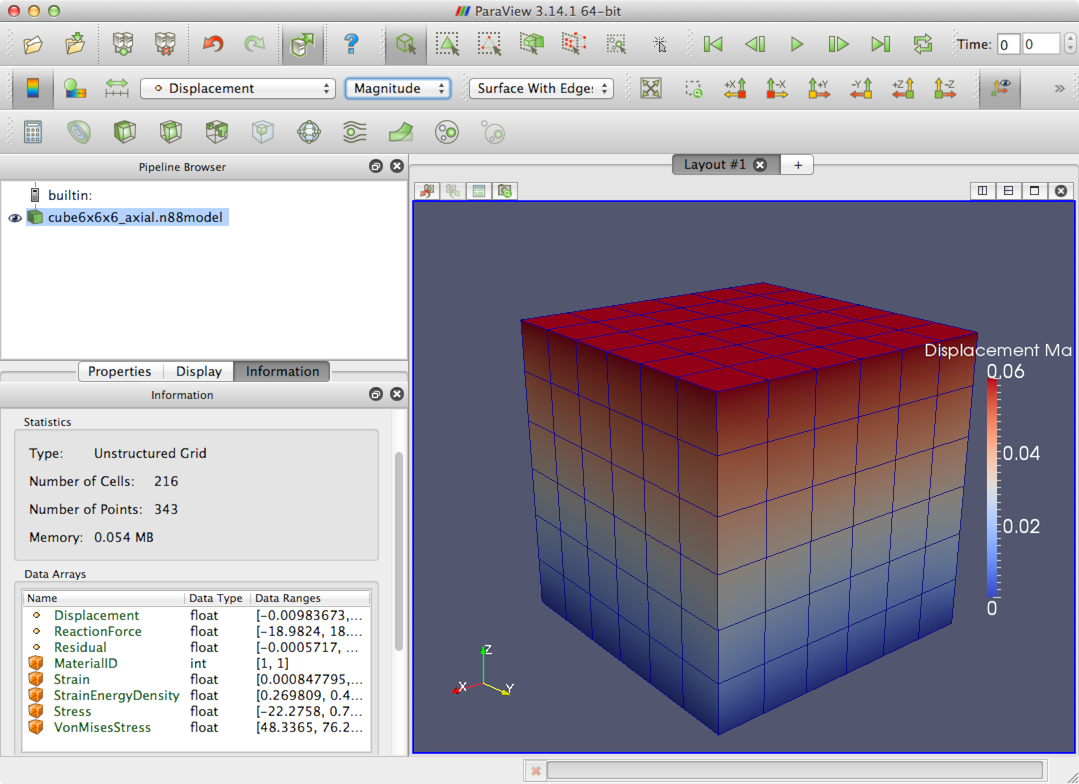
Although we now have the cube colored by Displacement, the object is shown
in its undeformed unloaded shape. To visualize the deformations, we can use
the Warp By Vector tool. There is an icon for this on the bottom
Toolbar. Because we have imposed a small strain, -0.01, it will be hard to
see. The Warp By Vector tool however allows us to apply a Scale Factor.
We will set this to 10, so that the displacements are amplified by a factor
of 10. The results are shown in Figure 19, where the compression
and outward bulging of the sides are clearly seen. In this figure, we
have, in addition to applying the Warp By Vector tool, re-enabled
the display of the original cube6x6x6_axial.n88model, which was
automatically disabled by ParaView when we connected a filter object to it.
We then set its display type to Outline, resulting in the white
box outline in Figure 19, which indicates the original undeformed
box shape.
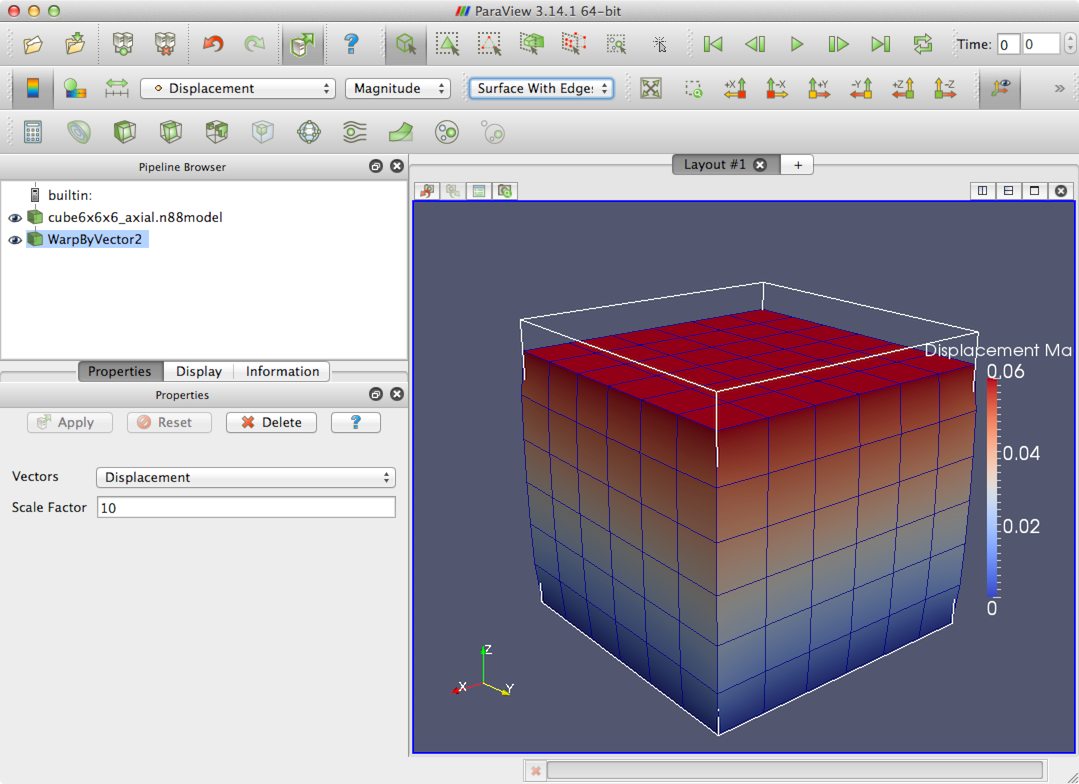
7.1.4. Obtaining numerical values from the analysis file
A typical result we want to obtain with a compression test is the object
apparent stiffness. Numerically the stiffness is the net external force
divided by the displacement. We can find the displacement and force on the top
surface from the analysis file, cube6x6x6_axial_analysis.txt. This file is
a text file, and can be opened with any text
editor. Refer to the section on post-processing with n88postfaim
for the complete explanation of the values available.
The displacement is obtained from table Nodal Displacements. The displacements in this table are listed according to node set.
n88modelgenerator has defined some standard node sets (for a complete
list see Creating node and element sets in the chapter
on Preparing Models with vtkbone.) Here the node sets that are relevant
are the two surfaces to which the boundary conditions are applied, namely
the top and bottom surfaces, face_z1 and face_z0, respectively.
The analysis file has been generated using these two node sets.
If we examine the Nodal Displacements table of
cube6x6x6x_axial_analysis.txt, as shown in Figure 20, we see
that the top node set has a uniform displacement in the z direction of
-0.06 mm. The relevant number is circled in red. Notice also that the
minimum and maximum are the same so all nodes of this set are equally
displaced, as we expect, since this is in fact a boundary
condition. The other node set is the nodes of the bottom
surface, and it has constant displacement of 0.
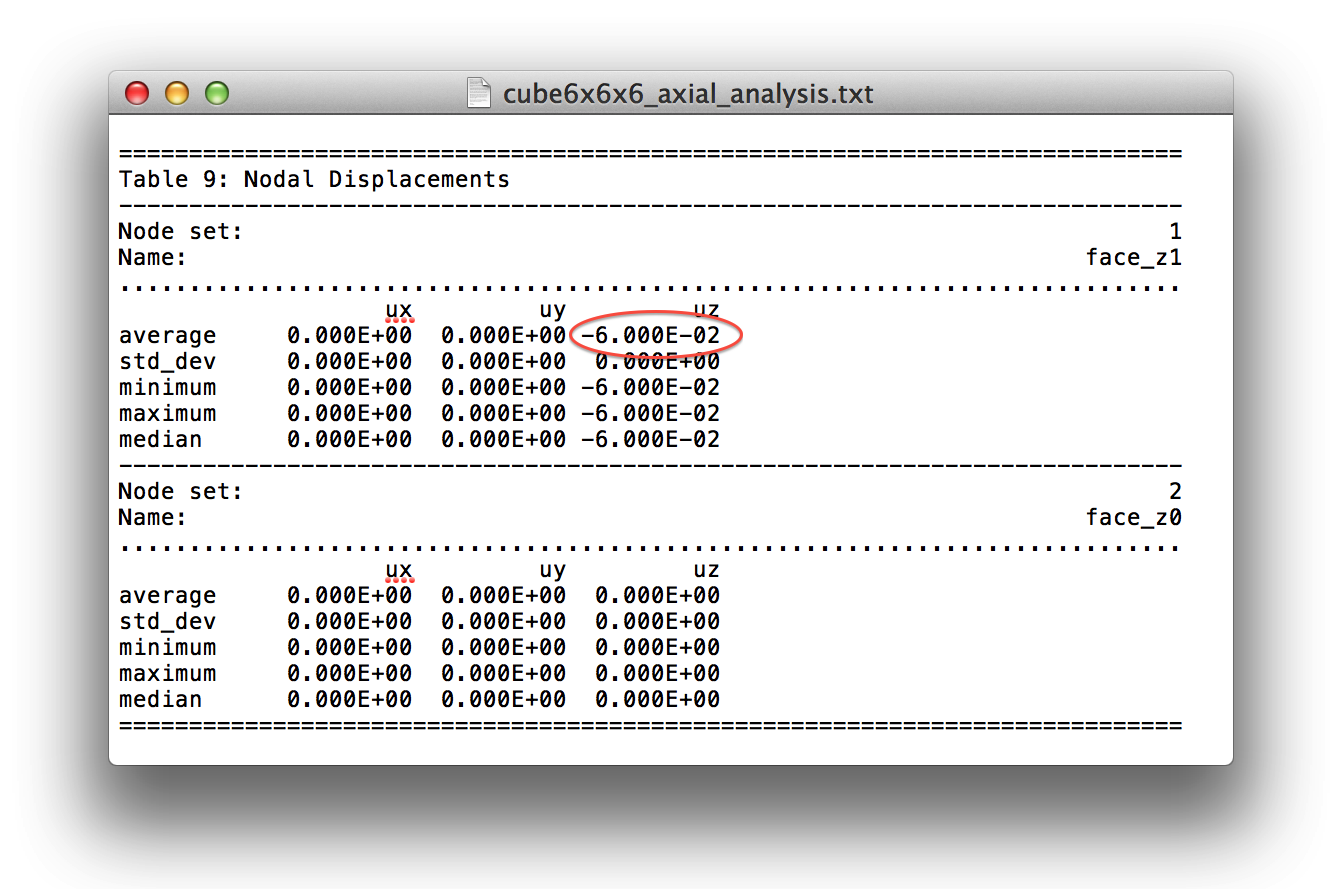
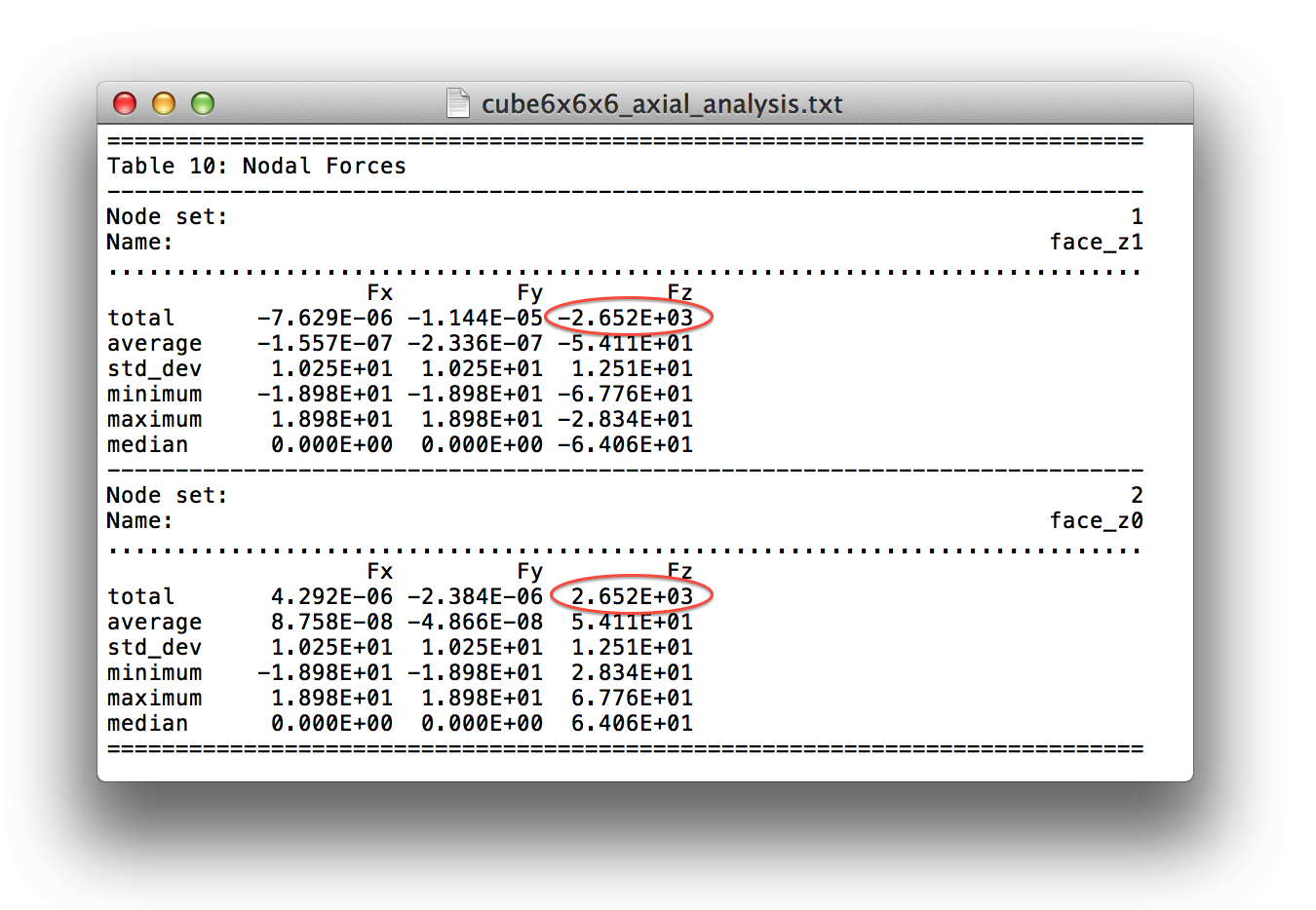
Similarly to the table for displacements, table Nodal Forces shows forces, summed over the defined node sets. Here the relevant value is -2651 N, as shown in Figure 21. The apparent stiffness of the cube is therefore
Is this value reasonable? We can estimate what we should get. Completely ignoring lateral expansion and Poisson’s ratio, we can do a quick estimate that the stiffness of a homogeneous cube should be approximately,
This is close to what we obtained from the finite element model. The difference arises from the fact that the finite element model takes account of the complicated lateral expansion (bulging of the sides) that occurs in an axial test, while our simple back-of-the-envelope calculation assumes uniaxial conditions (i.e., no lateral constraint on the top and bottom boundary surfaces).
This concludes the cube tutorial. You have learned how
to generate standard models from image data using n88modelgenerator,
how to solve the models, how to visualize the models using ParaView,
and how to do some elementary post-processing analysis.
7.2. Tutorial: Compression test of a radius bone slice
In the previous tutorial, we saw how to generate a finite element model from an image file using n88modelgenerator, how to solve it, how to visualize the results, and how obtain some relevant numerical results. In this tutorial, we are going to generate and solve a similar compression test. Instead of a small contrived image, we will be using a real data file obtained from a microCT scan of a distal radius bone. We will also provide more detail about the steps along the way, and be introduced to some of the tools that aid in examining and verifying models.
In detail, this tutorial will demonstrate:
-
How to use n88modelinfo to obtain information about
n88modelfiles, and in particular to trace back exactly how they were generated and processed. -
How to examine the residuals to evaluate the accuracy of the solution.
-
How to quantify the load sharing between the two types of bone, cortical bone and trabecular bone.
-
How to compress data files using n88copymodel for efficient storage.
The data file is radius_slice82.aim, and it is obtained with the tutorial
data available from http://numerics88.com/downloads/ .
This is a large image file of
325×437×110 voxels in size. It was obtained with a scan
resolution of 82 micrometers. The tutorial will be demonstrated using
this data file. However, a reduced-resolution file, radius_slice164.aim, is
also provided. The resolution has been reduced to an effective 164 micrometers,
resulting in a much smaller data file with dimensions 163×219×55.
If you are working on a computer with limited memory, or are just impatient, then you can follow along using the smaller file.
Before proceeding, ensure that the Numerics88 plugins for ParaView are loaded as described in Install the Numerics88 plugins for ParaView.
In the previous tutorial you might recall that the data file was a VTK image data file, and that it explicitly had the data on the Cells rather than on the Points. Most image file formats make no such distinction, but ParaView always uses one or the other, as it affects how the data are rendered. In fact if you experiment you will determine that certain filters will work in one case and not the other, or that other filters will work differently depending on whether the data are on the Points or the Cells. As an example, the Contour filter requires data on the Points, while the Threshold filter generally only gives the results you expect with the data on the Cells. You will see when opening an AIM file that in the Properties tab we have a couple of options, which are Data on Cells and Pad. This is shown in Figure 22. For this tutorial we want to select Data on Cells, which is the default.
Once you’ve opened the file radius_slice82.aim (or radius_slice164.aim)
and clicked Apply, locate the icon for the Threshold filter on the toolbar.
Change the Lower Threshold to 1 before clicking Apply, as shown in
Figure 23; Scalars should be set to AIMData.
Now change the Representation drop-down box to Surface and the Color by drop-down box to AIMData. Also turn on the legend by clicking the Toggle Color Legend Visibility button. After rotating the image (click and drag in the image window) to get a good viewing angle, this should look something like Figure 24. You can see that this data file has been segmented such that the cortical bone has material ID 127 and the trabecular bone has material ID 100.
7.2.1. Generating the model
As before, we recommend copying the data file radius_slice82.aim into a
temporary working directory. The command to generate the model is
n88modelgenerator --test=uniaxial radius_slice82.aim
The resulting model file will be named radius_slice82_uniaxial.n88model.
|
|
Don’t forget that before running n88modelgenerator, make sure that
Faim is on the Path, as described in How to run the solvers,
and also that you have activated the Anaconda python environment for n88tools,
as described in Install n88tools and vtkbone.
|
Before we solve it, we are going to examine this model file using n88modelinfo. You will find that n88modelinfo is a very useful tool for getting information about the models, and for tracing back how they were created and solved. n88modelinfo can be run like this,
n88modelinfo radius_slice82_uniaxial.n88model
n88modelinfo can generate quite a bit of output. We will shortly see how to reduce this to just the information that we are interested in. For now though, let’s look at the complete output. Comments follow below the example output.
History:
----------------------------------------------------------------------
2016-Sep-15 14:49:17 Model created by n88modelgenerator version 8.0
----------------------------------------------------------------------
Log:
----------------------------------------------------------------------
2016-Sep-15 14:49:17
n88modelgenerator Version 8.0
Copyright (c) 2010-2016, Numerics88 Solutions Ltd.
Licensed to Numerics88 Solutions Ltd.; lic. no. 91
input_file = radius_slice82.aim
output_file = radius_slice82_uniaxial.n88model
connectivity_filter = on
test = uniaxial
test_axis = z
normal_strain = -0.01
pin = off
top_surface = intersection
bottom_surface = intersection
material_table = homogeneous
youngs_modulus = 6829
poissons_ratio = 0.3
0.02 Reading input data.
0.05 Read 15849468 points.
0.05 Image bounds:
49.6920 76.3420 38.7040 74.5380 0.0000 9.0200
0.05 Applying connectivity filter.
0.66 Masked out 0 unconnected voxels.
0.66 Converting to hexahedral mesh.
1.56 Generated 2667590 hexahedrons.
1.56 Constructing material table.
1.86 Material table has 2 entries.
1.86 Constructing finite element model.
5.17 Model bounds:
50.1020 76.0960 39.1140 74.2100 0.0000 9.0200
5.17 Generated the following constraints:
bottom_fixed : 40032 nodes
top_displacement : 25991 nodes
----------------------------------------------------------------------
Active Settings:
----------------------------------------------------------------------
Active Solution : None
Active Problem : Problem1
Active Part : Part1
----------------------------------------------------------------------
Materials:
----------------------------------------------------------------------
Name : NewMaterial1
Type : LinearIsotropic
E : 6829.0
nu : 0.3
----------------------------------------------------------------------
Parts:
----------------------------------------------------------------------
Name : Part1
NumberOfNodes : 3816642
Hexahedrons :
NumberOfNodesPerElement : 8
NumberOfElements : 2667590
----------------------------------------------------------------------
Constraints:
----------------------------------------------------------------------
Name : bottom_fixed
Part : Part1
Type : NodeAxisDisplacement
NumberOfValues : 40032
Name : top_displacement
Part : Part1
Type : NodeAxisDisplacement
NumberOfValues : 25991
Name : convergence_set
Part : Part1
Type : NodeAxisForce
NumberOfValues : 25991
----------------------------------------------------------------------
NodeSets:
----------------------------------------------------------------------
Name : face_z0
Part : Part1
NumberOfNodes : 40032
Name : face_z1
Part : Part1
NumberOfNodes : 25991
Name : face_x0
Part : Part1
NumberOfNodes : 15
Name : face_x1
Part : Part1
NumberOfNodes : 14
Name : face_y0
Part : Part1
NumberOfNodes : 27
Name : face_y1
Part : Part1
NumberOfNodes : 17
----------------------------------------------------------------------
ElementSets:
----------------------------------------------------------------------
Name : face_z0
Part : Part1
NumberOfElements : 28999
Name : face_z1
Part : Part1
NumberOfElements : 21210
Name : face_x0
Part : Part1
NumberOfElements : 8
Name : face_x1
Part : Part1
NumberOfElements : 6
Name : face_y0
Part : Part1
NumberOfElements : 12
Name : face_y1
Part : Part1
NumberOfElements : 8
----------------------------------------------------------------------
Problems:
----------------------------------------------------------------------
Name : Problem1
Part : Part1
Constraints : bottom_fixed,top_displacement
ConvergenceSet : convergence_set
PostProcessingNodeSets : face_z1,face_z0
PostProcessingElementSets : face_z1,face_z0
----------------------------------------------------------------------
Solutions:
----------------------------------------------------------------------
----------------------------------------------------------------------
Some things to note about the output of n88modelinfo:
-
The History is a useful field to see what programs were run to generate or modify the file, and when.
-
The Log field is similar to the History, except that it gives far more detailed information. Of particular note is that n88modelgenerator reports its complete configuration, including all parameters values relevant to the particular test type, even ones which haven’t been explicitly set, but are default values.
-
This file hasn’t been solved yet, so there is nothing in Solutions.
-
The sets defined for post-processing are face_z1 and face_z0, which are the top and bottom surfaces, respectively. We will need this information later to interpret the results in the analysis file.
Now, as mentioned, that is a lot of output. Often we are interested in just part of the output. In this case, we can specify the bits we want. For example, to get just the History and the Log, we could do this,
n88modelinfo --history --log radius_slice82_uniaxial.n88model
|
|
To discover what the valid arguments to n88modelinfo are,
you can either refer to the manual (See n88modelinfo), or you can
run n88modelinfo --help.
|
|
|
If you want the output of n88modelinfo to be saved in a file, then run it like this n88modelinfo radius_slice82_uniaxial.n88model > info.txt This will direct the output of n88modelinfo to
the file |
7.2.2. Solving the model
From the previous tutorial, we know that we can use faim to solve the model and perform so post-processing on it. faim itself actually just calls three other programs to carry out the actual work. Usually it’s easiest to call faim, but in this tutorial we are going to call the individual processing programs ourselves, so we can understand what faim is doing.
The first step carried out by faim is to solve the model with n88solver_slt, which we can do with
n88solver_slt radius_slice82_uniaxial.n88model
The specification slt for the solver means that this is the solver for small strain, linear problems, using a material table. |
|
|
This model will take some time to solve. If you have licensed the GPU solvers, and have suitable hardware, then you probably would like to jump right into using the GPU hardware. To do this, specify the engine and device. For example, for a system with two compute-capable Nvidia cards, including the one being used for the display, the command would be: n88solver_slt --engine=nv --device=0,1 radius_slice82_uniaxial.n88model If you have a system where the compute GPUs are distinct from the
video card used for the display, such as is typical for Nvidia Tesla hardware,
then the correct device option for two
compute-capable Nvidia cards is more likely to be |
We can see how this has modified the n88model file by running
n88modelinfo again. To avoid the lengthy complete output,
here we use arguments that show only the sections
that have in fact changed
n88modelinfo --history --log --solutions radius_slice82_uniaxial.n88model
The output is:
History:
----------------------------------------------------------------------
2016-Sep-15 14:49:17 Model created by n88modelgenerator version 8.0
2016-Sep-15 15:22:54 Solved by n88solver_slt 8.0
----------------------------------------------------------------------
Log:
----------------------------------------------------------------------
2016-Sep-15 14:49:17
n88modelgenerator Version 8.0
Copyright (c) 2010-2016, Numerics88 Solutions Ltd.
Licensed to Numerics88 Solutions Ltd.; lic. no. 91
input_file = radius_slice82.aim
output_file = radius_slice82_uniaxial.n88model
connectivity_filter = on
test = uniaxial
test_axis = z
normal_strain = -0.01
pin = off
top_surface = intersection
bottom_surface = intersection
material_table = homogeneous
youngs_modulus = 6829
poissons_ratio = 0.3
0.02 Reading input data.
0.05 Read 15849468 points.
0.05 Image bounds:
49.6920 76.3420 38.7040 74.5380 0.0000 9.0200
0.05 Applying connectivity filter.
0.66 Masked out 0 unconnected voxels.
0.66 Converting to hexahedral mesh.
1.56 Generated 2667590 hexahedrons.
1.56 Constructing material table.
1.86 Material table has 2 entries.
1.86 Constructing finite element model.
5.17 Model bounds:
50.1020 76.0960 39.1140 74.2100 0.0000 9.0200
5.17 Generated the following constraints:
bottom_fixed : 40032 nodes
top_displacement : 25991 nodes
2016-Sep-15 15:22:54
n88solver_slt version 8.0
Copyright (c) 2010-2015, Numerics88 Solutions Ltd.
Licensed to Numerics88 Solutions Ltd.; lic. no. 91
Problem:
active solution = (none)
active problem = Problem1
number of elements = 2667590
number of nodes = 3816642
Solver engine:
engine = nv
precision = double
devices = 0
Convergence parameters:
convergence measure = set
convergence tolerance = 1e-06
convergence window = 312
maximum iterations = 30000
Convergence measure tolerance reached.
Number of linear iterations = 2761
Peak data allocation (system, device): 872 MiB, 692 MiB
----------------------------------------------------------------------
Solutions:
----------------------------------------------------------------------
Name : Solution1
Problem : Problem1
Variables defined on nodes:
Displacement
----------------------------------------------------------------------
Note things are worth noting here. In the Log section, we now have a record of the complete configuration of the solver (in this case, it happens to be default values). And in the Solutions section, we now have a solution (“Solution1”) with a field defined on the nodes, namely Displacements.
7.2.3. Evaluating the accuracy of the solution
Faim includes a tool that can be used to evaluate the accuracy of the obtained solutions. This is discussed in the section Evaluating solution quality. It can be run like this:
n88evaluate radius_slice82_uniaxial.n88model
|
|
The n88evaluate tool in its current implementation requires
far more memory than the solver itself does. For this example, it will
use almost 60GB of memory, while the solver needed less than 2GB. Therefore,
currently, you should not attempt to run this part of the tutorial on a machine
with less than 64GB of RAM .
|
The output is,
Analysis of solution displacements at boundary conditions:
max err : 0.00E+00
rms err : 0.00E+00
Analysis of forces (residuals):
max err : 1.28E-05
rms err : 9.35E-07
max err/max force : 9.26E-06
rms err/max force : 6.79E-07
The meaning of these results is discussed in the section
Evaluating solution quality;
briefly we can take the number rms err/max force as a measure
of the relative error. Here it is 7×10-7, which is acceptably small.
7.2.4. Obtaining additional solution fields with n88derivedfields
So far our solution consists only of displacements. Many other values are of interest, for example strains and stresses. These are calculated with n88derivedfields. It can be run very simply as,
n88derivedfields radius_slice82_uniaxial.n88model
Now let’s have a look at what’s in the model file, using again n88modelinfo,
n88modelinfo --history --solutions radius_slice82_uniaxial.n88model
The output is:
History:
----------------------------------------------------------------------
2016-Sep-15 14:49:17 Model created by n88modelgenerator version 8.0
2016-Sep-15 15:22:54 Solved by n88solver_slt 8.0
2016-Sep-15 15:27:58 Processed by n88derivedfields 8.0
----------------------------------------------------------------------
Solutions:
----------------------------------------------------------------------
Name : Solution1
Problem : Problem1
Variables defined on nodes:
Displacement
ReactionForce
Variables defined on elements:
Strain
Stress
StrainEnergyDensity
VonMisesStress
----------------------------------------------------------------------
We have a number of new solution fields (or variables). Some are defined on the nodes and some defined on the elements. For details on these fields, see n88derivedfields.
|
|
Even if you are not interested in the numerical values of the fields added by n88derivedfields, they are required by n88postfaim. Running the latter requires first running the former. |
7.2.5. Using n88postfaim to generate the analysis file
The final step performed by faim is to call n88postfaim,
which does post-processing analysis. In the previous
tutorial we saw that an analysis file was generated, which is a text
file with a number of tables summarizing the numerical results.
It is n88postfaim that generates this text file. To run
it on an n88model file that contains all the solution fields is
once again straightforward in most cases,
n88postfaim -o analysis.txt radius_slice82_uniaxial.n88model
Note that unlike the previous commands, for n88postfaim
we actually have to specify an output file with -o analysis.txt.
(If we don’t, then the output will just be printed to the terminal.)
The faim command, which combines n88solver_slt, n88derivedfields,
and n88postfaim, would have automatically generated the filename
radius_slice82_uniaxial_analysis.txt in this case, but that is
getting a little bit lengthy, so we’ll just use analysis.txt here.
7.2.6. Determining load sharing distribution with n88postfaim
We already saw some of the values in the analysis file in the previous
tutorial. For this tutorial, we are going to have a look at table
Load Sharing, as shown in
Figure 25. We see that this table breaks up the
total load on each node set according to material ID. In this case,
we have material ID 127 being cortical bone, and material ID 100 being
trabecular bone. Recall that the material properties are not different; it is
merely a different labelling. Here we will see the reason for doing this.
Recall also that the sets defined for post-processing are the
top and the bottom surfaces. (If you’re not sure of this then the command
n88modelinfo --problems radius_slice82_uniaxial.n88model will show you.)
Because of the alignment in the CT scanner, in this case the top surface
is proximal, and the bottom surface is distal.
Referring to the values circled in red in Figure 25, we
conclude that on the proximal surface of this radius bone slice, the
proportion of the load carried by
the trabecular bone is (-806) / (-5199) = 15.5%, while on the distal
surface of the slice the proportion of the load carried by
the trabecular bone is (3637) / (5199) = 70.0%.
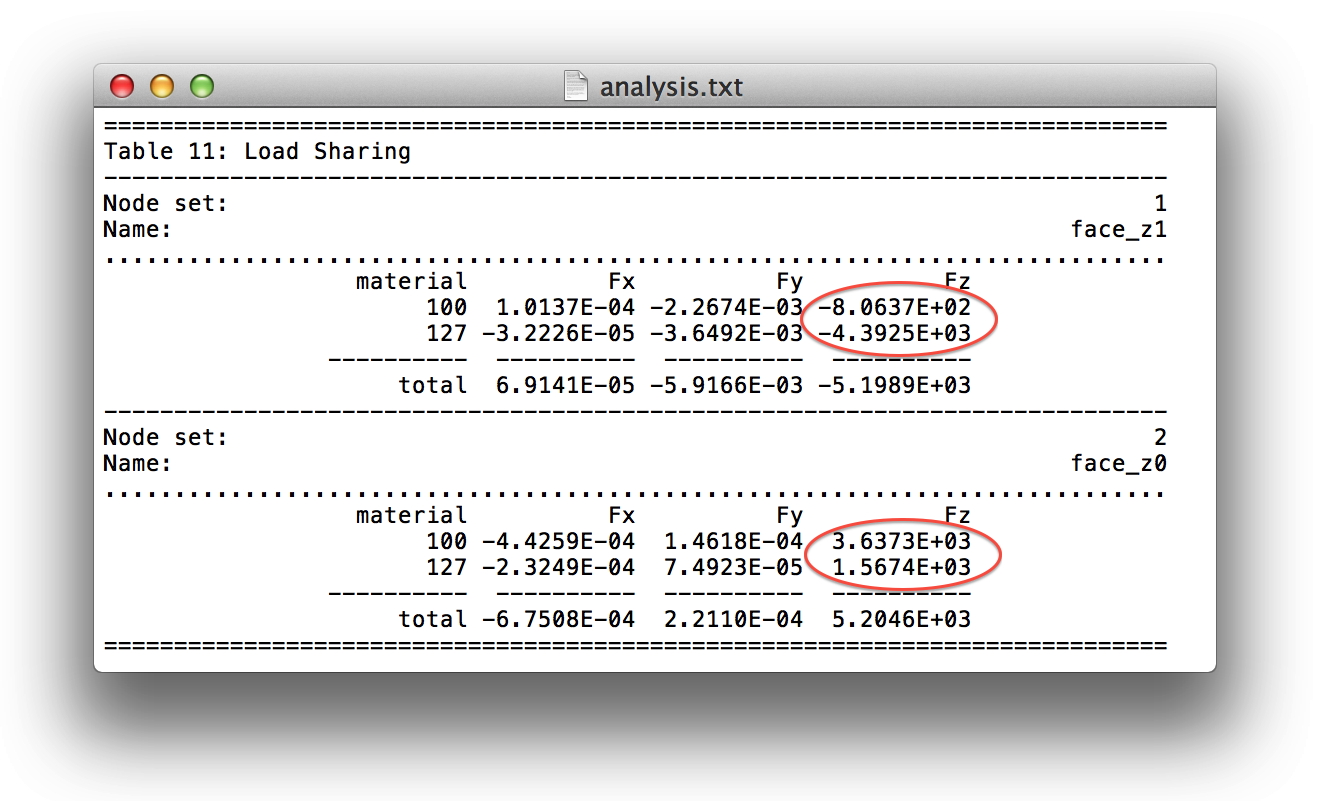
7.2.7. Enabling compression for large model files
The n88model file format supports compression internally and transparently.
An n88model which contains compressed data can be read with every N88 tool just like
any other n88model, without the need for the user to explicitly
de-compress the data. Compression is not used by default, because it
does have an increased calculation overhead for reading and writing
(particularly for writing). However, once we are finished with processing
the model, we typically want to keep the data around for archival
purposes. It is recommended to compress the n88model files for archiving.
This can be done with the n88compress tool, as follows,
n88compress radius_slice82_uniaxial.n88model
For this data file, enabling compression reduces its size from 438 MB to 226 MB, a reduction of 47%.
This ends the tutorial on a compression test on a radius bone slice. We
were introduced to n88modelinfo, we solved a realistic
model, we looked at using the residuals to evaluate the quality of the
solution, we saw how to do load distribution calculations, and finally we
learned how to enable compression to more efficiently
store large n88model files.
7.3. Tutorial: Bending test of a radius bone with an uneven surface
In the previous two tutorials, we had input images where the object in the image intersected the top and bottom bounds of the image, thus forming nice flat surfaces to which we could apply boundary conditions. This won’t always be the case. In this tutorial we’ll look at an object with a very uneven surface.
In detail, this tutorial will demonstrate:
-
How to use the uneven surface parameters of n88modelgenerator.
-
How to use n88extractsets to examine our boundary conditions.
The data file is radius82.aim. As for the previous tutorial, there
is also a reduced resolution version, radius164.aim. This data
is particularly large, with the unreduced version having a
size of 400×350×1100, or 154 million voxels; the resulting
finite element model will have 14 million elements.
The input image is shown in Figure 26.
|
|
In this tutorial, we are no longer going to go into detail on how to load and render data in ParaView, as we did in the previous two tutorials. If you’re curious about how we generated that image of the radius bone from the image file, these are the steps:
|
7.3.1. Generating the model with n88modelgenerator
We are going to apply a bending test, as described in Bending test. In order to identify the rough head of the bone as a boundary surface, we use the option bottom_surface=visible. As it implies, it will select nodes that are visible from a certain point of view. In this case, visible means “looking up from below” (effectively from an infinite distance, as parallel rays are used). Note that the distal head of the bone is in the “bottom” of the image, that is at smaller values of z. With this option, you can imagine that we might “see” parts of the object that are far away if they are not obscured by the foreground part of the image. We don’t want these distant parts of the object to form part of our boundary set, so when we use the bottom_surface=visible option, we nearly always want to set a depth limit as well using bottom_surface_maximum_depth. In this case a suitable limit is 15 (units are the same as the image units, which are millimeters in this case). In general there may be a bit of experimentation to get the best depth limit.
Since we have several parameters that we want to specify, it will be more
convenient to create a configuration file for
n88modelgenerator than to specify them individually
on the command line, as we have done previously. To do this, open
a text editor, and create the following file. Save it to your working
directory as radius_bending_test.conf.
# File: radius_bending_test.conf # # A configuration file for the radius bending tutorial. input_file = radius82.aim test = bending bottom_surface = visible bottom_surface_maximum_depth = 15
Lines starting with # are comment lines: any line starting with # is ignored.
We can now run n88modelgenerator by specifying only the configuration file to use:
n88modelgenerator --config radius_bending_test.conf
|
|
Some text editors automatically add a .txt file extension.
You can either
subsequently rename the file, or just accept the .txt ending and
everywhere in this tutorial use the actual complete file name. Even more
confusing can be that many operating systems by default hide the
file extension in the file browser, so that you may save a file as radius_bending_test.conf,
and the file browser in your operating system shows it with this name,
but its complete name is actually radius_bending_test.conf.txt. The
complete name must be specified to all Numerics88 tools.
|
7.3.2. Using n88extractsets to obtain and visualize boundary conditions
Because this is a non-trivial boundary set, we really want to visualize it to make sure it is reasonable and that it corresponds to what we expect. The best way to do this is with the tool n88extractsets. This is the command to use:
n88extractsets --constraints radius82_bending.n88model
Here “--constraints” means both boundary conditions and applied loads. (We can leave off this option, but then we will get even more output files which in the present case we are not interested in.)
The output looks like this:
Reading N88 Model file : radius82_bending.n88model Writing constraint : radius82_bending_constraint_bottom_fixed.vtp Writing constraint : radius82_bending_constraint_top_fixed.vtp Writing constraint : radius82_bending_constraint_top_displacement.vtp Writing constraint : radius82_bending_constraint_bottom_displacement.vtp
We see that four files are generated, one for each constraint.
These are VTK “PolyData” files, which consist of a set of “Vertices”
(points), one for each node in the boundary condition set.
n88modelgenerator has separated the “fixed” constraints,
which are degrees of freedom that are fixed at zero, and the
“displacement” constraints, which are degrees of freedom that are fixed
at some non-zero value. This distinction is sometimes useful, although
the solver does not require it. In this case the nodes belonging to
the constraint or boundary condition have x and y fixed at zero,
and z at non-zero values. Thus the “fixed” and “displacement” sets
will consist of the same set of nodes, but with different senses and
values. We are going to open the file radius82_bending_constraint_bottom_displacement.vtp
displacement and render it together with the contoured input image. This
is shown in Figure 27. Each individual
node belonging to the boundary condition is shown as a blue dot.

|
|
Generating this image is quite straightforward. We start with the
contoured input image data, as above, then we also open the file
|
This looks good so we can go ahead and solve this model with faim. Expect this to take a while - go grab a coffee.
faim radius82_bending.n88model
|
|
Just as in the previous model, if you have licensed the GPU solvers, and have suitable GPU hardware, then you are going to want to use it. faim can take all the arguments that n88solver can so for example: faim --engine=nv --device=0,1 radius82_bending.n88model where as before the device list will depend on the number of GPUs in your system and their configuration . |
As this is a very large file, once solved we should enable compression as in the previous tutorial. Compression can take a rather long time on a file this large. Remember that it is never necessary to uncompress an n88model file before reading it.
n88compress radius82_bending.n88model
A comparison of the original input image with the solved model is shown in Figure 28. Here we have used a Warp By Vector filter with a Scale Factor of 15 to make the distortion more evident to the eye.
|
|
Generating an attractive rendering of the solved model (or any
|
Another useful way to render this data is coloured by von Mises stress. See VonMisesStress. This is shown in Figure 29.
|
|
You will want to manually set the scale of the coloring for von Mises stress, as the uneven contact surface has locally very high stresses, which however are uninteresting (and even unphysical, as the microscopic contact surface irregularities would yield). You can adjust the range by selecting Color Map Editor from the View menu, then click on the Rescale to Custom Range button to the left of the color map plot. |
Showing the von Mises stress as in Figure 29 is informative, but only indicates the stress on the visible surfaces. Often we will want to look at the stresses within the volume. One way to do this is with a Slice filter. This is shown in Figure 30. Without going into a great deal of detail, you can see the filters used in this rendering in the Pipeline Browser.
|
|
The Slice filter should be used on volume data, and not on surface data. Notice that in Figure 29 we’ve applied the Slice filter to the output of WarpByVector1, and not to ExtractSurface1 or anything derived from it. |
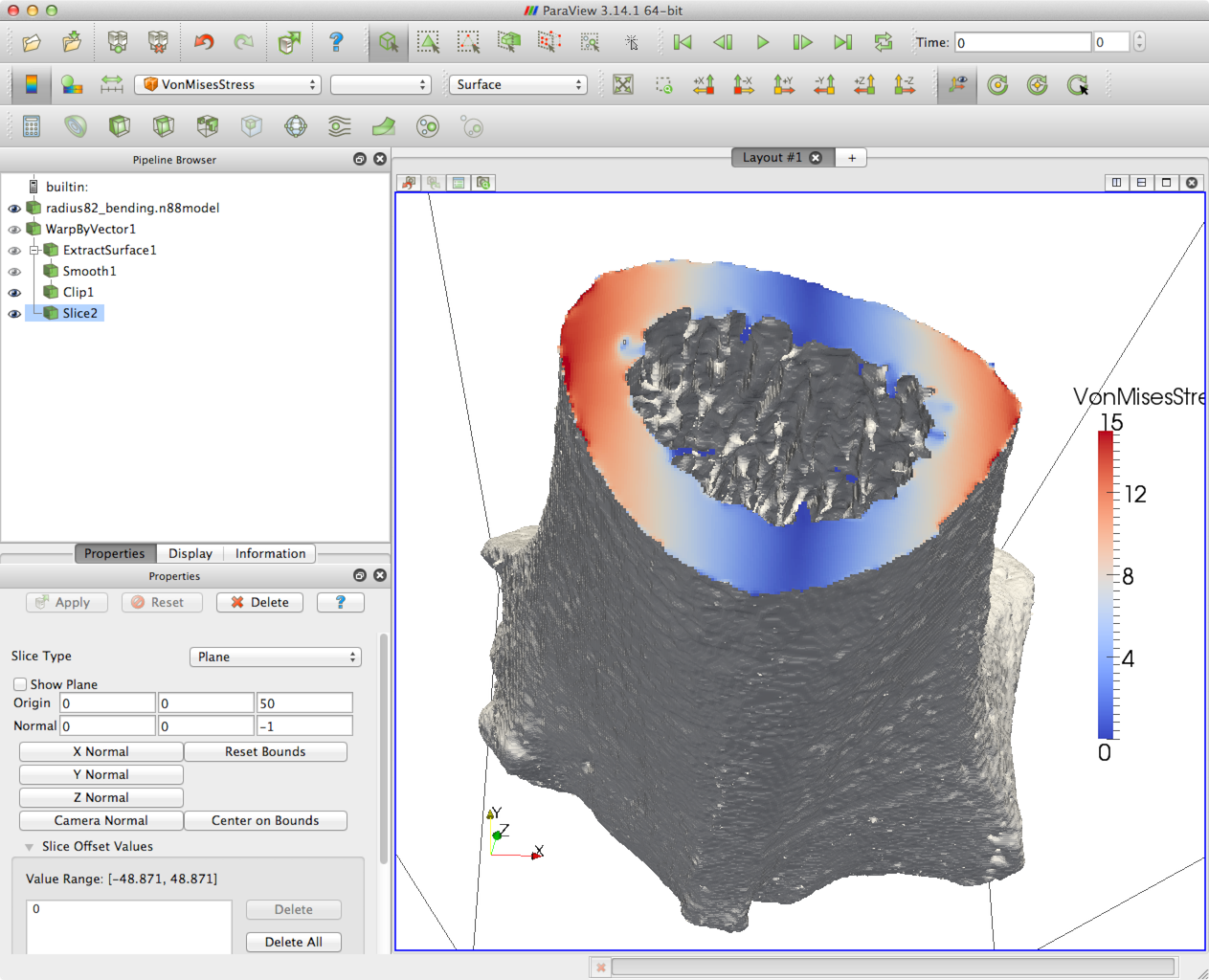
7.3.3. Numerical results
The interesting quantity in the analysis file
radius82_bending_analysis.txt (see the section on post-processing with n88postfaim) is the torque around
the bending axis, which in this case is in the y direction. Refer to
Figure 8. This quantity
is given as the total of Ty in the following table from
radius82_bending_analysis.txt. By default, this is calculated
around the center of mass of
the object, although you can re-run n88postfaim and
specify an argument for the argument rotation_center
if you want the torques calculated around an axis passing through a different
point. Because the head of the bone is “down”
in the sense of smaller z, face_z0 is the head of the bone, and
face_z1 is the cut face of the shaft. In any case, we can see that the torques
balance. The numerical value of the y compenent of the torque is
1997 N·mm (see A note about units), or 1.997 N·m.
============================================================================
Table 11: Nodal Torques
---------------------------------------------------------------------------
Torque measured relative to: 60.502 94.130 48.216
---------------------------------------------------------------------------
Node set: 1
Name: face_z1
............................................................................
Tx Ty Tz
total -1.213E+02 -1.997E+03 -1.928E+01
average -1.099E-02 -1.810E-01 -1.747E-03
std_dev 1.134E-01 1.252E-01 2.173E-02
minimum -6.034E-01 -5.249E-01 -9.884E-02
maximum 3.538E-01 4.623E-01 6.071E-02
median -8.431E-03 -1.915E-01 4.481E-05
---------------------------------------------------------------------------
Node set: 2
Name: face_z0
............................................................................
Tx Ty Tz
total 1.215E+02 1.996E+03 1.927E+01
average 1.601E-03 2.630E-02 2.538E-04
std_dev 1.591E+00 5.163E+00 9.762E-01
minimum -3.176E+01 -2.068E+01 -2.480E+01
maximum 2.722E+01 8.554E+01 2.405E+01
median -2.631E-02 -7.920E-01 -1.935E-02
============================================================================
7.4. Tutorial: Radius bending with elasto-plastic material properties
In this tutorial, we are going to repeat the radius bending test of the previous tutorial, but this time we will use nonlinear elasto-plastic material properties. We recommend that you first read the section on Plasticity.
7.4.1. Creating the model
Because nonlinear models take substantially longer to solve than
linear models, for this tutorial we are going to use the
reduced-resolution image file radius164.aim. However, if you
have the processing power and the time to obtain solutions, and
you want to use the original resolution file radius82.aim, you
can of course do so.
Creating a model with elasto-plastic material properties with
n88modelgenerator is straight-forward: one simply has to set the
plasticity option. For example, the
following configuration file is similar to the one in the last tutorial,
but we have added plasticity = vonmises,10. This means that we
want a von Mises yield criterion (see von Mises yield criterion) with a yield strength of 10 MPa. There
is no scientific justification for choosing this numerical value
for the yield strength: it was chosen simply because it produces
interesting results for this tutorial.
# File: radius_bending_elastoplastic.conf # # A configuration file for the tutorial: radius bending with # elasto-plastic material properties. input_file = radius164.aim output_file = radius_bending_elastoplastic.n88model test = bending bottom_surface = visible bottom_surface_maximum_depth = 15 plasticity = vonmises,10
As before, we generate the model with
n88modelgenerator --config radius_bending_elastoplastic.conf
We can verify that the resulting model file has elasto-plastic material definitions using the handy n88modelinfo command,
n88modelinfo --materials radius_bending_elastoplastic.n88model
The output is
Materials: ---------------------------------------------------------------------- Name : NewMaterial1 Type : VonMisesIsotropic E : 6829.0 nu : 0.3 Y : 10.0 ----------------------------------------------------------------------
7.4.2. Solving the model
We can solve the model with faim,
faim radius_bending_elastoplastic.n88model
|
|
Let us look into the file to see what fields are present for a solved elasto-plastic model. The command to list the solutions is, as before,
n88modelinfo --solutions radius_bending_elastoplastic.n88model
this gives an output of
Solutions:
----------------------------------------------------------------------
Name : Solution1
Problem : Problem1
Variables defined on nodes:
Displacement
ReactionForce
Variables defined on elements:
PlasticStrain
Strain
Stress
StrainEnergyDensity
VonMisesStress
Variables defined on gauss points:
PlasticStrain
----------------------------------------------------------------------
Everything here is as before for linear solutions, with the addition
of a new field PlasticStrain. PlasticStrain is the irreversible strain
that arises from exceeding the elastic limits as defined by the yield
surface.
See PlasticStrain in the section Calculating additional solution fields with n88derivedfields.
You may also note that variables defined on gauss points is a new
category. In essence, this is a higher accuracy version of variables defined
on elements, and it is required for accurately processing
elastoplastic models.
7.4.3. Rendering yielded elements
We can use ParaView to open the solved model file
radius_bending_elastoplastic.n88model. In Figure 33
we’ve rendered the surface of the model such that unyielded elements
are shown in grey, while yielded elements are shown in red. For
elasto-plastic materials, there is a clear distinction between
elements that remain within the elastic limits and therefore have
zero plastic strain, and those
which have exceeded the elastic limits and have non-zero plastic strain.
(where non-zero means that at least one of the 6 components
xx, yy, zz, yz, zx and xy of the plastic strain is non-zero).
In order to generate the rendering of Figure 33 we set the
Coloring to the Magnitude of PlasticStrain. You can find these
in drop-down boxes in the toolbar in ParaView, as shown in
Figure 31. Next we will manually set a tiny
range for the color scale, thus ensuring that practically every element
that is yielded is shown in fully saturated red. If we set a symmetric
scale around zero, then unyielded elements, which have a PlasticStrain
magnitude of zero, will be drawn in a neutral gray. To set the color
scale, click Rescale to Custom Data Range, which is just to
the left of the drop-down box for PlasticStrain, as shown in
Figure 32. For this rendering I used a range of -0.00001 to
0.00001 . Note that in Paraview, the Magnitude of the PlasticStrain
is simply the square root of the sum of the squares of the 6 components
of plastic strain. This quantity has no physical
interpretation, but it is useful for distinguishing yielded and unyielded
elements, as here.

What we observe in Figure 33 rendering is that there are essentially three regions of plastic deformation in this bone subject to a bending force. They are,
-
The uneven head of the bone. This region yields fundamentally because the deformation is applied here, and the surface is rough. Rough surfaces yield easily in localised spots: crudely speaking, you don’t have to push very hard on a pointy little protusion to bend it. This yielding is uninteresting, and if you were to slice the model here, you would find that the yielding is superficial, that is, not very deep.
-
On the inside surface of the bend, the bone yields in compression.
-
On the outside surface of the bend, the bone yields in tension.
You can’t actually tell from Figure 33 what is yielding in compression and what in tension, but with a bit more manipulation, we can generate an image that does show this. Since we know a priori that the tension and compression on the sides of the bone shaft will be predominantly in the z direction, we can change the component of YieldStrain from Magnitude to ZZ. (You may need to manually re-adjust the color scale, as ParaView will automatically rescale to the data range when you change the variable for the color.) Elements yielded in compression now show as blue, as in Figure 34. We have in addition used a Slice filter, as in the previous tutorial. This allows us to see that the yielded region is rather thick.

7.4.4. Numerical results
In comparison with the linear case, the y component of the torque has dropped about 1.5%, from 1.997 N·m to 1.968 N·m; hence a decrease in stiffness of 1.5%. In conclusion, this amount of plasticity has not significantly affected the results.
============================================================================
Table 12: Nodal Torques
----------------------------------------------------------------------------
Torque measured relative to: 60.546 94.150 48.216
----------------------------------------------------------------------------
Node set: 1
Name: face_z1
............................................................................
Tx Ty Tz
total -1.066E+02 -1.967E+03 -3.557E+01
average -3.555E-02 -6.560E-01 -1.186E-02
std_dev 4.106E-01 4.849E-01 7.938E-02
minimum -1.796E+00 -1.831E+00 -2.889E-01
maximum 1.024E+00 1.301E+00 1.671E-01
median -3.379E-02 -6.803E-01 -2.385E-03
----------------------------------------------------------------------------
Node set: 2
Name: face_z0
............................................................................
Tx Ty Tz
total 1.072E+02 1.968E+03 3.570E+01
average 5.497E-03 1.009E-01 1.831E-03
std_dev 2.888E+00 5.542E+00 1.195E+00
minimum -2.380E+01 -2.593E+01 -9.494E+00
maximum 2.158E+01 4.561E+01 1.482E+01
median -1.126E-01 -1.084E+00 1.470E-02
============================================================================
7.4.5. A more careful calculation: incrementally applying the load
There are always more subtle considerations for nonlinear calculations than for linear calculations. One aspect of elasto-plastic calculations is that they exhibit hysteresis, or irreversible changes to strain. In this way, the solutions depend in fact, not only on the current applied state, but in principle on the whole time-dependent history.
Whether this is significant or not in practice is something that can
be investigated experimentally - or rather computationally in our case.
In the present case, we already know that there is only a 1.5% difference
in numerical results
between the linear model and the elastoplastic model. So this
more careful method of applying the load in the nonlinear case is
very unlikely to result in significant differences in the result.
This tutorial is therefore more of a demonstration of principle,
and an introduction to the possibility of modifying already-solved n88model files.
To apply the bending in increments, we will take advantage of the fact
that n88modelgenerator
can accept an existing n88model file as input. In this case, it
will preserve the grid, i.e. the points and elements of the model,
but generate new boundary conditions and/or material definitions.
Crucially, it also preserves an existing solution, which is then
automatically used as the starting value when the solver is
subsequently called.
We are first going to make a configuration file containing all the parameters of n88modegenerator that are the same for each increment of bending.
# File: common.conf # # A configuration file for the tutorial: radius bending with # elast-plastic material properties. # # This file contains all the parameters that don't change on # each increment of bending. test = bending bottom_surface = visible bottom_surface_maximum_depth = 15 plasticity = vonmises,10
Now we are going to call n88modegenerator and faim multiple times, in steps of 0.1º, from bending angle 0.6º up to bending angle 1.0º. 0.6º is chosen as a the starting angle because it happens to be just after the onset of nonlinear behaviour. In general, it takes a bit of experimentation to find the minimum applied test condition for which some elements start to exceed the linear region.
Here are the commands. You may want to put these into a script file.
n88modelgenerator --conf=common.conf --bending_angle=0.6 radius164.aim incremental_bending_0.6.n88model n88solver_spt incremental_bending_0.6.n88model n88modelgenerator --conf=common.conf --bending_angle=0.7 incremental_bending_0.6.n88model incremental_bending_0.7.n88model n88solver_spt incremental_bending_0.7.n88model n88modelgenerator --conf=common.conf --bending_angle=0.8 incremental_bending_0.7.n88model incremental_bending_0.8.n88model n88solver_spt incremental_bending_0.8.n88model n88modelgenerator --conf=common.conf --bending_angle=0.9 incremental_bending_0.8.n88model incremental_bending_0.9.n88model n88solver_spt incremental_bending_0.9.n88model n88modelgenerator --conf=common.conf --bending_angle=1.0 incremental_bending_0.9.n88model incremental_bending_1.0.n88model n88solver_spt incremental_bending_1.0.n88model
Once we have run all of these commands, we can verify that the final
data file, incremental_bending_1.0.n88model, does indeed show the
history of being processed multiple times:
n88modelinfo --history incremental_bending_1.0.n88model
This gives an output of:
History: ---------------------------------------------------------------------- 2016-Sep-27 12:53:47 Model created by n88modelgenerator version 8.0 2016-Sep-27 13:09:03 Solved by n88solver_spt 8.0 2016-Sep-27 13:09:07 Model modified by n88modelgenerator version 8.0 2016-Sep-27 13:21:12 Solved by n88solver_spt 8.0 2016-Sep-27 13:21:16 Model modified by n88modelgenerator version 8.0 2016-Sep-27 13:33:43 Solved by n88solver_spt 8.0 2016-Sep-27 13:33:47 Model modified by n88modelgenerator version 8.0 2016-Sep-27 13:46:27 Solved by n88solver_spt 8.0 2016-Sep-27 13:46:31 Model modified by n88modelgenerator version 8.0 2016-Sep-27 14:03:09 Solved by n88solver_spt 8.0 ----------------------------------------------------------------------
As usual, the details can be recovered with the --log options of
n88modelinfo, but the output is lengthy,
so we will not show it here.
To perform the post-processing on the final result, we call,
n88derivedfields incremental_bending_1.0.n88model n88postfaim incremental_bending_1.0.n88model
Numerically, the results have changed little in this case, as expected. We now have a y-component of torque of 1.972 N·m, which compares with 1.997 N·m in the linear case, and 1.968 N·m for the “all at once” elastoplastic case.
============================================================================
Table 12: Nodal Torques
----------------------------------------------------------------------------
Torque measured relative to: 60.546 94.150 48.216
----------------------------------------------------------------------------
Node set: 1
Name: face_z1
............................................................................
Tx Ty Tz
total -1.116E+02 -1.972E+03 -4.279E+01
average -3.723E-02 -6.579E-01 -1.427E-02
std_dev 4.146E-01 4.921E-01 7.945E-02
minimum -1.818E+00 -1.874E+00 -2.931E-01
maximum 9.960E-01 1.297E+00 1.614E-01
median -4.138E-02 -6.728E-01 -3.365E-03
----------------------------------------------------------------------------
Node set: 2
Name: face_z0
............................................................................
Tx Ty Tz
total 1.116E+02 1.972E+03 4.286E+01
average 5.721E-03 1.011E-01 2.197E-03
std_dev 3.191E+00 6.173E+00 1.345E+00
minimum -2.732E+01 -2.842E+01 -1.075E+01
maximum 2.276E+01 4.839E+01 1.579E+01
median -1.405E-01 -1.222E+00 2.123E-02
============================================================================
This tutorial is the final tutorial in the series presenting the Faim standard workflow,
with models generated by n88modelgenerator. Those
interested in generating custom models will want to continue on to the
tutorials presenting vtkbone. If you intend for the moment to use only
n88modelgenerator for generating your models, then
you can stop here.
7.5. Tutorial: Compressing a cube revisited using vtkbone
In the preceding tutorials, we used n88modelgenerator
to quickly generate finite element models from segmented 3D images.
n88modelgenerator has many parameters that can
be used to tune the models in produces, but inevitably, the variety of
models that can be produced using the parameter-setting approach is limited.
A far more flexible approach is scripting. Numerics88 contains a collection
of objects suitable for constructing
and manipulating finite element objects. These can be scripted with Python.
Python is one of the easiest languages
to learn, and yet retains a great deal of expressive power. This
collection of objects is built on top of VTK and is referred
to as vtkbone. It is documented in Preparing Finite Element Models with vtkbone.
In this tutorial, we are going to revisit the first tutorial,
Introductory tutorial: Compressing a solid cube.
In fact we’re going to do it all over again, only this time, we will
generate the model by writing a little script with vtkbone, instead
of using n88modelgenerator. It will be
more work, but we will have a working model-generation script that could
be further tweaked to do things that would not be possible with
n88modelgenerator.
7.5.1. Getting familiar with Python, VTK and Numpy
It is not necessary to know Python in order to write and
modify scripts using vtkbone, as very often you can make obvious
modifications to existing scripts. However, having a basic familiarity
can make you more comfortable with the following scripting. As
Python is very widely used, there are any number of excellent
introductory books. A suggested place to start is the on-line
tutorial at http://docs.python.org/tutorial/ .
One feature of Python which we will use that is not a part of the standard Python distribution (but is distributed with Numerics88 software) is Numpy, which efficiently handles numerical arrays in Python. Again, prior knowledge of Numpy is not required, but will help. Documentation for Numpy can be found at http://docs.scipy.org/doc/ . We recommend https://docs.scipy.org/doc/numpy-dev/user/quickstart.html as an introduction.
Finally, there is VTK . VTK is quite complex and rather
more difficult to learn than either Python or Numpy, but fortunately it
is not necessary to know very much VTK. We will be using
a mixture of custom vtkbone objects and standard VTK objects. When one
of these comes up in the following tutorials, you may want to
have a glance at the corresponding API documentation for that object.
This is explained in vtkbone API documentation.
7.5.2. Preliminaries: first lines of Python
First create a working directory. Using your favourite text editor, create a
file apply_compression.py.
|
|
You can also use an editor or an integrated development environment specifically intended for python, such as IDLE, but this is not necessary. A plain old text editor will work fine. On Windows, Notepad can be used. On OS X, you can use TextEdit, which you will find in the Utilities folder within Applications. If using TextEdit, be sure to select . Atom is an open-source text editor with a variety of tools for scripting in Python. |
|
|
If you want to cheat and not actually type this tutorial script
line-by-line as we go, you can find the finished version in the
directory tutorials/cube_with_vtk, once you unpack the archive
of tutorial data that can be downloaded from http://numerics88.com/downloads .
|
Start by adding these lines, which import all the Python modules that we will be using:
from __future__ import division import argparse import os import sys import vtk import vtkbone
Once you save this, you already have a script that you can run! In fact, you should run it,
with just these lines
in it - even though it does nothing yet, because it will verify that Python can
successfully locate VTK and vtkbone. The script can be run like this
(make sure you’ve saved apply_compression.py),
$ python apply_compression.py
|
|
The dollar sign ($) at the beginning of the line is the prompt:
don’t type that. On Windows the prompt will be something like C:\> .
On all systems the prompt might contain additional information, such
as the current directory.
|
You should get as output . . . nothing whatsoever. If you get an error like “ImportError: No module named vtk”, then it is likely that the n88tools is not installed, or that the anaconda python environment is not activated. Refer to Install n88tools and vtkbone.
We recommend also having a version number in your script. Increment it
whenever you change the script (not every time you
add a line, but if you modify the finished script later so that the
resulting model is somewhat different, then increment the version number.)
We’ll see soon how we can
ensure that the script version number gets written into the log
of the n88model file. Although we’re not accountants, we highly
recommend having an audit trail that will allow you to know exactly how
a given model was generated. (Obviously, you should archive copies of every
version of your script, not just the most recent one. You should also
floss daily, which we’re sure that you do.) For now, just add a version
number to the script with this line. We are on version 3, since
this tutorial has been in the manual for quite some time, and it has been
tweaked a couple of times.
script_version = 4
Now, we’re going to want to specify the input image file on the
command line, because this will allow us to use the script on
any input file, not just one hard-coded by name into the script.
We’re also going to want to inform the user that an input
file name is required if they don’t supply one. (“The user” is most likely
you yourself, but don’t assume that next week you’ll remember how you
intended to use the script you write this week.) The python module
argparse is really handy for this. The following lines will do
the desired thing:
parser = argparse.ArgumentParser (
description="""Apply a compression test.
This script does essentially the same as the command
"n88modelgenerator --test=uniaxial"
but uses vtkbone for this purpose.
""")
parser.add_argument ("input_file",
help="An input image file of the segmented data; must be in VTK XML format (.vti).")
args = parser.parse_args()
So now when we run it as before, this time we do get some output:
$ python apply_compression.py usage: apply_compression.py [-h] input_file apply_compression.py: error: too few arguments
Progress!
Let’s see what happens if we run it with the -h flag. Note that argparse has
automatically added a -h flag, the purpose of which is to get help about the
command.
$ python apply_compression.py -h
usage: apply_compression.py [-h] input_file
Apply a compression test. This script does essentially the same as the command
"n88modelgenerator --test=uniaxial" but uses vtkbone for this purpose.
positional arguments:
input_file An input image file of the segmented data; must be in VTK XML
format (.vti).
optional arguments:
-h, --help show this help message and exit
7.5.3. Reading the input file
The input file is cube6x6x6.vti and as usual you can find it in the
data folder of your distribution. We’ve seen it before in the
first tutorial. Copy it to your working directory.
As the data is in VTK’s .vti format (properly referred to as
“VTK XML Image Data file format”), we’ll need a vtkXMLImageDataReader
object to read it. That will look like this:
print(f"Reading, {args.input_file}")
reader = vtk.vtkXMLImageDataReader()
reader.SetFileName(args.input_file)
reader.Update()
image = reader.GetOutput()
vtkXMLImageDataReader is a type of VTK “filter” (specifically a “source”). What we’ve done is very typical for VTK filters and we’ll see this sequence of steps for employing a VTK filter over and over again. It is,
-
Create the filter object.
-
Set any inputs. (Here there are none, because a source doesn’t have any.)
-
Set any parameter values. In this case we set the parameter value
FileName(). -
Call
Update(). (Otherwise nothing happens and we wonder why.) -
Get any output.
In fact, this isn’t the only way to use VTK filter objects, but it is the simplest and it is the procedure we will nearly always employ in our scripts.
Let’s provide some feedback at this point so we have some indication that the data was correctly read. While we’re at it, let’s do some error checking to stop things right here if that data wasn’t able to be read,
if not image:
print("No image data read.")
sys.exit(1)
print(f"Read image with point dimensions: {image.GetDimensions()}")
Now running it should result in,
$ python apply_compression.py cube6x6x6.vti Reading cube6x6x6.vti Read image with point dimensions (7, 7, 7)
| Wait a minute! Why are the reported dimensions (7, 7, 7) when they are really 6×6×6? It is because these are the reported Point (or Node) dimensions, rather than the Cell (or Element) dimensions. If you’re confused, review the discussion on this point in Introductory tutorial: Compressing a solid cube. |
7.5.4. Ensuring connectivity
We could assume that the input image is properly segmented and just proceed with generating a mesh. Since this is an introductory tutorial perhaps we should. However, it happens not infrequently for whatever reason that a finite element model is attempted on an image which does not consist of a single connected object. This can cause all sorts of trouble. Consider this: if there are disconnected floating bits in the model, where is the proper place for the solver to put them in the solution? Sometimes the solution of such models will be very slow, other times the model will solve OK, but some of the post-processing numbers may appear strange if you don’t realize that they are calculated over the entire model, including bits which are subject to no constraints.
So to avoid potential grief, this is a good place to drop in a vtkboneImageConnectivityFilter . It will strip away (actually zero-out) any parts of the input image that aren’t in some way connected to the largest object in the image. It is a safe and prudent step in the generation of a well-defined finite element model.
print("Applying connectivity filter.")
connectivity_filter = vtkbone.vtkboneImageConnectivityFilter()
connectivity_filter.SetExtractionModeToLargestRegion()
connectivity_filter.SetInputData(image)
connectivity_filter.Update();
image = connectivity_filter.GetOutput()
|
|
Is it legitimate to assign the output to the variable image when that was also the name of the input? The answer is yes. It’s quite kosher in Python to clobber a variable name by assigning it to something else. Python is more clever than you might think about this. It will in fact keep the data associated with the original input variable around as long required, even though we have no means to refer to it or access it now. (And technically speaking, here it will be required, at least as long as connectivity_filter exists, because connectivity_filter will still use the original input data. As long as connectivity_filter is around, we might decide to use it again without changing the input, so Python won’t get rid of it.) |
7.5.5. Generating a mesh
The filter object for generating an FE mesh from an input image is vtkboneImageToMesh . The FE mesh represents the geometry of the model, and consists of elements and nodes (concretely, it will be an object of type vtkUnstructuredGrid ). Note that in VTK terminology, elements will be called Cells, and nodes will be called Points. Most of the time we don’t need to set any parameters to vtkboneImageToMesh except the input.
# Generate a finite element mesh from the input image
geometry_generator = vtkbone.vtkboneImageToMesh()
geometry_generator.SetInputData(image)
geometry_generator.Update()
geometry = geometry_generator.GetOutput()
print(f"Generated {geometry.GetNumberOfCells()} elements and {geometry.GetNumberOfPoints()} nodes.")
Now our output is beginning to get interesting,
$ python apply_compression.py cube6x6x6.vti Reading cube6x6x6.vti Read image with point dimensions (7, 7, 7) Applying connectivity filter. Generated 216 elements and 343 nodes.
Quick check: 63 = 216 and 73 = 343, so we’re good.
|
|
It is possible to write out the geometry to a file in VTK’s XML Unstructured Grid format using vtkXMLUnstructuredGridWriter . You will then be able to open it in ParaView. It should be very similar to Figure 16. (In contrast though to rendering the input image, if there were any zero-valued voxels, there would be no need to threshold to remove the corresponding cells, as they are already absent from the meshed geometry.) The lines of code to save the geometry to a file are as follows: writer = vtk.vtkXMLUnstructuredGridWriter()
geometry_file = "geometry.vtu"
print(f"Writing geometry to {geometry_file}")
writer.SetFileName(geometry_file)
writer.SetInputData(geometry)
writer.Write()
|
7.5.6. Defining materials and creating a material table
Now we need to define some material properties. We can do this by creating an instance of some specific derived class of vtkboneMaterial . The one of these is vtkboneLinearIsotropicMaterial . Let’s make one of them,
print("Creating a linear isotropic material.")
material = vtkbone.vtkboneLinearIsotropicMaterial()
material.SetName("linear_iso_material")  material.SetYoungsModulus(6829)
material.SetYoungsModulus(6829)  material.SetPoissonsRatio(0.3)
material.SetPoissonsRatio(0.3) 
| We can give it any name we want. If we need to access it later, we can look it up by name. | |
| These are default values, so we actually didn’t really need these lines, but it doesn’t hurt be explicit, and now it is clear how to set different values should you want to do so. |
The other thing we must do is to make a material table, which associates
the values in the input image (segmentation IDs or material IDs)
with defined materials. Our image file cube6x6x6.vti has the uniform
value of 1 on every voxel, so we need to make a material table that
associates 1 with our material defined above. But perhaps we
might want to run this script someday on an input file that uses different
values (127 is very common for historical reasons). We could write
here some fancy scripting that would examine the input data and produce a
list of all the different values in the image, then map all those values
to our material (since we’re only using one material here). This
sounds a bit complicated, but fortunately, there is a vtkbone object,
vtkboneGenerateHomogeneousMaterialTable , that
does exactly this for us:
mt_generator = vtkbone.vtkboneGenerateHomogeneousMaterialTable() mt_generator.SetMaterial(material) mt_generator.SetMaterialIdList(image.GetCellData().GetScalars())mt_generator.Update() material_table = mt_generator.GetOutput() print(f"Generated material table with {material_table.GetNumberOfMaterials()} entries.")
Unfortunately, it is not as simple as just setting “image” as
the argument to SetMaterialIdList. We have to be quite explicit about specifying the
scalar data on the cells, in this manner. |
7.5.7. Applying a compression test
To apply boundary conditions appropriate to a compression test, we can make use of the object vtkboneApplyCompressionTest , which will do practically all the work for us. vtkboneApplyCompressionTest requires as inputs both the mesh and the material table that we defined above.
# Apply a compression test (uniaxial)
print("Applying a uniaxial compression test.")
generator = vtkbone.vtkboneApplyCompressionTest()
generator.SetInputData(0, geometry)  generator.SetInputData(1, material_table)
generator.SetInputData(1, material_table) 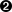 generator.Update()
model = generator.GetOutput()
generator.Update()
model = generator.GetOutput()
| Input 0 to vtkboneApplyCompressionTest must be the mesh geometry, as a vtkUnstructuredGrid object. | |
| Input 1 to vtkboneApplyCompressionTest must be the material table, as a vtkboneMaterialTable object. |
7.5.8. Writing an n88model file
The output of vtkboneApplyCompressionTest is a vtkboneFiniteElementModel
object, which is a complete representation of the problem we want to
solve with finite element analysis. It remains to write out this model
in n88model file format.
# Write an n88model file output_file = os.path.splitext(args.input_file)[0] + "_custom.n88model"# Remove directory, so file ends up in current directory. output_file = os.path.split(output_file)[1] print(f"Writing n88model file: {output_file}") writer = vtkbone.vtkboneN88ModelWriter() writer.SetInputData(model) writer.SetFileName(output_file) writer.Update()
| This is some fancy Python to derive the output file name from the input file name. |
That’s it. If everything works correctly, the output should look like this:
$ python apply_compression.py cube6x6x6.vti Reading cube6x6x6.vti Read image with point dimensions (7, 7, 7) Applying connectivity filter. Generated 216 elements and 343 nodes. Creating a linear isotropic material. Generated material table with 1 entries. Applying a uniaxial compression test. Writing n88model file: cube6x6x6_custom.n88model
7.5.9. Modifying the file history and log
We promised at the beginning to record the script version number in the file, and so far we haven’t done this. First we’ll have a look at what is currently in the history field.
$ n88modelinfo --history cube6x6x6_custom.n88model History: ---------------------------------------------------------------------- 2012-Sep-24 08:18:01 Model created by vtkboneApplyCompressionTest version 1.0 . ----------------------------------------------------------------------
This is useful information so instead of replacing it, we can just add to it. To do this, add the following line to the script, just before writing out the file:
model.AppendHistory(f"Created by cube_compression.py version {script_version}.")
Now run the script again, and this time when we run n88modelinfo, we get:
$ n88modelinfo --history cube6x6x6_custom.n88model History: ---------------------------------------------------------------------- 2012-Sep-24 08:22:14 Model created by vtkboneApplyCompressionTest version 6.0 . 2012-Sep-24 08:22:14 Created by apply_compression.py version 2 . ----------------------------------------------------------------------
Good, now we’ll always know that the cube6x6x6_custom.n88model file was
created with version 2 of the script (which called vtkboneApplyCompressionTest from vtkbone version 6.0).
We can also have a look at the log, which gives more detailed information:
$ n88modelinfo --log cube6x6x6_custom.n88model Log: ---------------------------------------------------------------------- 2012-Sep-24 08:22:14 vtkboneApplyCompressionTest settings: TopConstraintSpecificMaterial: -1 BottomConstraintSpecificMaterial: -1 UnevenTopSurface: 0 UnevenBottomSurface: 0 TestAxis: 2 AppliedStrain: -0.01 AppliedDisplacement: 0 TopSurfaceContactFriction: 0 BottomSurfaceContactFriction: 0 ConfineSides: 0 Pin: 0 PinCellClosestToXYCenter: 1 PinCellId: 0 ----------------------------------------------------------------------
There is already quite a lot of information here, provided automatically
by vtkboneApplyCompressionTest . In particular we have all the
parameters of vtkboneApplyCompressionTest , which were all set to
default values because we didn’t change any of them.
We could, if we wanted, add even more information to the log, using the method
model.AppendLog, just as we used model.AppendHistory. In this case, there is
nothing lacking that we can’t query. For example, although no
material information appears in the log, we can determine it
with n88modelinfo,
$ n88modelinfo --materials cube6x6x6_custom.n88model Materials: ---------------------------------------------------------------------- Name : linear_iso_material Type : LinearIsotropic E : 6829.0 nu : 0.3 ----------------------------------------------------------------------
You can now proceed if you want to solve and analyze the model exactly as in An introductory tutorial: compressing a solid cube.
This completes the tutorial on building the 6×6×6 cube
compression model using vtkbone. We’ve seen that it takes considerably
more work to write a script than to call n88modelgenerator,
so whenever it suffices,
it is preferable to use n88modelgenerator. However,
although in this case we’ve done nothing that n88modelgenerator
couldn’t have done, we hope that you can imagine that now that we have
a script, that we could potentially modify it in any number of ways beyond
what would be possible with n88modelgenerator.
In subsequent tutorials, we’ll explore these possibilities.
7.6. Tutorial: Deflection of a cantilevered beam; adding custom boundary conditions and loads
In this tutorial, we are going to use vtkbone to create a model that is
different than anything that could create with n88modelgenerator.
The test will be the deflection
of a uniform beam fixed at one end, in other words a cantilever. We have chosen this model
because there is a simple analytic solution to which we can compare the result.
One aspect that will be new to this tutorial will be an applied force as part of the problem definition. Generally though, it is preferable to define models with fixed position boundary conditions and solve for the forces, rather than to specify forces and solve for a displacement. The reason for this will be discussed in the subsequent tutorial.
The completed script, create_cantilever.py, can be found in the cantilever subdirectory
in the examples.
7.6.1. Importing the required python modules
As in the previous tutorial, we start the python script by importing
the python modules that we will need. This time we will also need the
numpy module, as we are going to do some array manipulation.
from __future__ import division import argparse import numpy from numpy.core import *import vtk import vtkbone from vtk.util.numpy_support import vtk_to_numpy, numpy_to_vtk
This just saves some typing later. For example we’ll be able to use the function
array instead of the longer numpy.array. |
|
| These are the functions that allow us to convert numpy arrays to and from VTK data arrays. |
As before, we’ll also set a script version number:
script_version = 3
7.6.2. Setting command line options
As before, we use the argparse module, which makes it quite simple to
define a couple of arguments for running the script, one of which,
the applied force, will have a numerical value.
parser = argparse.ArgumentParser (
description="""Generate a model for a cantilever with an
applied force to the end of the beam.""")
parser.add_argument ("applied_force", type=float,
help="The applied force to the end of the beam.")
parser.add_argument ("output_file",
help="Name for output n88model file.")
args = parser.parse_args()
7.6.3. Generating the image data
The beam is going to have a very simple geometry, one which we generate algorithmically without too much trouble. This is also going to serve as a brief introduction to numpy arrays. Because the analytic solution for the cantilever is essentially a 2D problem, we are going to use just a beam width of just a single element. To scale up to a realistic width, if desired, one can just scale all the forces. We are going to create a beam of 200×1×20 elements, with a cubic element of side length 0.5mm. Thus the beam has dimensions of length 100mm, height 10mm, and width 0.5mm (but again, everything scales linearly with the width, so the obtained solution can be used for arbitrary widths).
Here is how we create a 3-dimensional array data of size 200×1×20:
dims = array ((20, 1, 200))cellmap = ones (dims)
| The order of the dimensions is z,y,x, because numpy indices always are ordered with the “fastest-changing” index last, which must be x. On the other hand, VTK will generally want arguments specified as x,y,z. We will have to be careful about which order to use when. | |
ones is a numpy function that creates an array (in this case a
3-dimensional array) filled with 1s. |
We need to convert this from a numpy array, which is natural to Python, to
a VTK data array:
cellmap_vtk = numpy_to_vtk(ravel(cellmap), deep=1, array_type=vtk.VTK_INT)
There are a couple of subtle points here. The first is that VTK is actually
going to want the flattened data, meaning as one long 1-dimensional
array, rather than as a 3-dimensional array. (It will keep track of the
dimensionality separately, as we will see below.) Hence the use of ravel
function, which is a numpy function that returns the input array as a
one-dimensional array (without copying the underlying data if possible).
The other aspect to note is that we specify deep=1, which specifies
that the VTK array should create its own copy of the underlying
data, instead of just referring to the numpy data. This is less memory
efficient, but there are potential pitfalls with sharing the data, so we’ll
go with the more robust method of making a copy.
Now that we have the data, we’re going to create a vtkImageData object which adds information such as the dimensions and the spacing.
image = vtk.vtkImageData() image.SetDimensions(dims[::-1] + 1)image.SetSpacing(0.5, 0.5, 0.5) image.GetCellData().SetScalars(cellmap_vtk)
This is a little bit tricky. First, dims[::-1] simply means
“dims reversed”, which we need because, as discussed above, dims
is ordered z,y,x, but VTK requires x,y,z. Secondly we’re
adding 1 (to every dimension) because vtkImageData dimensions
are always in terms of the number of Points, rather than the number
of Cells. The end result is (201, 2, 21). |
We’ve set the spacing to 0.5 . In this tutorial, we are going to use
units of millimetres. Units are not specified in the
n88model file. Instead we will just have to ensure
that all our units are consistent.
See A note about units.
We can at this point write out the vtkImageData as a .vti file,
and open it with ParaView to ensure that we have obtained the desired result.
It should ressemble Figure 35. As a beam, it looks absurdly thin, but
to emphasise once again, we are solving essentially a 2D problem; the
numerical results obtained can be scaled to any beam width.
# Optional: write out image data to examine it
print("Writing geometry file: beam_image.vti")
writer = vtk.vtkXMLImageDataWriter()
writer.SetInputData(image)
writer.SetFileName("beam_image.vti")
writer.Update()

7.6.4. Generating a base model without boundary conditions
Now that we have an image, as in the previous tutorial, we convert it to a geometric mesh:
# Generate a geometrical mesh from the input image mesh_generator = vtkbone.vtkboneImageToMesh() mesh_generator.SetInputData(image) mesh_generator.Update() mesh = mesh_generator.GetOutput()
We also define a material (steel) and a material table.
# Create a material
material = vtkbone.vtkboneLinearIsotropicMaterial()
material.SetName("steel")
material.SetYoungsModulus(2.0E5)  material.SetPoissonsRatio(0.3)
material_table = vtkbone.vtkboneMaterialTable()
material_table.AddMaterial (1, material)
material.SetPoissonsRatio(0.3)
material_table = vtkbone.vtkboneMaterialTable()
material_table.AddMaterial (1, material) 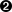
| 200GPa is a typical value for the Young’s modulus of steel. We will use units of MPa. We have already declared that our length units are mm, hence all units will be consistent provided that we use Newtons for forces. | |
| The value 1 comes from the fact that we filled our image with 1s. All the elements will now be mapped to the material steel. |
In contrast to the previous tutorial, we won’t be using one of the standard test generation filters. Rather we will use the base test generation filter vtkboneApplyTestBase , which creates a vtkboneFiniteElementModel object without any boundary conditions.
# Create a model without boundary conditions. generator = vtkbone.vtkboneApplyTestBase() generator.SetInputData(0, mesh) generator.SetInputData(1, material_table) generator.Update() model = generator.GetOutput()
Before we add displacement boundary conditions and applied loads, let’s save the model so we can examine the results as we build up our script. Of course the model isn’t complete yet, but that doesn’t prevent us from saving and examining it.
# Write an n88model file
print(f"Writing n88model file: {args.output_file}")
writer = vtkbone.vtkboneN88ModelWriter()
writer.SetInputData(model)
writer.SetFileName(args.output_file)
writer.Update()
|
|
In everything that follows, it is intended that you add new lines to the script before the code (shown just above) that saves the model to a file. Otherwise of course the saved file won’t include our additions and changes. |
To run the script will require both a numerical value for the applied force and an output file name. For now use these values:
python create_cantilever.py -10 cantilever.n88model
We are choosing to use a negative applied force, because it is more natural to think of a downward force applied to a cantilever.
7.6.5. Adding fixed boundary conditions
We want to fix one end of our beam, to weld it to the (virtual) wall. Usually the step requiring the most work in defining boundary condition is identifying the set of nodes that constitute the boundary surface we are interested in. In this case, vtkboneApplyTestBase has done the work for us, because although it doesn’t define any boundary conditions, it does define node (and element) sets on all the faces. (To be more precise, it defines node and element sets consisting of any nodes/elements located at the x,y and z extents of the model.) This is discussed in Creating node and element sets. The names of these sets are listed there, but if you’ve run the script up to this point, you can also use n88modelinfo to query the set names:
$ n88modelinfo --node_sets cantilever.n88model NodeSets: ---------------------------------------------------------------------- Name : face_z0 Part : Part1 NumberOfNodes : 402 Name : face_z1 Part : Part1 NumberOfNodes : 402 Name : face_x0 Part : Part1 NumberOfNodes : 42 Name : face_x1 Part : Part1 NumberOfNodes : 42 Name : face_y0 Part : Part1 NumberOfNodes : 4221 Name : face_y1 Part : Part1 NumberOfNodes : 4221 ----------------------------------------------------------------------
There are also corresponding element sets, which can be listed with
the --element_sets option to n88modelinfo.
Node set face_x0 is the one to which we are interested in applying a fixed
boundary condition. If you refer
to the the API documentation for vtkboneFiniteElementModel, you
will see that there are a number of methods for defining boundary
conditions. One possibility is to use the method FixNodes, which
will fix the specified node set in all senses (directions). Only
one line of code would be required:
model.FixNodes ("face_x0", "fixed_beam_base") 
| face_x0 is the name of an existing node set; fixed_beam_base is the name we are assigning to the new constraint. |
However, as we are trying to obtain a result as close as possible to the
analytic 2D solution, it is actually better to not limit the freedom of
motion in the y direction on the boundary condition. This way, no
y direction forces will arise. Were there to be any forces in the y
direction, this would cause some essentially 3D effect on the x-z plane
by the mechanism of Poisson’s ratio. So instead of using FixNodes,
we will use the following slightly more verbose code
# Create the fixed boundary conditions at the base of the beam.
# To obtain a more truely 2D result, no constraint is applied to
# displacements in the _y_ direction.
model.ApplyBoundaryCondition(
"face_x0",
vtkbone.vtkboneConstraint.SENSE_X,
0,
"fixed_beam_base_x")
model.ApplyBoundaryCondition(
"face_x0",
vtkbone.vtkboneConstraint.SENSE_Z,
0,
"fixed_beam_base_z")
If you now run the script, you can then use n88modelinfo to verify that the boundary condition has indeed been generated:
$ n88modelinfo --constraints cantilever.n88model Constraints: ---------------------------------------------------------------------- Name : fixed_beam_base_x Part : Part1 Type : NodeAxisDisplacement NumberOfValues : 42 Name : fixed_beam_base_z Part : Part1 Type : NodeAxisDisplacement NumberOfValues : 42 ----------------------------------------------------------------------
7.6.6. Adding an applied load to tip of the beam
At the free end of the beam, we are going to apply a load. Creating an applied load is very similar to creating a displacement boundary condition. vtkboneFiniteElementModel provides a number of methods for this purpose. There are some important differences,
-
Applied loads are applied to element sets; displacement boundary conditions are applied to node sets.
-
Applied loads require the additional specification of a particular face of the elements to which to apply the load, or else the specification that it is a body force. We are going to apply the load to the outward faces of the end elements (i.e. those facing in the x direction).
Here is the code to create an applied load constraint, named end_force to the pre-defined element set face_x1. corresponding to the end face of the beam.
# Apply a force to the far end of the beam model.ApplyLoad( "face_x1",vtkbone.vtkboneConstraint.FACE_X1_DISTRIBUTION,
vtkbone.vtkboneConstraint.SENSE_Z,
args.applied_force,
"end_force")
| This node set was created by vtkboneApplyTestBase . Here face_x1 means elements on the x1 face of the entire model. | |
| This specifies the x1 faces of the elements. | |
This specifies the direction of the applied force. (The value of
vtkbone.vtkboneConstraint.SENSE_Z is 2, but the named constant conveys
the intent more clearly than the numerical value.) |
|
| The applied force will be equally divided among the element faces in the set. Units, as discusssed above, are Newtons. | |
| The name of the newly-created constraint. |
7.6.7. Adding a convergence set
As discussed in Convergence measure there are different possibilites for the convergence measure, which is used by the solver to determine when the solution has iterated enough to obtain an acceptable solution. Generally, the best convergence measure to use for linear problems is convergence set. This convergence measure can only be used if we define a convergence set within the model file. A convergence set is something that we choose, and we generally want to choose the quantity that we are most interested in calculating. For example, for a cantilever, this quantity could be the displacement of the tip of the cantilever. You might imagine that this would be difficult to specify. But in most cases, this quantity of interest is the complement of some boundary condition or applied force. In this case, the displacement is the complement of the force applied to the tip. There is a method to generate a convergence set from a boundary condition or from an applied force, and it is very simple to use:
# Create a convergence set: the displacement of the tip
model.ConvergenceSetFromConstraint("end_force")
This method notices that the constraint named end_force, which we created previously, is an applied force, and that it is applied to the faces of certain elements. It then constructs the compliment, which is the displacement, averaged over all nodes located on those element faces. It is this average displacement of the tip that the solver will watch to determine when its value ceases to change meaningfully. At that point the solver is finished.
|
|
In this case we have passed an applied force to |
|
|
The fact the we define a convergence set in the model file does not limit us to choosing the convergence set convergence measure. Although the solver will default to using the convergence set convergence measure if it finds a convergence set defined in the n88model file, we can always run the solver while specifying a different convergence measure, using the option convergence_measure. Similarly, we can skip altogether defining a convergence set, and the solver will default to a convergence measure that doesn’t require it. The only drawback is that the other convergence measures are necessarily more conservative, and so the solver will usually run for more iterations than would be strictly necessary for the desired precision. |
7.6.8. Specifying sets for post-processing
There is one more step required, and that is to identify the sets to be used for post-processing calculations by n88postfaim. We are interested in values on the sets face_x0 and face_x1. The magic lines of code are:
# Set the node sets and element sets that will be used for post-processing info = model.GetInformation() pp_node_sets_key = vtkbone.vtkboneSolverParameters.POST_PROCESSING_NODE_SETS() pp_elem_sets_key = vtkbone.vtkboneSolverParameters.POST_PROCESSING_ELEMENT_SETS() pp_node_sets_key.Append(info, "face_x0") pp_elem_sets_key.Append(info, "face_x0") pp_node_sets_key.Append(info, "face_x1") pp_elem_sets_key.Append(info, "face_x1")
After running the script, we can verify that these post-processing sets
are in fact specified in the n88model file:
$ n88modelinfo --problems cantilever.n88model Problems: ---------------------------------------------------------------------- Name : Problem1 Part : Part1 Constraints : fixed_beam_base_x,fixed_beam_base_z,end_force ConvergenceSet : convergence_set PostProcessingNodeSets : face_x0,face_x1 PostProcessingElementSets : face_x0,face_x1 ----------------------------------------------------------------------
|
|
It is possible to skip this step, and instead to specify later the node and element sets to be used by n88postfaim on the command line of n88postfaim with the argument --sets=face_x0,face_x1 |
7.6.9. Documenting the model in the file log
As discussed previously, it is good practice to document the model creation in both the file History and the file Log. Here we add these lines (again they must come before the code that saves the model):
# Update history and log
model.AppendHistory(f"Created by create_cantilever.py version {script_version} .")
model.AppendLog(
f"""create_cantilever.py
Cantilever beam model with applied force on far face edge of {args.applied_force} .
Using vtkbone version {vtkbone.vtkboneVersion.GetvtkboneVersion()} .
"""
)
If we run the script to generate the n88model file, we can at
any later time get a brief description of the model and determine
what versions were used (including what version of vtkbone).
$ n88modelinfo --history --log cantilever.n88model History: ---------------------------------------------------------------------- 2016-Sep-22 17:33:32 Created by create_cantilever.py version 3 . ---------------------------------------------------------------------- Log: ---------------------------------------------------------------------- 2016-Sep-22 17:33:32 create_cantilever.py Cantilever beam model with applied force on far face edge of -10.0 . Using vtkbone version 1.0 . ----------------------------------------------------------------------
7.6.10. Solving the problem and comparing with theory
The model is quickly solved with faim:
$ faim cantilever.n88model
If we open the solved file cantilever.n88model in ParaView, we can
observe the beam deflection as shown in Figure 36.
Here the deflection is amplified by 10 so as to be more evident.
The figure is colored by the xx component of strain, with red being
tensile and blue being compressive. This is easily done in ParaView, simply
by selecting the relevant quantities from the drop-down boxes in the toolbar,
as in Figure 37.


Now let’s compare quantitatively with the analytical result for deflection of a cantilever beam as found in any Mechanics of Solids textbook or on wikipedia at https://en.wikipedia.org/wiki/Deflection_%28engineering%29. We have that the deflection δ of the end of a cantilever beam is
where
| \(F\) |
= force acting on the tip of the beam |
| \(L\) |
= length of the beam (span) |
| \(E\) |
= modulus of elasticity |
| \(I\) |
= area moment of inertia |
For a beam with a rectangular cross-section \(b \times h\), the area moment of inertia is
so that we have
You can observe this deflection in ParaView, and we can get a
precise number by looking in the beam_analysis.txt file, in the table
Nodal Displacements. In this case
the result, 0.4018, is very close to 0.4 .
This concludes the cantilever beam tutorial. We learned how to create
custom models using vtkbone that are beyond the standard types of models
that n88modelgenerator can generate. We were also
introduced to a new type of constraint, which was the applied load.
7.7. Tutorial: A cantilevered beam with elastoplastic material properties
This tutorial uses the same model as the previous one, but now we will solve it using nonlinear elastoplastic material properties.
7.7.1. Analytic solution
The cantilever problem has a known analytic solution even in the case of nonlinear elastoplastic material properties. This solution is due to Timoshenko and Gere (1997).
Before building and solving some models, we will consider the analytic solution, because it will indicate what range of test loads are both interesting and reasonable, which is a non-trivial question for nonlinear problems.
The applied load at which the cantilever begins to yield, Fy, is
where σy is the material yield strength (i.e. the value of uniaxial stress at which the material starts to yield), and all other symbols are as in the previous section.
For our current model, for which we will use σy = 120 MPa, this evaluates to
You will notice that this value corresponds (not entirely coincidently) with the applied force used for the linear case in the previous section, for which we had calculated a deflection of 0.4 mm.
In the yielding region, the beam deflection is
This expression is only valid for 1 ≤ F / Fy ≤ 3/2; the cantilever will not withstand any force larger than this. For the current model this range corresponds to between 10 N and 15 N.
7.7.2. Changes to the generation script
The model generation script is named create_cantilever_ep.py. It differs from the script in the
previous tutorial, create_cantilever.py, only in the definition of the
material. This becomes
# Create a material
material = vtkbone.vtkboneVonMisesIsotropicMaterial()
material.SetName("steel")
material.SetYoungsModulus(2.0E5) # units are MPa
material.SetPoissonsRatio(0.3)
material.SetYieldStrength(120) # units are MPa
For a von Mises elastoplastic material, we have exactly one new parameter
as compared with a linear material, and that is the yield strength, here
set to 120 MPa. The exact parameters required depend on the material. For
example a Mohr Coulomb material would have two additional parameters,
which are set with the method SetYieldStrengths(Y_tension,Y_compression).
As always, for exact usage refer to the vtkbone API documentation
( vtkboneVonMisesIsotropicMaterial and
vtkboneMohrCoulombIsotropicMaterial ).
7.7.3. Generating the model and verifying the material
As in the linear case, we generate the model with
python create_cantilever_ep.py -14.5 cantilever_ep_145.n88model
And we can quickly verify that this model uses a von Mises material with
n88modelinfo --material cantilever_ep.n88model
The output is
Materials: ---------------------------------------------------------------------- Name : steel Type : VonMisesIsotropic E : 200000.0 nu : 0.3 Y : 120.0 ----------------------------------------------------------------------
7.7.4. Solving the model
The cantilever is, for various reasons, a particularly difficult model for a finite element solver. When combined with nonlinear material properties, in order to get the most accurate results, it is necessary to tighten the convergence tolerance. Thus for the following results, we ran the solver as follows,
faim --convergence_tolerance=1E-9 cantilever_ep_145.n88model
|
|
Although this is a small model, elastoplastic models take considerably
longer to run than linear models, so if you have a system with a suitable
GPU, make use of the option |
7.7.5. Plastic strain distribution
A solution with applied force of 14.5 N is shown in Figure 39. In comparison with the linear case of Figure 36, we see that the strain is much more concentrated near the fixed end of the beam.
7.7.6. Comparison of finite element and analytic results
By generating and solving models for various loads in the plastic range, we can generate table Elastoplastic cantilever results. To do this, first we create a number of sequence of models
python create_cantilever_ep.py -10.0 cantilever_ep_100.n88model python create_cantilever_ep.py -10.5 cantilever_ep_105.n88model python create_cantilever_ep.py -11.0 cantilever_ep_110.n88model python create_cantilever_ep.py -11.5 cantilever_ep_115.n88model python create_cantilever_ep.py -12.0 cantilever_ep_120.n88model python create_cantilever_ep.py -12.5 cantilever_ep_125.n88model python create_cantilever_ep.py -13.0 cantilever_ep_130.n88model python create_cantilever_ep.py -13.5 cantilever_ep_135.n88model python create_cantilever_ep.py -14.0 cantilever_ep_140.n88model python create_cantilever_ep.py -14.5 cantilever_ep_145.n88model python create_cantilever_ep.py -15.0 cantilever_ep_150.n88model
You probably want to put all these commands in a script or batch file.
And then we solve them all
faim --convergence_tolerance=1E-9 cantilever_ep_100.n88model faim --convergence_tolerance=1E-9 cantilever_ep_105.n88model faim --convergence_tolerance=1E-9 cantilever_ep_110.n88model faim --convergence_tolerance=1E-9 cantilever_ep_115.n88model faim --convergence_tolerance=1E-9 cantilever_ep_120.n88model faim --convergence_tolerance=1E-9 cantilever_ep_125.n88model faim --convergence_tolerance=1E-9 cantilever_ep_130.n88model faim --convergence_tolerance=1E-9 cantilever_ep_135.n88model faim --convergence_tolerance=1E-9 cantilever_ep_140.n88model faim --convergence_tolerance=1E-9 cantilever_ep_145.n88model faim --convergence_tolerance=1E-9 cantilever_ep_150.n88model
As we can see from the number of elements exceeding the plastic limit (the last column of the table), FAIM does indeed show plastic onset at 10 N load. The data from table Elastoplastic cantilever results are visualized in Figure 40. Agreement is very good until the onset of beam failure approaches. Then there begins to be a some divergence between FAIM and the analytic results. Better agreement can be obtained with a smaller element size, but fundamentally near the singularity of failure, there are very rapid changes in plastic strain through the cross-section, and these cannot be well modelled by numerical discretisation. However, away from this singularity, numerical results are good.
|
|
When running several models at different parameter points, it can become tedious to open each analysis file and search out the relevant quantity. We can use the n88tabulate tool to save some effort. In the present case, after we have solved all the models, the following command will generate the 4th column of the table (displacement as calculated by FAIM): n88tabulate -V dz_avg_ns2 *_analysis.txt The variable name for the desired quantity (here |
load |
tip displacement |
yielded |
||
|---|---|---|---|---|
linear |
analytic elastoplastic |
faim elastoplastic |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
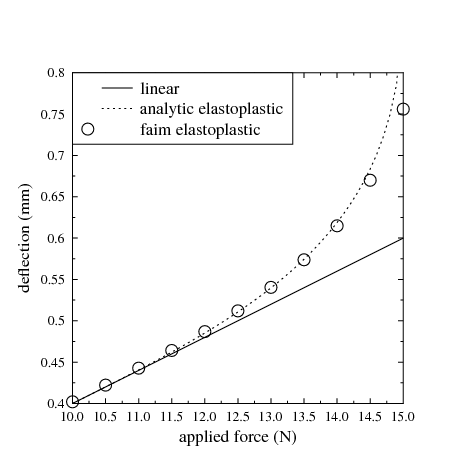
|
|
If you want, you can experiment with increasing the number of elements in the model (reducing the element size) to see how this affects the result. |
7.7.7. Incremental loading and hysteresis
Up to this point, we have solved a sequence of nonlinear models at different loads without giving a lot of thought about how these loads are applied. In fact we have solved each load point "from scratch". From a theoretical point of view, it would be better to start from the greatest load for which the model stays in the linear range, and then incrementally add small amounts of load, obtaining a sequence of slowly changing nonlinear solutions, each of which is used as the starting point for the solver for the subsequent load. This is discussed in Obtaining accurate nonlinear solutions by progressively applying loads. The question is, does this actually matter? Here we will investigate this and discover that the answer is "it depends".
The first thing we need is a script to take an existing
solved n88model file, and modify the applied force. You can find
this script, named modify_force.py, in the cantilever
subdirectory of the examples. Since you are getting by now pretty
good at scripts, here are all the preliminaries, up to
reading in an existing n88 model file:
from __future__ import division
import argparse
import vtk
import vtkbone
script_version = 1
parser = argparse.ArgumentParser (
description="""Take an existing cantilever model file, and modify the applied force
while leaving any existing solution unmodified. It can thus be used as the starting
value for a solution with the new applied force.""")
parser.add_argument ("input_file",
help="An existing cantilever model file.")
parser.add_argument ("applied_force", type=float,
help="The new applied force.")
parser.add_argument ("output_file",
help="Name for output file.")
args = parser.parse_args()
# Read existing model (including possible solution)
print(f"Reading n88model file: {args.input_file}")
reader = vtkbone.vtkboneN88ModelReader()
reader.SetFileName (args.input_file)
reader.Update()
model = reader.GetOutput()
Now, we could modify the numerical values of the force constraint, but from a programming view, it is easier to just delete it and re-create it.
# Delete the old applied force.
model.GetConstraints().RemoveItem("end_force")
# Apply the new force to the far end of the beam.
model.ApplyLoad(
"face_x1",
vtkbone.vtkboneConstraint.FACE_X1_DISTRIBUTION,
vtkbone.vtkboneConstraint.SENSE_Z,
args.applied_force,
"end_force")
That’s the meat of it. Now we just finish up with the usual entires to the history and the log, and write out the modified file.
# Update history and log
model.AppendHistory(f"Modified modify_force.py version {script_version} .")
model.AppendLog(
"""modify_force.py
Changed applied force on far face edge to {args.applied_force} .
Using vtkbone version {vtkbone.vtkboneVersion.GetvtkboneVersion()} .
"""
)
# Write an n88model file
print(f"Writing n88model file: {args.output_file}")
writer = vtkbone.vtkboneN88ModelWriter()
writer.SetInputData(model)
writer.SetFileName(args.output_file)
writer.Update()
|
|
Had we created the model with n88modelgenerator, it would have been even easier to change the load in the model file: n88modelgenerator can take as an input an existing model file, and it will preserve any existing solutions while modifying the material properties or constraints according to the command line arguments in the usual fashion. |
Now to run this, we first create and solve a nonlinear model as we did above, with an applied force that we know, from the previous analysis, is just at the limit of linear behaviour.
python create_cantilever_ep.py -10 cantilever_ep.n88model faim --convergence_tolerance=1e-9 cantilever_ep.n88model
As previously, we can extract from the analysis file just the numerical value for the deflection, like this
n88tabulate -V dz_avg_ns2 cantilever_ep_analysis.txt
which returns -4.020E-01.
Now we use our modify_force.py script to increase to applied
force to -10.5 .
python modify_force.py cantilever_ep.n88model -10.5 from_100_to_105.n88model
And we solve it and extract the new deflection.
faim --convergence_tolerance=1E-9 from_100_to_105.n88model
What we want to see, is that faim starts with the following two status lines:
Model contains elastoplastic material definitions. Model contains existing solution.
And further on, once the solver solver_sp itself has been launched,
we want to verify that we see the following status output:
Using existing solution as starting value.
Then, rinse and repeat until the desired final load is reached:
python modify_force.py from_100_to_105.n88model -11 from_105_to_110.n88model faim --convergence_tolerance=1E-9 from_105_to_110.n88model n88tabulate -V dz_avg_ns2 from_105_to_110_analysis.txt python modify_force.py from_105_to_110.n88model -11.5 from_110_to_115.n88model faim --convergence_tolerance=1E-9 from_110_to_115.n88model n88tabulate -V dz_avg_ns2 from_110_to_115_analysis.txt
and so on . . .
We can thus add another column to Elastoplastic cantilever results, and compare the “all-at-once” nonlinear solutions with the incremental solutions. Elastoplastic cantilever incremental results shows just these two columns. The results are practically indistinguishable. So can we therefore conclude that carefully applying an incremental load is pointless extra work? Not quite. We are not at the end of the story yet. Let us take our solution at a load of 14.5, and from there decrement the applied load back down to the linear region. Programmatically, this looks much like before:
python modify_force.py from_140_to_145.n88model -14 from_145_to_140.n88model faim --convergence_tolerance=1E-9 from_145_to_140.n88model python modify_force.py from_145_to_140.n88model -13.5 from_140_to_135.n88model faim --convergence_tolerance=1E-9 from_140_to_135.n88model
and so on . . .
We can tabulate all the deflections at once,
n88tabulate -V filename,dz_avg_ns2 *_analysis.txt
These additional load decreasing points are tabulated in Elastoplastic cantilever results for decreasing loads. These are plotted together with the increasing load points up to 14.5 in Figure 41. Now we see that that there is in fact a difference. Indeed we recognize the classic hysteresis curve. (Note that compared with Figure 40, we have swapped the axes, just so that it looks more conventional.)
| load | FAIM EP | FAIM incr |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| load | FAIM decr |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
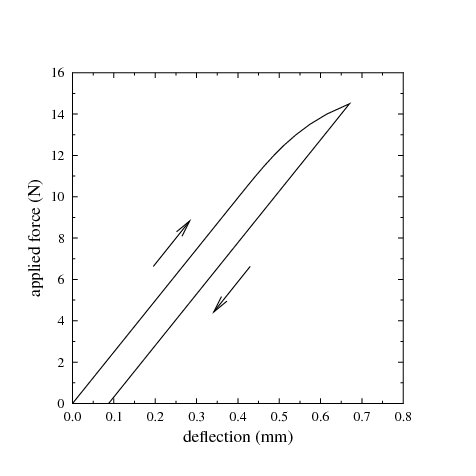
This concludes the tutorial on a cantilever with elastoplastic
material properties. We learned how to use elastoplastic materials
in vtkbone scripts, and also how to apply loads in incremental steps to
nonlinear models by modifying an existing n88model file. By
carefully applying incremental loading to the cantilever, we
determined that results were essentailly unaffected as compared with an
“all at once” solution for the initial deflection of the
beam, but that a residual deflection remains during the subsequent
unloading of the beam. This residual deflection, which is the hysteresis,
can only be observed by applying the load incrementally.
7.8. Advanced custom model: A screw pull-out test
In the preceding tutorials we were introduced to using vtkbone to create
original models that cannot be generated using
n88modelgenerator . We mentioned
that frequently the most challenging part of creating such
models is identifying the sets of nodes and/or elements
corresponding to the boundary conditions that
we desire. In that tutorial, however, we didn’t actually need to identify
any such sets ourselves, as we found that the standard node and element
sets as provided by vtkboneApplyTestBase were suitable for
our purposes. In this tutorial, by contrast, we will use
some sophisticated criteria for identifying the desired sets
for boundary conditions. This includes,
-
Identifying and characterizing features in the input image. Namely, we will determine the geometric location of a screw axis.
-
Identifying nodes by spatial location (distance from the screw, as well as depth from the top surface).
-
We will further reduce the selection of nodes based on visibility from a certain viewing angle, which is a useful technique for locating nodes on an uneven surface.
In the course of this example, we will generate the files screwpullout.py
and screwpullout.conf. You can find the completed versions of these files in
the examples/screwpullout directory of the distribution.
7.8.1. The model: a screw pull-out test
This example is a finite element model of an important mechanical test for orthopaedic biomechanics. This tutorial is based on the work of Stadelmann et al (2012). Physical tests were done in which a volume of bone substitute was constrained with a ring and the screw was pulled out. Here we construct a finite element model corresponding to this physical test.
The geometry of the model is in the file sawbone.aim in the data
directory of the distribution. It consists of a volume of bone substitute into which
a screw has been embedded. This is shown in Figure 42.
The data have been segmented such that
bone substitute is labelled with ID 127 (shown in beige), and the screw with ID 90
(shown in blue). The mechanical test is to find the force
required to pull out the screw.

|
|
The script will look for the data file sawbone.aim in
whatever directory it is run from. On your distribution, the example
script and the data file are in different directories, examples/screwpullout
and data respectively. We recommend that you copy the files from both
these directories to a temporary working directory for this tutorial.
|
7.8.2. Preliminaries: first lines of Python
Using your favourite text editor, create a file screwpullout.py.
By now you should be pretty familiar with importing the necessary Python modules:
from __future__ import division import os import sys import time import vtk import vtkbone
As before, we’ll also set a script version number:
script_version = n
| A version of this script has been used as a tutorial in previous versions of Faim. In Faim 9.0 we are on the nth iteration of this script. |
Since generating a model from a large micro-CT scan can take a lot of time, it is convenient to print status messages as the script proceeds, and to have these messages time stamped, so that we can see what steps potentially should be optimized (or where the script fails). The following function will take one or more strings and print them out one per line, with a time stamp on the first, and indenting the subsequent lines.
def message(msg, *additionalLines):
"""Print message with time stamp.
The first argument is printed with a time stamp.
Subsequent arguments are printed one to a line without a timestamp.
"""
print(f"{(time.time()-start_time):8.2f} {msg}")
for line in additionalLines:
print(" "*9 + line)
start_time = time.time()
7.8.3. Using a configuration file to store parameters
This model is going to be quite complicated. To keep things orderly,
we will put all our parameters in a configuration file. The
configuration file is a record of exactly which parameters were used to
generate a particular model. We’re going to write the configuration file
itself in Python code, so that we don’t have to write a file parser to read
it. Here is what the configuration file (screwpullout.conf) looks like:
# ------------------------------------------------------------------------- # Configuration file screwpullout.conf # # This configuration file is in the format of python source code. # If you stick with simple assignments, then it looks like a typical # configuration file, and can probably be read with other file parsers, # if you wish to do so. # Input image file. input_image_file = "sawbone.aim" # Output n88model file. # - take the input file name and change the extension to .n88model n88model_file = os.path.splitext(input_image_file)[0] + ".n88model" # Bone material bone_material_id = 127 bone_material_modulus = 6829.0 # 6829.0 MPa for bone bone_material_poissons_ratio = 0.3 # Screw material screw_material_id = 90 screw_material_modulus = 69000.0 # 69 GPa for Aluminum screw_material_poissons_ratio = 0.3 # Displacement (in physical length units of the model) applied to the screw # surface. screw_displacement = 0.01 # Ring radii for finding nodes of bone material to which we will apply the # constrained ring. inner_ring_radius = 4.5 outer_ring_radius = 7.0 # Max depth for finding nodes of bone material to which we will apply the # constrained ring. The max is measured from the highest node of constrained # bone found. bone_constraint_max_depth = 1.5
Now we add to our script the following:
-
A bit of code to get the configuration file name from the command line.
-
A few lines to execute the configuration file as Python code.
-
Some lines to print out all the values that we expected to read in. This is very good practice so when you run it, you can verify that everything is as you expect.
All that looks like this:
if len(sys.argv) != 2:
print("Usage: python screwpullout.py example.conf")
sys.exit(1)
config_file = sys.argv[1]
# Read in configuration file.
message("Reading configuration file " + config_file)
# Here we are actually executing it as python code.
with open(config_file) as f:
code = compile(f.read(), config_file, 'exec')
exec(code)
# Print out values that we read in. This also has the effect of causing
# this script to die if configuration values are missing (which is a good thing).
settings_text = ["Configuration:"]
settings_text.append( "input file = %s" % input_image_file)
settings_text.append( "output file = %s" % n88model_file)
settings_text.append( "bone material id = %s" % bone_material_id)
settings_text.append( "bone material Young's modulus = %s" % bone_material_modulus)
settings_text.append( "bone material Poisson's ratio = %s" % bone_material_poissons_ratio)
settings_text.append( "screw material id = %s" % screw_material_id)
settings_text.append( "screw material Young's modulus = %s" % screw_material_modulus)
settings_text.append( "screw material Poisson's ratio = %s" % screw_material_poissons_ratio)
settings_text.append( "screw displacement = %s" % screw_displacement)
settings_text.append( "inner ring radius = %s" % inner_ring_radius)
settings_text.append( "bone constraint max depth = %s" % bone_constraint_max_depth)
message(*settings_text) 
This is slightly advanced python, where the asterisk means that
we pass the list of N items (strings in this case) not as a single list
argument, but as N individual arguments. It just happens that given
the way we wrote our message function, this is the best thing to do
here. |
Now when we run our script, we also have to specify the name of the configuration file:
$ python screwpullout.py screwpullout.conf
7.8.4. Reading the segmented image file
We will use a vtkboneAIMReader to read the data file, which is in the Scanco AIM file format. This file contains a segmented image. As well, we want to add some additional lines to report our progress, and print some values as a sanity check.
message("Reading input data.")
reader = vtkbone.vtkboneAIMReader()
reader.SetFileName(input_image_file)
reader.DataOnCellsOn()  reader.Update()
image = reader.GetOutput()
message("Read %d points from image file." % image.GetNumberOfPoints())
image_bounds = image.GetBounds()
reader.Update()
image = reader.GetOutput()
message("Read %d points from image file." % image.GetNumberOfPoints())
image_bounds = image.GetBounds()  message("Image bounds:", (" %.4f"*6) % image_bounds)
message("Image bounds:", (" %.4f"*6) % image_bounds)
As discussed in several previous tutorials, we can either have the image
data on the Cells or the Points. vtkbone is
generally agnostic on this point, but it is good to be clear. |
|
| This is a standard VTK method for many types of VTK objects, returning an array of six values: xmin, xmax, ymin, ymax, zmin, zmax. |
The output so far, when we run the Python script, will look something like this:
$ python screwpullout.py screwpullout.conf
0.00 Reading configuration file screwpullout.conf
0.00 Configuration:
input file = sawbone.aim
output file = sawbone.n88model
bone material id = 127
bone material Young's modulus = 6829.0
bone material Poisson's ratio = 0.3
screw material id = 90
screw material Young's modulus = 69000.0
screw material Poisson's ratio = 0.3
screw displacement = 0.01
inner ring radius = 4.5
bone constraint max depth = 1.5
0.00 Reading input data.
0.07 Read 5775920 points from AIM file.
0.07 Image bounds:
11.9700 27.4740 11.7420 27.1320 0.1140 35.3400
7.8.5. Converting the image data to elements
As in the tutorial Compressing a cube revisited using vtkbone,
we need to convert
the input CT image data to a vtkUnstructuredGrid object representing the
geometry. Again, we will use a vtkboneImageToMesh filter for this purpose.
message("Converting to hexahedral cells.")
mesher = vtkbone.vtkboneImageToMesh()
mesher.SetInputData(image)
mesher.Update()
mesh = mesher.GetOutput()
message("Generated %d hexahedrons" % mesh.GetNumberOfCells())
7.8.6. Defining material properties
Once again, we repeat the steps of the tutorial
Compressing a cube revisited using vtkbone,
and we generate a material table and two materials: bone and
screw.
message ("Creating material table.")
material_table = vtkbone.vtkboneMaterialTable()
# Create an isotropic material for bone and add it to the table.
bone_material = vtkbone.vtkboneLinearIsotropicMaterial()
bone_material.SetName("bone")
bone_material.SetYoungsModulus(bone_material_modulus)
bone_material.SetPoissonsRatio(bone_material_poissons_ratio)
material_table.AddMaterial(bone_material_id, bone_material)
# Create an isotropic material for the screw and add it to the table.
screw_material = vtkbone.vtkboneLinearIsotropicMaterial()
screw_material.SetName("screw")
screw_material.SetYoungsModulus(screw_material_modulus)
screw_material.SetPoissonsRatio(screw_material_poissons_ratio)
material_table.AddMaterial(screw_material_id, screw_material)
7.8.7. Creating a vtkboneFiniteElementModel object
In the tutorial, Deflection of a cantilevered beam; adding custom boundary conditions and loads, we used vtkboneApplyTestBase to combine the geometry with the model table into a vtkboneFiniteElementModel object. vtkboneApplyTestBase didn’t create any displacement boundary conditions or applied loads for us, but it did define some standard sets that we subsequently used to define our displacement boundary conditions and applied load. This time, those standard sets won’t we very useful for us. So instead of vtkboneApplyTestBase , we’ll use an even more elementary model-creating filter called vtkboneFiniteElementModelGenerator , which creates a vtkboneFiniteElementModel object without any pre-defined sets.
|
|
Actually, it is not quite true that we couldn’t use need any standard sets. The standard set “face_z1” would be the top surface of the screw, which is one of the sets that we need. However, for the purposes of demonstration, we’ll show how to find that node set manually. |
message("Constructing a finite element model object.")
generator = vtkbone.vtkboneFiniteElementModelGenerator()
generator.SetInputData(0, mesh)
generator.SetInputData(1, material_table)
generator.Update()
model = generator.GetOutput()
model.ComputeBounds()  bounds = model.GetBounds()
message("Model bounds:", (" %.4f"*6) % bounds)
bounds = model.GetBounds()
message("Model bounds:", (" %.4f"*6) % bounds)
| Unlike vtkImageData objects, vtkUnstructuredGrid objects, from which vtkboneFiniteElementModel objects are derived, don’t know their bounds unless you explicitly request them to be computed. |
7.8.8. Writing an n88model file
Now that we have a vtkboneFiniteElementModel object, we can save it. Of course, the model isn’t finished yet, but just as in the previous tutorial, we can still save it and examine it as we go.
message("Writing file %s" % n88model_file)
writer = vtkbone.vtkboneN88ModelWriter()
writer.SetInputData(model)
writer.SetFileName(n88model_file)
writer.Update()
|
|
Once again, in everything that follows it is intended that you add
new lines to the script before the code (show just above) that saves
the model to a file. Otherwise of course the saved n88model file won’t
reflect our additions and changes.
|
7.8.9. Adding history and log fields
By now you’ll be familiar with adding History and Log fields to help us later trace back the details of the creation of this model. Let’s add all this information (before the code to save the file!):
model.AppendHistory("Created by screwpullout.py version %s ." % script_version)
model.AppendLog(
"""screwpullout.py
Model of screw being pulled out of bone substitute material.
Using VTKBONE version %s .
Configuration file : %s
""" % (vtkbone.vtkboneVersion.GetVTKBONEVersion(), config_file)
+ "\n".join(settings_text)) 
This looks a little bit complicated. "\n".join(settings_text))
converts the Python list of strings to a single long string,
inserting a line return ("\n") between each list item. We then just
add it to the other string. |
Now run the script. As a reminder, this is done with
$ python screwpullout.py screwpullout.conf
As shown in previous tutorials,
we can retrieve the History and Log fields from the n88model file
at any time with n88modelinfo:
$ n88modelinfo --history --log sawbone.n88model History: ---------------------------------------------------------------------- 2016-Sep-27 16:12:21 Created by screwpullout.py version 8 . ---------------------------------------------------------------------- Log: ---------------------------------------------------------------------- 2016-Sep-27 16:12:21 screwpullout.py Model of screw being pulled out of bone substitute material. Using vtkbone version 1.0 . Configuration file : screwpullout.conf Configuration: input file = sawbone.aim output file = sawbone.n88model bone material id = 127 bone material Young's modulus = 6829.0 bone material Poisson's ratio = 0.3 screw material id = 90 screw material Young's modulus = 69000.0 screw material Poisson's ratio = 0.3 screw displacement = 0.01 inner ring radius = 4.5 bone constraint max depth = 1.5 ----------------------------------------------------------------------
7.8.10. Determining the screw orientation
In order to properly apply the desired constraints, we will need to know where the screw is. We can do this algorithmically, by calculating the principal axes of inertia of the screw using vtkboneTensorOfInertia . We are going to assume that the principal axis closest to the z axis is the screw axis. This won’t be exactly true. Consider for example if the screw is cut off unevenly, then the principal axis of inertia won’t be exactly the same as the screw axis, but for our purposes, it is good enough.
message("Determining screw geometry.")
moi = vtkbone.vtkboneTensorOfInertia()
moi.SetInputData(image)
moi.SetSpecificValue(screw_material_id)  moi.Update()
message("Number of cells belonging to screw: %d" % moi.GetCount())
message("Volume of screw: %.2f" % moi.GetVolume())
screwCenterOfMass = (moi.GetCenterOfMassX(),
moi.GetCenterOfMassY(),
moi.GetCenterOfMassZ())
message("Center of mass of screw: %.5f, %.5f, %.5f" % screwCenterOfMass)
screwAxis = moi.GetPrincipalAxisClosestToZ()
message("Axis of screw: %.5f, %.5f, %.5f" % screwAxis)
screwDistanceToBoundary = (bounds[5] - screwCenterOfMass[2]) / screwAxis[2]
screwCenterAtBoundary = (
screwCenterOfMass[0] + screwDistanceToBoundary * screwAxis[0],
screwCenterOfMass[1] + screwDistanceToBoundary * screwAxis[1],
bounds[5])
moi.Update()
message("Number of cells belonging to screw: %d" % moi.GetCount())
message("Volume of screw: %.2f" % moi.GetVolume())
screwCenterOfMass = (moi.GetCenterOfMassX(),
moi.GetCenterOfMassY(),
moi.GetCenterOfMassZ())
message("Center of mass of screw: %.5f, %.5f, %.5f" % screwCenterOfMass)
screwAxis = moi.GetPrincipalAxisClosestToZ()
message("Axis of screw: %.5f, %.5f, %.5f" % screwAxis)
screwDistanceToBoundary = (bounds[5] - screwCenterOfMass[2]) / screwAxis[2]
screwCenterAtBoundary = (
screwCenterOfMass[0] + screwDistanceToBoundary * screwAxis[0],
screwCenterOfMass[1] + screwDistanceToBoundary * screwAxis[1],
bounds[5])  message("Distance from screw center of mass to top boundary: %.3f" % screwDistanceToBoundary)
message("Screw center at top boundary: %.3f, %.3f, %.3f" % screwCenterAtBoundary)
message("Distance from screw center of mass to top boundary: %.3f" % screwDistanceToBoundary)
message("Screw center at top boundary: %.3f, %.3f, %.3f" % screwCenterAtBoundary)
| This is how we limit the inertia tensor to be calculated only over the screw elements. | |
| This is a simple geometric calculation: given the center of mass of the screw and the direction of the screw axis, find the intersection with the upper bound of the model. |
Now we run it, and this part of the script generates output like this:
1.55 Determining screw geometry.
1.67 Number of cells belonging to screw: 449618
1.67 Volume of screw: 666.13
1.67 Center of mass of screw: 20.20622, 19.02016, 18.21310
1.67 Axis of screw: -0.00733, -0.00243, 0.99997
1.67 Distance from screw center of mass to boundary: 16.785
1.67 Screw center at boundary: 20.083, 18.979, 34.998
Comparing by eye with the rendering in ParaView, we can determine that these values are about right, so we give ourselves a gold star in advanced math and carry on.
7.8.11. Adding a boundary condition: applying a displacement to the screw end
We want to add a boundary condition to the screw where it intersects the
boundary of the model. All these nodes lie on a plane, so they are easily
found with the function AddNodesOnPlane provided in vtkboneNodeSetsByGeometry .
Note that these nodes get associated with the FE model object, and we have
to assign a name, in this case “screw_top”, so that we can refer later
to this set.
message("Adding the screw_top boundary condition.")
vtkbone.vtkboneNodeSetsByGeometry.AddNodesOnPlane(
2,  bounds[5],
bounds[5],  "screw_top",
"screw_top",  model,
screw_material_id)
model,
screw_material_id)  message("Found %d nodes belonging to screw_top" %
model.GetNodeSet("screw_top").GetNumberOfTuples())
message("Found %d nodes belonging to screw_top" %
model.GetNodeSet("screw_top").GetNumberOfTuples())
| The value 2 specified the z-axis (VTK and python being zero-indexed). | |
| This is zmax. | |
| The name of the node set we are creating. | |
| This argument is optional, and specifies that we only want nodes associated with material ID “screw_material_id”. This is not actually necessary for the given data, since no elements of other material IDs intersect the zmax surface. |
We want to be able to inspect this result, and ensure that we have in fact selected the nodes on the top of the screw. To do this, run the script to update the model file. Now, as in the tutorial Bending test of a radius bone with an uneven surface, we are going to use the tool n88extractsets to extract and visualize the node set.
$ n88extractsets sawbone.n88model Reading N88 Model file : sawbone.n88model Writing node set : sawbone_node_set_screw_top.vtp
The file sawbone_node_set_screw_top.vtp can be opened an visualized with ParaView.
The nodes are shown in Figure 43, exactly on the end of the screw.
This is what we want.

|
|
An alternative to using n88extractsets is to add lines to extract and save the node set directly to the script. We no longer recommend this, as it makes the script longer, more complex, and slower to run. However, for the record, this is how it would be done, writer = vtk.vtkXMLUnstructuredGridWriter()
writer.SetInputData(model.DataSetFromNodeSet("screw_top"))
writer.SetFileName("screw_top_nodes.vtu")
writer.Update()
|
Having verified that we have found the set of nodes that we want, we can use
the method ApplyBoundaryCondition of the vtkboneFiniteElementModel
object to create a boundary condition. Note that we also give this the
name “screw_top_displacement”.
model.ApplyBoundaryCondition(
"screw_top",  2,
2,  screw_displacement,
screw_displacement,  "screw_top_displacement")
"screw_top_displacement")
| The name of the set to which is applied the boundary condition. | |
| Once again the value 2 means the z direction | |
| This variable is the numerical value of the displacement. |
7.8.12. Fixing the nodes in a ring on the bone surface
This boundary condition is much more difficult, because we want to find nodes lying approximately in a ring on a rough surface. The approach we will take is to successively whittle down candidate nodes by applying a sequence of criteria, until we have finally just the nodes we want. These are the criteria:
-
Elements (cells) lie between a specified inner radius and outer radius, as measured from the screw axis.
-
Nodes lie within a maximum specified depth from the highest node satisfying the first criterion.
-
Nodes are visible from above.
|
|
These selection criterion could in principle be applied in a different order. The reason for doing the selection by visibility last, is that it is computationally expensive, so we want to whittle down the candidate nodes/elements as much as possible before applying a visibility test. |
VTK uses the concept of implicit functions which can be used to select points and cells within or without a certain geometry. Here we are going to use two vtkCylinder objects, and combine them with a difference operation with a vtkImplicitBoolean . This will result in a hollow cylinder. VTK has a filter object, vtkExtractGeometry , that will select points and cells based on a specified implicit function.
One complication is that set of Points in the output of vtkExtractGeometry are
different than the
original Points, and so the Point IDs will be different. However, we need to know the
original Point IDs in order to be able to apply boundary conditions to the FE model.
The solution to this is to use a concept in VTK called “Pedigree ID”. These
can be accessed with the method GetPedigreeIds from the PointData.
|
|
Not every VTK data set will have Pedigree IDs. They must be added to the data set before we start chopping out subsets. However, by default vtkboneFiniteElementModelGenerator creates vtkboneFiniteElementModel objects with Pedigree IDs. |
message("Adding the fixed_bone_surface boundary condition.")
inner_cylinder = vtk.vtkCylinder()  inner_cylinder.SetRadius(inner_ring_radius)
inner_cylinder.SetCenter(screwCenterAtBoundary[0], 0, screwCenterAtBoundary[1])
inner_cylinder.SetRadius(inner_ring_radius)
inner_cylinder.SetCenter(screwCenterAtBoundary[0], 0, screwCenterAtBoundary[1])  outer_cylinder = vtk.vtkCylinder()
outer_cylinder.SetRadius(outer_ring_radius)
outer_cylinder.SetCenter(screwCenterAtBoundary[0], 0, screwCenterAtBoundary[1])
outer_cylinder = vtk.vtkCylinder()
outer_cylinder.SetRadius(outer_ring_radius)
outer_cylinder.SetCenter(screwCenterAtBoundary[0], 0, screwCenterAtBoundary[1])  rotate_Y_to_Z = vtk.vtkTransform()
rotate_Y_to_Z = vtk.vtkTransform()  rotate_Y_to_Z.RotateX(90)
cylinder_difference = vtk.vtkImplicitBoolean()
cylinder_difference.AddFunction(outer_cylinder)
cylinder_difference.AddFunction(inner_cylinder)
cylinder_difference.SetOperationTypeToDifference()
cylinder_difference.SetTransform(rotate_Y_to_Z)
cylinder_extractor = vtk.vtkExtractGeometry()
cylinder_extractor.SetImplicitFunction(cylinder_difference)
cylinder_extractor.SetInputData(model)
cylinder_extractor.Update()
geometry_in_ring = cylinder_extractor.GetOutput()
rotate_Y_to_Z.RotateX(90)
cylinder_difference = vtk.vtkImplicitBoolean()
cylinder_difference.AddFunction(outer_cylinder)
cylinder_difference.AddFunction(inner_cylinder)
cylinder_difference.SetOperationTypeToDifference()
cylinder_difference.SetTransform(rotate_Y_to_Z)
cylinder_extractor = vtk.vtkExtractGeometry()
cylinder_extractor.SetImplicitFunction(cylinder_difference)
cylinder_extractor.SetInputData(model)
cylinder_extractor.Update()
geometry_in_ring = cylinder_extractor.GetOutput()  message("Found %d elements between inner and outer radii." % geometry_in_ring.GetNumberOfCells())
message("Found %d elements between inner and outer radii." % geometry_in_ring.GetNumberOfCells())
| Important: vtkCylinder is by default oriented with a y axis of rotation. We will rotate to z axis of rotation later. | |
| Note that the center is swapped y ↔ z because of the transform that will be applied. | |
| This is the transform we need to bring y → z. Note that the transformation will be applied to input points, not to the cylinder geometry. | |
| The output will be another vtkUnstructuredGrid, which consists of a subset of the input geometry (including a subset of both Cells and Points). |
Now, this is a good place to see what we have so far for a selection.
There are two possibilites: we could write out geometry_in_ring with
a vtkXMLUnstructuredGridWriter filter, or we could add the
element IDs as a set to the model. Let’s do the latter:
elements_in_ring = vtk.vtkIdTypeArray()elements_in_ring.DeepCopy(geometry_in_ring.GetCellData().GetPedigreeIds()) elements_in_ring.SetName("in_ring") model.AddElementSet(elements_in_ring)
To keep things clear, we’re going to make a copy of the data array
that is the PedigreeIds. This will allow us to modify it, by for
example re-naming it, without affecting the original. There are two steps
to this: creating a new empty vtkIdTypeArray and then using
its DeepCopy method on the data array we want to copy. |
Again, run the script to update the n88model file. We can now
extract this element set from it as follows:
$ n88extractsets --element_sets sawbone.n88model Reading N88 Model file : sawbone.n88model Writing element set : sawbone_element_set_in_ring.vtp
Figure 44 shows this selection (i.e. the file
sawbone_element_set_in_ring.vtp), together with the
screw elements, shown for context. (We used a Threshold filter in ParaView to
show just the screw cells from sawbone.n88model.) Figure 45 is another view of the same data. This view
is more suited to inspecting the ring geometry of our selection. To construct
this view, first hit the +z button on the toolbar in order to view exactly
along the z axis. Then from View Settings under the Edit menu, select Use
Parallel Projection. Finally, change the Representation of both data sets to
Surface With Edges in order to show individual Cells.


To select elements based on depth, as measured from the highest node in our set, we apply a similar approach as we did to select elements within the correct radii. We use a VTK implicit function, in this case a vtkBox , to specify the geometrical volume to which we want to limit our element set.
message("Filtering node set by depth.")
geometry_in_ring_bounds = geometry_in_ring.GetBounds()  message("Bounds of ring geometry: ", (" %.4f"*6) % geometry_in_ring_bounds)
box_bounds = (geometry_in_ring_bounds[0],
geometry_in_ring_bounds[1],
geometry_in_ring_bounds[2],
geometry_in_ring_bounds[3],
geometry_in_ring_bounds[5] - bone_constraint_max_depth,
geometry_in_ring_bounds[5])
message("Limiting selection to box bounds: ", (" %.4f"*6) % box_bounds)
box = vtk.vtkBox()
box.SetBounds(box_bounds)
filter = vtk.vtkExtractGeometry()
filter.SetImplicitFunction(box)
filter.ExtractInsideOn()
filter.ExtractBoundaryCellsOn()
filter.SetInputData(geometry_in_ring)
filter.Update()
geometry_depth_filtered_ring = filter.GetOutput()
message("Found %d elements in bounding box." % geometry_depth_filtered_ring.GetNumberOfCells())
message("Bounds of ring geometry: ", (" %.4f"*6) % geometry_in_ring_bounds)
box_bounds = (geometry_in_ring_bounds[0],
geometry_in_ring_bounds[1],
geometry_in_ring_bounds[2],
geometry_in_ring_bounds[3],
geometry_in_ring_bounds[5] - bone_constraint_max_depth,
geometry_in_ring_bounds[5])
message("Limiting selection to box bounds: ", (" %.4f"*6) % box_bounds)
box = vtk.vtkBox()
box.SetBounds(box_bounds)
filter = vtk.vtkExtractGeometry()
filter.SetImplicitFunction(box)
filter.ExtractInsideOn()
filter.ExtractBoundaryCellsOn()
filter.SetInputData(geometry_in_ring)
filter.Update()
geometry_depth_filtered_ring = filter.GetOutput()
message("Found %d elements in bounding box." % geometry_depth_filtered_ring.GetNumberOfCells())
Note that the zmax bound of geometry_in_ring will be at the
highest bit of bone in the ring. |
Now just as before, we can create a corresponding element set for the purposes of inspection:
elements_depth_filtered_ring = vtk.vtkIdTypeArray()
elements_depth_filtered_ring.DeepCopy(geometry_depth_filtered_ring.GetCellData().GetPedigreeIds())
elements_depth_filtered_ring.SetName("depth_filtered_ring")
model.AddElementSet(elements_depth_filtered_ring)
Run the script, and use n88extractsets to
extract the element sets, and it will create a new file,
sawbone_element_set_depth_filtered_ring.vtp.
Figure 46 shows the remaining elements after filtering by depth.
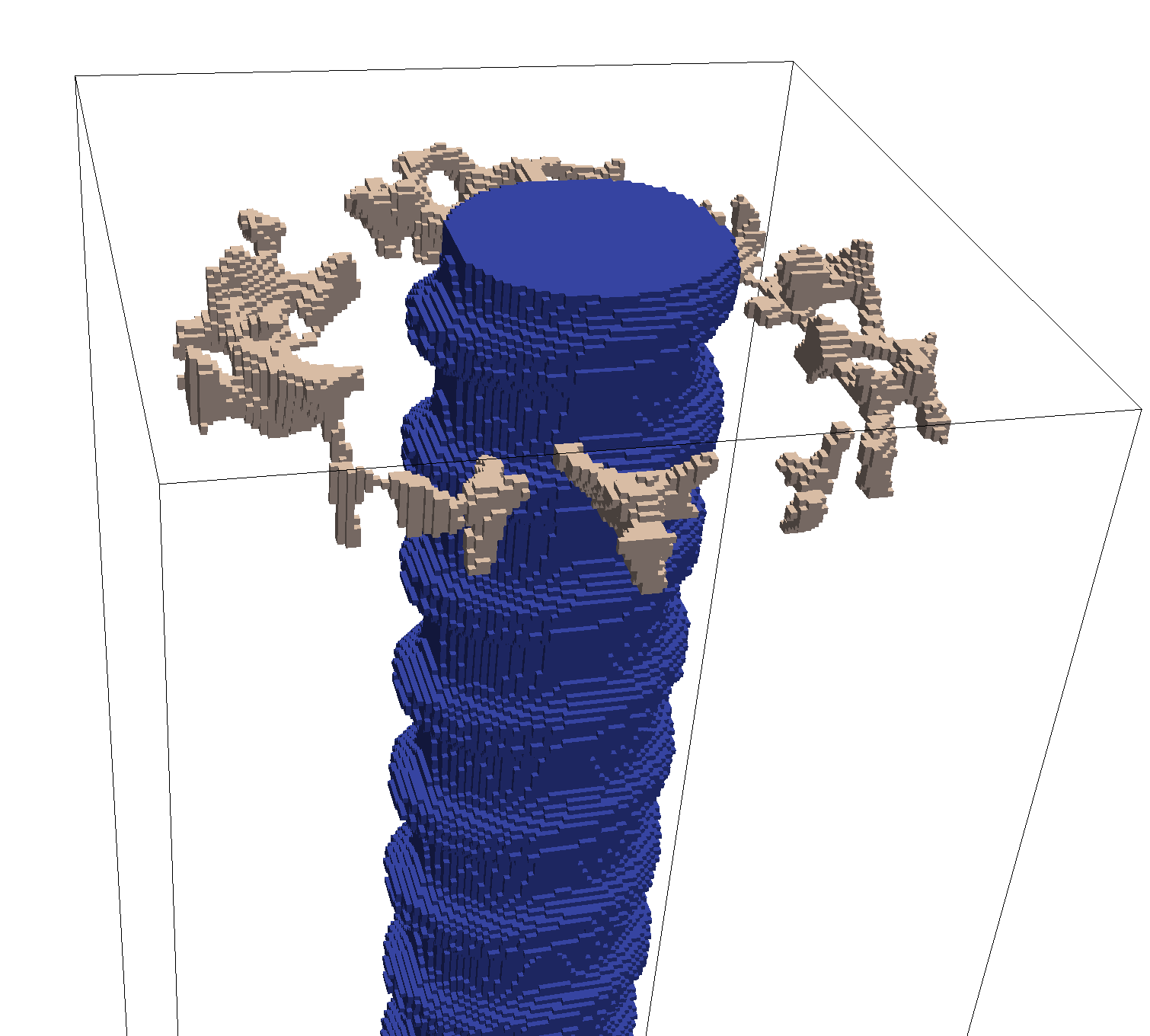
We can use the function FindNodesOnVisibleSurface from
vtkboneNodeSetsByGeometry for this purpose. We need to
pass it a normal vector for the viewing direction, as well as an empty
vtkIdTypeArray for storing the result.
message("Finding visible nodes.")
visibleNodesIds = vtk.vtkIdTypeArray()  normalVector = (0,0,1)
normalVector = (0,0,1)  vtkbone.vtkboneNodeSetsByGeometry.FindNodesOnVisibleSurface(
visibleNodesIds,
geometry_depth_filtered_ring,
normalVector,
bone_material_id)
vtkbone.vtkboneNodeSetsByGeometry.FindNodesOnVisibleSurface(
visibleNodesIds,
geometry_depth_filtered_ring,
normalVector,
bone_material_id)  visibleNodesIds.SetName("ring_top_visible")
model.AddNodeSet(visibleNodesIds)
message("Found %d visible nodes." % visibleNodesIds.GetNumberOfTuples())
visibleNodesIds.SetName("ring_top_visible")
model.AddNodeSet(visibleNodesIds)
message("Found %d visible nodes." % visibleNodesIds.GetNumberOfTuples())
| This will store the result as a list of Point IDs. | |
| This is the negative of the viewing direction. | |
FindNodesOnVisibleSurface automatically returns the Pedigree Ids,
provided that they exist on in input object (they do). |
Again, run the script to update the n88model file. This time we want
to extract the node sets
$ n88extractsets --node_sets sawbone.n88model Reading N88 Model file : sawbone.n88model Writing node set : sawbone_node_set_screw_top.vtp Writing node set : sawbone_node_set_ring_top_visible.vtp
The resulting ring-shaped cloud of points (file
sawbone_node_set_ring_top_visible.vtp) is shown in Figure 47.
These are the nodes to which we will apply our fixed boundary condition.

Now that we have a named node set for this constraint, it is easy to create the desired boundary condition, which we will name “fixed_bone_surface”:
model.FixNodes("ring_top_visible", "fixed_bone_surface")
7.8.13. Adding a convergence set
As we did in Tutorial: Deflection of a cantilevered beam; adding custom boundary conditions and loads, we will add a convergence set. See Convergence measure for discussion.
# Create a convergence set: the force on the screw
model.ConvergenceSetFromConstraint("screw_top_displacement")
This method notices that the constraint named screw_top_displacement, which we created previously, is a boundary condition. It then constructs the compliment, which is the force summed over all nodes subject to the boundary conditions. It is this force that the solver will watch to determine when its value ceases to change meaningfully. At that point the solver is finished.
7.8.14. Specifying sets for post-processing
Just as we saw in the tutorial
Deflection of a cantilevered beam; adding custom boundary conditions and loads,
there remains one more step to complete the n88model file,
and that is to identify the sets to
be used for post-processing calculations by n88postfaim.
We are interested in values calculated on the sets “ring_top_visible”
and “screw_top”. However, when we have generated our own custom sets,
as we have here, we must be careful about providing both node sets
and the corresponding element sets to n88postfaim. If
you review how we created the sets for generating boundary conditions,
you will observe that we only generated the node sets. Fortunately,
there is a method GetAssociatedElementsFromNodeSet of
vtkboneFiniteElementModel that will identify the corresponding
element set given a node set.
info = model.GetInformation()
pp_node_sets_key = vtkbone.vtkboneSolverParameters.POST_PROCESSING_NODE_SETS()
pp_elem_sets_key = vtkbone.vtkboneSolverParameters.POST_PROCESSING_ELEMENT_SETS()
for setname in ["ring_top_visible", "screw_top"]:
pp_node_sets_key.Append(info, setname)
elementSet = model.GetAssociatedElementsFromNodeSet(setname)
model.AddElementSet(elementSet)
pp_elem_sets_key.Append(info, setname)
After running the script, we can verify that these post-processing sets
are in fact specified in the n88model file,
$ n88modelinfo --problems sawbone.n88model Problems: ---------------------------------------------------------------------- Name : Problem1 Part : Part1 Constraints : screw_top_displacement,fixed_bone_surface PostProcessingNodeSets : ring_top_visible,screw_top PostProcessingElementSets : ring_top_visible,screw_top ----------------------------------------------------------------------
|
|
As before, it is possible to skip this step, and instead to specify the node and element sets to be used by n88postfaim on the command line of n88postfaim with the arguments --node_sets=ring_top_visible,screw_top --element_sets=ring_top_visible,screw_top |
We now have a complete n88model file. If you want, you can proceed to
solve it using faim, as in previous tutorials. We leave it
as an exercise to identify, from the analysis file, the net forces between
the screw top and the constrained ring of bone.
This concludes the screw pull-out tutorial. In this tutorial we learned how
to generate node sets based on complex criteria, to which we can then apply
boundary conditions. This is the final tutorial in the series on
learning vtkbone.
7.9. Tutorial: Radius compression with transformed boundary conditions for longitudinal bone strength estimates
In this tutorial, we will develop a Python script that can perform axial compression of a radius model from HR-pQCT, with boundary conditions that are transformed by the results of 3D rigid-body image registration. This application of Faim is used in a novel method for longitudinal estimates of bone strength, so-called “registered FE” (Plett et al. 2020 [in review]).
Briefly, the method was developed to take an image from a longitudinal series that has been registered (3D rigid-body image registration) and cropped to the largest common volume of bone captured in the image series. The boundary conditions of the FE model are transformed using the output from image registration (IPL, Scanco Medical AG) to ensure that the compression test is performed in the same orientation for all images in the series.
This tutorial uses vtkbone in a custom script that generates an n88model file. It is highly recommended to complete Tutorial: Compressing a cube revisited using vtkbone before proceeding to this tutorial.
This tutorial will include:
-
vtkbone: How to initialize boundary conditions on an uneven load surface, such as when using a 3D registered bone volume from longitudinal HR-pQCT. -
vtkbone: How to transform boundary conditions and apply them to your finite element model. -
Example: “Registered FE” on a distal radius segment.
This tutorial assumes:
-
You have a basic understanding of Python scripting and Faim.
-
You have at least completed Tutorials 7.1-5 in this manual.
-
You are familiar with 3D image registration and its outputs, specifically the implementation used for longitudinal HR-pQCT images.
Registered FE is currently implemented using Python-based tools, packaged in Preparing Finite Element Models with vtkbone, to create custom finite element models that can be solved with Faim.
|
|
If you do not wish to build the script on your own as you follow this tutorial, a finished version is provided in the tutorial files (http://numerics88.com/downloads/). |
7.9.1. Script setup
We will write the script in the following sequence:
-
Import packages.
-
Define utility functions.
-
Define model generator function.
-
Define and call main function.
Start by opening a new script file titled “_modelgenerator_registered_fe.py_” (or another name that describes the purpose of the script).
Now we will import the packages that are needed for this script. Any additional packages that you wish to use may be added below this list:
import os import sys import argparse import numpy as np import vtk import vtkbone # additional packages can be added here
|
|
If you provide an alias for a package (e.g. “np” for “numpy”, as shown above) the alias should be used consistently throughout the script to avoid confusion. |
Let’s give the script a quick test run to make sure everything is installed correctly:
$ python modelgenerator_registered_fe.py
Running this script should result in no output, so any output will indicate an error with the import commands. Most often, any errors that occur at this point are likely triggered by a package that is not installed in your Python environment, or your Python environment is not activated.
7.9.2. Optional function: Messages with a time stamp
A useful addition to any script, particularly a script with many sequential steps, is a utility function that can output messages (i.e. warnings, errors, other key outputs) with a time stamp. This can make debugging easier, but can also help you pinpoint errors that do not throw obvious errors in the code (e.g. flawed image data that leads to unusual FE results).
Though there are many ways to accomplish this in Python, a utility function presents an excellent modular approach:
def message(msg, *additionalLines):
“””Print message with time stamp.
The first argument is printed with a time stamp.
Subsequent arguments are printed one to a line without a time stamp.
“””
print(('{0:8.2f} {1:s}'.format(time.time() - start_time,msg)))
for line in additionalLines:
print((" " * 9 + line))
|
|
You will need to import the time package (import time) with the packages we imported earlier.
|
We can also initialize the time stamp after this point:
start_time = time.time()
7.9.3. Utility function: Read a material file
The registered FE method currently uses custom bone volumes from the XtremeCT II systems (insert bone image), so a material file makes it easy to identify the loading surfaces and assign material properties to the bone volume. For more details on creating material files, see Material definitions file.
Our material file will have the following format:
MaterialDefinitions:
Surface:
Type: LinearIsotropic
E: 8748  nu: 0.3
Bone:
Type: LinearIsotropic
E: 8748
nu: 0.3
MaterialTable:
127: Surface
125: Bone
nu: 0.3
Bone:
Type: LinearIsotropic
E: 8748
nu: 0.3
MaterialTable:
127: Surface
125: Bone
| This is a typical modulus used for XtremeCT II images. |
|
|
A copy of this material file is stored with the tutorial files with the name “material_cort_trab_xt2_reg.txt”. |
Now that we have a material file, we need to define a function that can read it for our model generator.
def ReadMaterialFile(material_file):
# Initialize material names and identifiers:
bone_name = 'Bone'
surface_name = 'Surface'
bone_material_id = 125
surface_material_id = 127
# Read material_file and extract modulus and Poisson’s ratio:
with open(material_file, encoding='cp1250') as searchfile:
for line in searchfile:
front = line.split(':')[0]
if ("E" in front):
bone_modulus = float(line.split(':')[1])
surface_modulus = bone_modulus
if ("nu" in front):
bone_poissons_ratio = float(line.split(':')[1])
surface_poissons_ratio = bone_poissons_ratio
# Return material parameters to the model generator function:
return bone_name, bone_material_id, bone_modulus, bone_poissons_ratio, surface_name, surface_modulus, surface_poissons_ratio, surface_material_id
This function defines material names and identifiers based on the labels found in the bone volumes, then reads the material properties (i.e. modulus and Poisson’s ratio) from the material file. These properties will be assigned to the FE model via a material table in subsequent steps.
To read the file, the function searches through each line in the material file to identify and extract the elastic modulus and the Poisson’s ratio. After reading the file, the material properties of the bone and load surfaces are returned.
7.9.4. Model generator function: First steps
The most important function in this script is the model generator function, which follows this sequence:
-
Read the input image
-
Read/generate a transformation matrix to transform boundary conditions
-
Generate a voxel-based mesh and apply material properties from the material file
-
Define boundary conditions
-
Write the finite element model to an output file for the FE solver
We want to read a standard HR-pQCT image file (AIM), so we will use vtkboneAIMReader(). Note the use of the message() function we defined earlier.
def CreateN88Model(input_file, output_file, material_file, transform_file, overwrite, displacement):
# Optional file checks ---
# Ask the user if output_file should be overwritten:
if os.path.isfile(output_file) and not overwrite:  result = eval(input('File \"{}\" already exists. Overwrite? [y/n]: '.format(output_file)))
if result.lower() not in ['y', 'yes']:
print('Not overwriting. Exiting...')
os.sys.exit()
# Check that input_file exists:
if not os.path.isfile(input_file):
result = eval(input('File \"{}\" already exists. Overwrite? [y/n]: '.format(output_file)))
if result.lower() not in ['y', 'yes']:
print('Not overwriting. Exiting...')
os.sys.exit()
# Check that input_file exists:
if not os.path.isfile(input_file):  os.sys.exit('[ERROR] File \"{}\" not found!'.format(input_file))
# Read input_file:
message("Reading AIM file " + input_file + " as input...")
reader = vtkbone.vtkboneAIMReader()
reader.SetFileName(input_file)
reader.DataOnCellsOn()
reader.Update()
image = reader.GetOutput()
# Check that input_file is read correctly:
if not reader.GetOutput():
message("[ERROR] No image data read!")
sys.exit(1)
# Report image size (bounds):
message("Image bounds:", (" %.4f" * 6) % image.GetBounds())
os.sys.exit('[ERROR] File \"{}\" not found!'.format(input_file))
# Read input_file:
message("Reading AIM file " + input_file + " as input...")
reader = vtkbone.vtkboneAIMReader()
reader.SetFileName(input_file)
reader.DataOnCellsOn()
reader.Update()
image = reader.GetOutput()
# Check that input_file is read correctly:
if not reader.GetOutput():
message("[ERROR] No image data read!")
sys.exit(1)
# Report image size (bounds):
message("Image bounds:", (" %.4f" * 6) % image.GetBounds())
| If an output file already exists, the user may indicate whether or not the file should be overwritten. This is an optional step. | |
| The script will stop with an error message if the input file is not found. This is an optional code segment. |
|
|
All code segments related to this function (i.e. written below) must be nested within the function. Be mindful of proper indentation to avoid errors, particularly if you copy-paste the code segments in this document into a text editor. |
Now we want to define the transformation matrix by which we will transform the our boundary conditions of our model. For longitudinal image data, this transformation will likely be in the form of a 4x4 affine matrix that is returned from 3D rigid-body image registration. This matrix contains the rotations and translations that are required to align two images (typically, follow-up images aligned to the baseline orientation). In the SCANCO implementation of image registration, the matrix is stored within a text file, as shown below.
SCANCO TRANSFORMATION DATA VERSION: 10 R4_MAT: 9.9992300E-01 1.0839380E-02 -6.0423953E-03 -5.5105441E-01 -1.0396725E-02 9.9756137E-01 6.9016078E-02 2.8265885E+00 6.7757516E-03 -6.8947942E-02 9.9759725E-01 3.9438124E+00 0.0000000E+00 0.0000000E+00 0.0000000E+00 1.0000000E+00
To rotate the boundary conditions of any follow-up images (in a given image series) with respect to the baseline image, you will need to extract the 3x3 rotation matrix (the 9 elements in the upper-left of the 4x4 affine matrix) by adding the following lines to our CreateN88Model() function:
if os.path.isfile(transform_file):message("Reading IPL transformation matrix...") if(transform_file): t_mat = np.loadtxt(fname=transform_file, skiprows=2) rotation = t_mat[:3, :3] else:
message("[WARNING]No transformation matrix applied...") rotation = np.identity(3)
| This code segment is specifically designed for transformation matrices generated by 3D registration in IPL (SCANCO Medical AG) for XtremeCT II images. If you are reading a transformation matrix that has a different format than the one above, you will need to modify this code accordingly. | |
The else statement has been added to allow the user to skip the transformation step altogether. This is primarily to allow users to analyze baseline images with the same script as the follow-up images. |
Now would be a good time to read the material file by calling the function we defined earlier. Remember to place this code segment within the CreateN88Model() function.
if os.path.isfile(material_file):
bone_name, bone_material_id, bone_modulus, bone_poissons_ratio, surface_name, surface_modulus, surface_poissons_ratio, surface_material_id = ReadMaterialFile(material_file)
# Report error if file is missing or not read correctly:
else:
message("[ERROR] No material data read!")
sys.exit(1)
# Report material properties so the user can check values:  message('Material attributes:',
'{:16s} = {:>8s}'.format('Material name', bone_name),
' {:14s} = {:8d}'.format('ID', bone_material_id),
' {:14s} = {:8.2f} MPa'.format('Modulus', bone_modulus),
' {:14s} = {:8.2f}'.format('Poissons ratio', bone_poissons_ratio),
'{:16s} = {:>8s}'.format('Material name', surface_name),
' {:14s} = {:8d}'.format('ID', surface_material_id),
' {:14s} = {:8.2f} MPa'.format('Modulus', surface_modulus),
' {:14s} = {:8.2f}'.format('Poissons ratio', surface_poissons_ratio))
message('Material attributes:',
'{:16s} = {:>8s}'.format('Material name', bone_name),
' {:14s} = {:8d}'.format('ID', bone_material_id),
' {:14s} = {:8.2f} MPa'.format('Modulus', bone_modulus),
' {:14s} = {:8.2f}'.format('Poissons ratio', bone_poissons_ratio),
'{:16s} = {:>8s}'.format('Material name', surface_name),
' {:14s} = {:8d}'.format('ID', surface_material_id),
' {:14s} = {:8.2f} MPa'.format('Modulus', surface_modulus),
' {:14s} = {:8.2f}'.format('Poissons ratio', surface_poissons_ratio))
| This is an optional step to make sure our material properties have been read correctly. |
Since we have processed all our inputs, we can now create a finite element mesh from our image. We will apply a connectivity filter to our image, to make sure the model comprises a single object (i.e. with no floating pieces of bone or image noise in the model).
message("Applying connectivity filter...")
confilt = vtkbone.vtkboneImageConnectivityFilter()
confilt.SetInputData(image)
confilt.Update()
image = confilt.GetOutput()
Let’s mesh our image:
message("Generating mesh...")
mesher = vtkbone.vtkboneImageToMesh()
mesher.SetInputData(image)
mesher.Update()
mesh = mesher.GetOutput()
To apply the material properties to the mesh we just created, we will need to make a material table. This process takes the elastic modulus and Poisson’s ratio that we read from the material file and assigns them to a linear-elastic material in the table.
message("Generating material table...")
E = bone_modulus
v = bone_poissons_ratio
material_name = bone_name
linear_material = vtkbone.vtkboneLinearIsotropicMaterial()
linear_material.SetYoungsModulus(E)
linear_material.SetPoissonsRatio(v)
linear_material.SetName(material_name)
material_table = vtkbone.vtkboneMaterialTable()
material_table.AddMaterial(surface_material_id,linear_material)
material_table.AddMaterial(bone_material_id,linear_material)
We apply the material parameters to the mesh by compiling the mesh and material table into an initialized form of the finite element model, a “test base”.
message("Compiling model...")
# Compile the mesh and material_table into a test base:
modelConfig = vtkbone.vtkboneApplyTestBase()
modelConfig.SetInputData(0, mesh)
modelConfig.SetInputData(1, material_table)
Then we can tell Faim to identify the load surfaces, which are voxels/elements labeled with the number 127.
# Assign material_table properties to the appropriate voxels: modelConfig.SetTopConstraintSpecificMaterial(127) modelConfig.UnevenTopSurfaceOn() modelConfig.UseTopSurfaceMaximumDepthOn() modelConfig.SetTopSurfaceMaximumDepth(3.5)modelConfig.SetBottomConstraintSpecificMaterial(127) modelConfig.UnevenBottomSurfaceOn() modelConfig.UseBottomSurfaceMaximumDepthOn() modelConfig.SetBottomSurfaceMaximumDepth(3.5) modelConfig.Update() model = modelConfig.GetOutput() # Report model size (bounds): message("Model bounds:", (" %.4f" * 6) % model.GetBounds())
| 3.5 mm was chosen as a distance slightly less than half of the standard XtremeCT II image volume (10.2 mm). |
7.9.5. Model generator function: Apply transformed boundary conditions
Applying transformed boundary conditions is relatively simple and requires only a few additional lines of code from a standard “non-registered” test.
First, we need to define a displacement vector for the model.
message("Defining displacement boundary conditions...")
# Initialize the displacement vector:
e_init = np.array([0, 0, -float(displacement)])  # Fix the bottom surface nodes of the model, completely:
model.FixNodes('face_z0', 'bottom_fixed')
# Fix the bottom surface nodes of the model, completely:
model.FixNodes('face_z0', 'bottom_fixed') 
Remember that we use “+np+” as an alias for the numpy package. |
|
| Since we are rotating the applied displacement, we need to use axial boundary conditions. This means the fixed surface must be fixed in every direction. A uniaxial boundary condition would be complex and require nodes to translate within a plane defined perpendicular to the loading direction. A future challenge! |
The displacement vector is typically oriented along the z-axis and has a magnitude of 0.102 mm, 1% of the image “thickness”, for a standard XtremeCT II bone model (to achieve 1% apparent strain).
Since we are transforming the boundary conditions of follow-up images, so they are aligned in the same direction as the baseline image, the displacement vector needs to be transformed with the rotation matrix we generated earlier.
# Transform the displacement vector:
message("Setting boundary conditions...")
e_trafo = np.dot(np.linalg.inv(rotation), e_init)
|
|
Even though we are transforming the displacement vector, the magnitude will remain the same (i.e. 0.102mm). In the registered FE method, the magnitude of “+displacement+” can also be changed to reflect the reduction in image thickness by 3D image registration. |
Now we want to create a set of boundary conditions on the load surface, using the transformed displacement vector we just created. We will do this using the ApplyBoundaryCondition() function from vtkbone.
# Apply boundary conditions by components of the displacement vector:
model.ApplyBoundaryCondition('face_z1', vtkbone.vtkboneConstraint.SENSE_X, e_trafo[0], 'x_moved')  model.ApplyBoundaryCondition('face_z1', vtkbone.vtkboneConstraint.SENSE_Y, e_trafo[1], 'y_moved')
model.ApplyBoundaryCondition('face_z1', vtkbone.vtkboneConstraint.SENSE_Z, e_trafo[2], ‘z_moved')
model.ApplyBoundaryCondition('face_z1', vtkbone.vtkboneConstraint.SENSE_Y, e_trafo[1], 'y_moved')
model.ApplyBoundaryCondition('face_z1', vtkbone.vtkboneConstraint.SENSE_Z, e_trafo[2], ‘z_moved')
Make sure the vector components (x in e_trafo[0]; y in e_trafo[2]; z in e_trafo[2]) match the corresponding boundary condition (SENSE_X, SENSE_Y, SENSE_Z). |
7.9.6. Model generator function: Define model outputs and write n88model file
Before writing the n88model file, we want to define the model outputs that will be recorded when the model is solved. So, we will define the node sets from which we acquire our bone strength estimates (e.g. reaction force), specifically the top and bottom surfaces (loaded and fixed) of the model we just created.
info = model.GetInformation()
pp_node_sets_key = vtkbone.vtkboneSolverParameters.POST_PROCESSING_NODE_SETS()
pp_node_sets_key.Append(info, 'face_z1') # top surface nodes
pp_node_sets_key.Append(info, 'face_z0') # bottom surface nodes
model.AppendHistory("Created with modelgenerator_registered_fe.py version 1.0")
Almost there! The last step in this function is to write the model to an n88model file. The filename will be defined by an input variable “+output_file+”.
message("Writing n88model file: ", output_file)
writer = vtkbone.vtkboneN88ModelWriter()
writer.SetInputData(model)
writer.SetFileName(output_file)
writer.Update()
7.9.7. Main function: Process input variables and call model generator function
The main function of this script processes the user’s inputs and sends them to the model generator function to create our n88model file. The input arguments will be defined with an argument parser, including mandatory and optional variables. We can also include (brief) help documentation for the user to clarify what input variables are required for this script to run properly.
The input arguments we will define are:
-
Input file (required): A segmented AIM file.
-
Output file (required): The output filename.
-
Material file (required): The material file.
-
Transform file (optional): The 4x4 transformation file from 3D image registration (*.txt). Remember, this is not required if processing a baseline image and an identity matrix will be used instead.
-
Overwrite (optional): Overwrite existing output_file. Remember, the program will ask if
overwriteis not indicated andoutput_fileexists. -
Displacement (optional): Value to initialize displacement vector; default is 0.102 mm.
Written in code, this function will look like this:
# Main function
def main():
description = '''Generates an n88model from 3D registered images.
If no valid transform file is found, then no transform is applied.
Authors: Ryan M. Plett and Steven K. Boyd'''
parser = argparse.ArgumentParser(formatter_class = argparse.RawTextHelpFormatter, prog = 'blmodelgenerator_reg', description = description)
parser.add_argument('input_file', help = 'Input image file AIM).')
parser.add_argument('output_file', help = 'Output n88model file (*.n88model).')
parser.add_argument('--material_file', help = 'Material property file (*.txt).')
parser.add_argument('--transform_file', default = 'dummy', help = 'Transformation matrix (*.txt).')
parser.add_argument('--overwrite', action = 'store_true', help = 'Overwrite existing output.')
parser.add_argument('--displacement', type = float, default = '0.102', help = 'Displacement boundary condition for registered volume (LCV).')
args = parser.parse_args()
CreateN88Model(**vars(args))
To end the script, it is important to make sure all of these functions will actually be called by the program when it is run from the command line. This is done by a short code segment that checks to make sure the script has been run correctly from the command line.
# Call main function
if __name__ == '__main__':
main()
7.9.8. Example: Registered FE in practice
Now we will put this method into practice. We will test this script, using a registered XtremeCT II image (distal radius) and performing a standard compression test to 1% apparent strain.
You will need the following files, provided in the tutorial files ( http://numerics88.com/downloads/ ):
-
input_file:
REPO_004_RR_S4_REG_HOM_LS.AIM -
transform_file:
REPO_004_RR_S4_REG.TXT -
material_file:
material_cort_trab_xt2_reg.txt
The image file is an XtremeCT II image of a distal radius. The radius was imaged four times and each follow-up image (S2, S3, and S4) were misaligned from the baseline image (S1). The images were registered with 3D rigid-body image registration, identifying the the largest common volume (% overlap) between scans. For this radius, the volume was found to be 91.37% of the original bone volume. We will use this value to determine our compressive displacement for the test.
The transform file contains the affine transformation that is needed to transform the image (S4) to baseline (S1); therefore, each follow-up image will have the same volume (defined by the overlap) and different transformation files.

Let’s run our script in “help” mode (-h) to make sure we have all the inputs:
$ Python modelgenerator_registered_fe.py -h
usage: blmodelgenerator_reg [-h] [--material_file MATERIAL_FILE]
[--transform_file TRANSFORM_FILE] [--overwrite]
[--displacement DISPLACEMENT]
input_file output_file
Generates an n88model from 3D registered images.
If no valid transform file is found, then no transform is applied.
Authors: Ryan M. Plett and Steven K. Boyd
positional arguments:
input_file Input image file (*.AIM).
output_file Output n88 model file (*.n88model).
optional arguments:
-h, --help show this help message and exit
--material_file MATERIAL_FILE
Material property file (*.txt).
--transform_file TRANSFORM_FILE
Transformation matrix (*.txt).
--overwrite Overwrite existing output.
--displacement DISPLACEMENT
Displacement boundary condition for registered volume.
|
|
Make sure you activate your anaconda environment before executing the script. |
Here we can see the information that we added to the main function in our script with the argument parser. From this, we know that we are still missing the output_file and displacement arguments.
We will set the output filename to be the same as the input, just with the “n88model” extension instead of AIM, so it will look something like: REPO_004_RR_S4_REG_HOM_LS.n88model .
The volume of this image is 91.37% of the standard image volume (thickness 10.2mm), so we will scale the input displacement to be 91.37% of the standard displacement (0.102 mm): \(0.9137*0.102mm = 0.093mm\) . Calculating the displacement in this way provides a simplified “scaling factor” so that the apparent strain remains close to 1% for every scan in a study.
Now that we have all our inputs organized, let’s test our script:
$ Python modelgenerator_registered_fe.py REPO_004_RR_S4_REG_HOM_LS.AIM REPO_004_RR_S4_REG_HOM_LS.n88model --material_file material_cort_trab_xt2_reg.txt --transform_file REPO_004_RR_S4_REG.TXT --overwrite --displacement 0.093
If the script ran correctly, the output should look something like this:
0.00 Reading AIM file REPO_004_RR_S4_REG_HOM_LS.AIM as input...
0.10 Image bounds:
49.2881 67.5587 46.0103 69.4404 0.0000 10.1970
0.10 Reading IPL transformation matrix...
0.11 Material attributes:
Material name = Bone
ID = 125
Modulus = 8748.00 MPa
Poissons ratio = 0.30
Material name = Surface
ID = 127
Modulus = 8748.00 MPa
Poissons ratio = 0.30
0.11 Applying connectivity filter...
0.63 Generating mesh...
1.97 Generating material table...
1.97 Compiling model...
21.02 Model bounds:
49.5309 67.4373 46.1317 69.0762 0.0000 9.4079
21.02 Defining displacement boundary conditions...
21.02 Setting boundary conditions...
21.02 Writing n88model file:
REPO_004_RR_S4_REG_HOM_LS.n88model
257.88 Done. Have a nice day! 
It’s never a bad idea to have a little fun with your scripts. The message() function can make your day sometimes. :) |
A warning may appear while the script is run,
Warning: In ../Filters/Extraction/vtkValueSelector.cxx, line 547 vtkValueSelector (0x7fa8e6dbecd0): Warning: range selections should use two-component arrays to specify the range. Using single component arrays with a tuple for the low and high ends of the range is legacy behavior and may be removed in future releases.
This is nothing to worry about and will not affect the results of the script.

You can now solve the model with faim:
faim [additional options] [n88model file]
| See the faim reference documentation for details on the additional arguments that can be used. |
7.9.9. Post-processing
Once your n88model is solved, the results will need to be processed using a slightly altered procedure than in a typical “non-registered” analysis. The non-registered analysis extracts the results as the vertical component only (i.e. the z-component, as in reaction force, displacement, etc.), since the test is conducted in exactly the vertical direction. With the registered approach, the results are transformed and so the test is no longer conducted in the vertical direction alone; therefore, the resulting estimates must include all components (i.e. x-, y-, z-components). To do so, we will take the magnitude of a result (u) as:
If the model used in our example above was solved correctly, the reaction force results (see REPO_004_RR_S4_REG_HOM_LS_analysis.txt) should look something like this:
============================================================================
Table 9: Nodal Forces
----------------------------------------------------------------------------
Node set: 1
Name: face_z1
............................................................................
Fx Fy Fz
total -9.520E+01 3.637E+02 -8.214E+03
average -3.430E-03 1.310E-02 -2.959E-01
std_dev 1.583E-01 1.508E-01 4.905E-01
minimum -2.011E+00 -1.950E+00 -8.329E+00
maximum 2.694E+00 3.698E+00 3.189E-01
median -5.603E-06 0.000E+00 -7.541E-02
Let’s say that we want to find the “registration-adjusted” reaction force estimate. Instead of using the total z-component of the reaction force (-8.214 kN), we want to calculate the total reaction force magnitude as:
This operation accounts for the transformed boundary conditions and allows us to report precise estimates of bone strength from longitudinal data. The easiest way to implement this adjustment is to calculate the magnitude of an estimate after the results have been parsed into a delimited file or spreadsheet for statistical analysis in Excel, SPSS, or R.
To calculate failure load with n88pistoia we will need to use a modified command than would be used in a standard analysis:
n88pistoia [n88model file name] --constraint z_moved --critical_volume 2.0 --critical_strain 0.007 --output_file [pistoia file name]
From our example, this command should then look like:
n88pistoia REPO_004_RR_S4_REG_HOM_LS.n88model --constraint z_moved --critical_volume 2.0 --critical_strain 0.007 --output_file REPO_004_RR_S4_REG_HOM_LS_pistoia.txt
The constraint z_moved is a custom constraint that we added in the CreateN88Model function. The default for n88pistoia is “top_moved”, so be sure to use the correct constraint in your test. |
The full results set from this example can be parsed from the results files (*_analysis.txt or *_pistoia.txt) using the following commands:
$ n88tabulate -H -o [output_file] REPO_004_RR_S4_REG_HOM_LS_analysis.txt #OR $ $ n88tabulate -H -V "pis_fx_fail,pis_fy_fail,pis_fz_fail" -o [output_file] REPO_004_RR_S4_REG_HOM_LS_pistoia.txt
This concludes the tutorial! You should now be able to transform displacement boundary conditions using vtkbone and inputs from 3D image registration. The example included in this tutorial is representative of the analysis that can be performed on a standard single-stack (10.2 mm) radius or tibia image from XtremeCT II.
7.10. Additional examples
In addition to the tutorials, there are additional examples included in
the other_examples directory. Currently these consist of
- segment_dicom
-
An example of reading a raw image file and performing a simple segmentation based on a density threshold and connectivity.
8. Special Topics
8.1. Efficient Handling of Large Numbers of Material Definitions
In typical usage of Faim, the number of defined materials is small. In fact, often we define just a single material as “bone”. We can, and do, take advantage of the expectation of relatively few defined materials in the following three ways:
-
The solver can pre-calculate important values for each material. In particular, the standard solver pre-calculates a 24×24 local stiffness matrix for each material. This saves quite a bit of time on each iteration, and the storage is insignificant, provided that the number of material definitions is substantially less than the number of elements.
-
In the n88model file format, each individual material definition is stored as a kind of object, with a name, a named type, and named characteristics and values. This allows great flexibility in defining material types. The net impact on the file size is insignificant so long as the number of material definitions is substantially less than the number of elements.
-
When generating tables of post-processing results with n88postfaim, results can be tabulated in subtables broken down by material ID. This is useful, but only so long as the number of defined materials stays within a range easily scanned by humans.
Although these are important advantages, there are occasions when the assumption of few material definitions is not so good. Here are two such cases:
| A |
A Homminga material table is used, which generates a sequence of varying material properties according to image density. In this case, we are typically talking about a material table of the order of one hundred material IDs. The assumptions 1 (solver pre-calculated values) and 2 (efficient file storage of material definitions) still hold, but the output of n88postfaim, if broken down by material, becomes cumbersome and excessive. |
| B |
Some researchers have proposed models in which the bone anisotropy is continuously variable. To model this with FE software requires that each element have its own stiffness matrix. Therefore the number of required material definitions is equal to the number of elements. In this case, following assumptions 1 and 2 results in a large inefficiencies: the solver uses greatly more memory, and the model file is many times larger than it would be for geometric data only. |
To address these issues, version 8 of Faim introduced the concept of material arrays, in contrast to the existing material tables. This is an expansion of the capabilities of Faim, and is really only relevant for the two cases listed above. For all other cases, one could say for normal usage, the previous concept of material tables is preferable, and it remains the default.
For the file format, a simple extension of the n88model standard is adopted,
wherein a material definition object within the file (in practice a group in netCDF terminology),
may optionally, instead of having named attributes, have
arrays of any length with the same names (where arrays in netCDF are called
variables). The length of the array indicates then that M materials are
being defined at once, and that they should get sequential material IDs.
Here are how the two above cases can be handled:
| A |
Homminga material table: You could have in your model file a single material
array of
length 127 for example. It has material ID 1, which implies the definition
of materials 1..127. The material ID for each of your elements is in this range.
This is in fact the method of operation of |
| B |
Continuously variable anisotropy: You could have in your model file a single material array of length equal to the number of elements N. It has material ID 1, implying the definition of materials 1..N . Consequently, you must have labelled your elements with sequential material IDs 1..N . |
These are the typical cases, but more exotic combinations are allowed. You don’t need to necessarily start an array at material ID 1, and you may define multiple material arrays. You can also mix traditional single material definitions with material arrays, and there is no requirement that all the definitions in your file are of the same type. For example, you could have one material array of isotropic materials, and another of orthotropic materials. The only rule is that be no overlap of material IDs, but otherwise in principle anything is allowed.
Let us look at the consequences for the solver.
For linear models, there are two solvers. The traditional and commonly used
solver n88solver_slt, which uses material tables internally, and the
new solver n88solver_sla, which uses material arrays internally, and is
efficient only when the number of material definitions is equal to or
comparable to the number of materials. Firstly, the solvers are entirely
independent of the n88model file. This is an important point:
all solvers can read all model files. n88solver_slt always converts
all material definitions in the model file, regardless of whether defined
individually
or in arrays, into a material table with entries for each material ID. This material table includes
pre-calculated local stiffness matrices, and the number of entries is equal to the
summed lengths of all defined material arrays, plus the number of
individually defined materials.
Conversely, n88solver_sla always generates an internal material
array of the same length as the number of elements. Even if you only define
one, or few, materials, these few materials will repeat over and over
so that there is one entry per element.
The critical efficiency of n88solver_sla as compared with n88solver_slt
is that only the minimal number of material parameters is stored in
the material array, and storage of pre-calculated values is avoied.
As a consequence
n88solver_sla is almost always slower than n88solver_slt; the trade-off
is that n88solver_slt uses really huge amounts of memory when
the number of defined materials becomes comparable to the number of
elements.
|
|
The script faim will always use the solver n88solver_slt except
in the single case where exactly one material array is defined,
and it has length equal to the number of elements. In this case,
faim will chose to use the n88solver_sla solver. You can
of course always run the solver of your choice manually.
|
Finally, when it comes to post-processing with n88postfaim, where sub-tables for each material ID are generated, all material IDs corresponding to a material array are grouped into a single subtable. This prevents the amount of output from becoming excessive.
8.2. Direct Mechanics
Microstructural organization plays an important role in macroscopic mechanical behaviour. For example, bone microarchitectural organization, as shown here in a human proximal femur, can exhibit patterns that are related to the macrostructural mechanical behaviour, and those patterns vary depending on the mechanical requirements at each location within the bone. A useful approach to characterizing the microstructural patterns (also referred to as “fabric”) is to determine the anisotropic properties of sub-volumes of bone. In some regions of the femur, for example, the bone microarchitecture will be highly aligned with the bone axis, but in other parts the alignment may be predominantly in a transverse orientation. The anisotropic properties typically need to be defined at several locations due to spatial variation.
Anisotropy can be defined in terms of either the fabric or mechanical behaviour. Methods for characterizing the fabric are based on techniques such as mean intercept length or star volume analysis, and a good resource is the paper by Odgaard (1997a). Essentially, fabric methods focus on the distribution of tissue microarchitecture. Alternatively, the mechanical elastic behaviour can be determined, and has been shown by Odgaard et al. (1997b) that the anisotropic fabric and mechanical properties are similar. This observation makes sense, and reinforces the concept that underlying bone micro-architecture is an important factor in determining mechanical behaviour. Here we focus on the determination of bone anisotropic elastic behaviour using a so-called direct mechanics assessment as proposed by van Rietbergen et al. (1996). In summary, six elastic finite element tests are performed on a cubic subvolume, and those results are used to define a 6×6 stiffness matrix that relates stress to strain as per Hooke’s Law,
The most general anisotropic material requires 21 independent coefficients to fully characterize, but it is usually most convenient to assume there are planes of elastic symmetry, in which case there exists an orientation of a coordinate system where only 9 independent elastic coefficients are needed. See the section Linear Orthotropic Material. In this case,
Finite element models of real measurement data of biological materials do not exhibit perfect orthotropic symmetry, therefore the process of reducing the 6×6 matrix from 21 independent coefficients to 9 involves finding an optimal coordinate system such that some of the coefficients are close to zero. It is reasonable to assume that bone mechanical behaviour can be reduced to a case of orthotropy; however, caution should be exercised as it is up to the user to determine whether this simplification is appropriate.
The basis of the direct mechanics approach is the application of six finite element tests to an appropriate bone subvolume:
-
uniaxial normal strain in the x-direction (εxx)
-
uniaxial normal strain in the y-direction (εyy)
-
uniaxial normal strain in the z-direction (εzz)
-
uniaxial shear strain in the x-direction (γyz)
-
uniaxial shear strain in the y-direction (γzx)
-
uniaxial shear strain in the z-direction (γxy)
These tests are applied under the conditions of unit engineering strain. Each test is evaluated for the six resulting stresses (σxx, σyy, σxx, σyz, σzx, σxy), thus providing directly the values of the 6×6 stiffness matrix. The stresses are calculated as a volume average, which can be shown to be equivalent to the surface stresses on the faces of the cube.
Finding the optimal rotation of the coordinate system to represent orthotropic behaviour involves first decomposing the stiffness matrix into symmetric and asymmetric components. The asymmetric component is discarded, as conservation laws require that the stiffness matrix be symmetric. (The asymmetric component thus consists entirely of measurement error.) An optimal rotation is then found that minimizes the coefficients that would be zero for a true orthotropic material expressed in the coordinate system of its planes of symmetry.
The primary outputs from the direct mechanics approach are the stiffness and compliance matrices (S = C-1) in the original coordinate system, as well as in the coordinate system of optimal orthotropy. The 3×3 rotation matrix R that describes the transformation from the specimen coordinate system to the optimal coordinate system is given; the rows are the principal axes in the original coordinate system. Finally, from the compliance matrix, the standard orthotropic elastic constants Ei,νij,Gii are extracted. See Linear Orthotropic Material for the definitions.
The use of the n88directmechanics tool is described in detail in n88directmechanics.
An example run of the direct mechanics analysis is shown below.
$ n88directmechanics test25a.aim
n88directmechanics version 6.0
Copyright (c) 2012, Numerics88 Solutions Ltd.
input_file = test25a.aim
material_table = homogeneous
youngs_modulus = 6829.0
poissons_ratio = 0.3
connectivity_filter = on
0.00 Reading image file test25a.aim
0.00 Read 17576 points from image file.
0.00 Applying connectivity filter.
0.00 Masked out 0 unconnected voxels.
0.00 Converting to hexahedral cells.
0.01 Generated 7087 hexahedrons
0.01 Creating material table.
0.01 Creating three uniaxial models.
0.03 Writing n88 model file: test25a_strain_xx.n88model
0.14 Writing n88 model file: test25a_strain_yy.n88model
0.25 Writing n88 model file: test25a_strain_zz.n88model
0.34 Creating three symshear models.
0.35 Writing n88 model file: test25a_strain_yz.n88model
0.46 Writing n88 model file: test25a_strain_zx.n88model
0.57 Writing n88 model file: test25a_strain_xy.n88model
0.66 Calling solver on test25a_strain_xx.n88model
2.20 Calling solver on test25a_strain_yy.n88model
3.76 Calling solver on test25a_strain_zz.n88model
5.23 Calling solver on test25a_strain_yz.n88model
6.59 Calling solver on test25a_strain_zx.n88model
7.87 Calling solver on test25a_strain_xy.n88model
9.05 Reading n88 model file: test25a_strain_xx.n88model
9.07 Reading n88 model file: test25a_strain_yy.n88model
9.08 Reading n88 model file: test25a_strain_zz.n88model
9.09 Reading n88 model file: test25a_strain_yz.n88model
9.10 Reading n88 model file: test25a_strain_zx.n88model
9.11 Reading n88 model file: test25a_strain_xy.n88model
Volume fraction = 0.45357
Apparent stiffness matrix in specimen coordinate system
[[ 1571.653 540.033 513.822 7.53 -121.22 -57.959]
[ 540.033 2029.046 469.974 78.591 -53.69 -50.673]
[ 513.822 469.974 1803.998 20.377 -57.014 -15.761]
[ 7.53 78.591 20.377 734.405 -23.127 -36.557]
[ -121.22 -53.69 -57.014 -23.127 627.396 13.969]
[ -57.959 -50.673 -15.761 -36.557 13.969 745.749]]
Apparent compliance matrix in specimen coordinate system
[[ 7.570e-04 -1.586e-04 -1.704e-04 1.977e-05 1.170e-04 4.323e-05]
[ -1.586e-04 5.610e-04 -1.000e-04 -5.441e-05 5.808e-06 2.090e-05]
[ -1.704e-04 -1.000e-04 6.294e-04 -4.883e-06 1.569e-05 -7.273e-06]
[ 1.977e-05 -5.441e-05 -4.883e-06 1.372e-03 4.787e-05 6.410e-05]
[ 1.170e-04 5.808e-06 1.569e-05 4.787e-05 1.621e-03 -1.819e-05]
[ 4.323e-05 2.090e-05 -7.273e-06 6.410e-05 -1.819e-05 1.349e-03]]
Material parameters in specimen coordinate system
-------------------------------------------
Exx = 1320.98
Eyy = 1782.54
Ezz = 1588.79
Gyz = 728.81
Gzx = 617.06
Gxy = 741.27
-------------------------------------------
nu_yx = 0.28270
nu_zx = 0.27081
nu_xy = 0.20950
nu_zy = 0.15888
nu_xz = 0.22516
nu_yz = 0.17825
-------------------------------------------
Optimum rotation matrix R:
[[ 0.32957 -0.83991 -0.4312 ]
[ 0.30346 0.52671 -0.79403]
[ 0.89404 0.13084 0.42846]]
Apparent stiffness matrix in best orthotropic coordinate system
[[ 2197.117 466.121 496.104 30.725 39.277 6.441]
[ 466.121 1852.499 506.856 32.259 14.028 -0.103]
[ 496.104 506.856 1464.576 -5.755 -28.362 14.264]
[ 30.725 32.259 -5.755 650.075 -35.665 -15.051]
[ 39.277 14.028 -28.362 -35.665 697.661 8.234]
[ 6.441 -0.103 14.264 -15.051 8.234 705.066]]
Apparent compliance matrix in best orthotropic coordinate system
[[ 5.068e-04 -8.804e-05 -1.419e-04 -2.273e-05 -3.367e-05 -1.863e-06]
[ -8.804e-05 6.126e-04 -1.826e-04 -2.865e-05 -1.630e-05 4.167e-06]
[ -1.419e-04 -1.826e-04 7.952e-04 2.496e-05 4.544e-05 -1.482e-05]
[ -2.273e-05 -2.865e-05 2.496e-05 1.546e-03 8.154e-05 3.175e-05]
[ -3.367e-05 -1.630e-05 4.544e-05 8.154e-05 1.442e-03 -1.571e-05]
[ -1.863e-06 4.167e-06 -1.482e-05 3.175e-05 -1.571e-05 1.419e-03]]
Material parameters in best orthotropic coordinate system
-------------------------------------------
Exx = 1973.20
Eyy = 1632.50
Ezz = 1257.55
Gyz = 646.74
Gzx = 693.58
Gxy = 704.48
-------------------------------------------
nu_yx = 0.14372
nu_zx = 0.17848
nu_xy = 0.17371
nu_zy = 0.22968
nu_xz = 0.28004
nu_yz = 0.29816
-------------------------------------------
9.47 Done.
8.3. Pistoia Failure Load Estimate
The failure load for a linear elastic model is based on the work by Dr. Walter Pistoia (Pistoia 2001a and 2001b). Numerics88 provides a tool, n88pistoia that can be used to carry out these calculations. In general, it is more accurate and preferable to solve an elastoplastic model in order to obtain failure loads. However, we include the Pistoia tool, mostly for those who wish to compare current data to older results on which a Pistoia analysis was done.
The basic principal is that failure load is defined as the load at which a pre-defined volume of tissue (percentage critical volume) exceeds a pre-defined Energy Equivalent Strain (critical EES). Typical values are 2.0% and 0.007, respectively. It should be noted that the so-called Pistoia criterion is not a standard failure criteria used in classical mechanics of materials; however, it has been extensively validated with experimental testing of cadaver bones, and it is the most widely used and accepted criterion for image-based linear FE modelling.
The first sub-table contains the failure load information (the sub-table is
denoted by a series of horizontal dots). The calculation of the failure load
requires post-processing the EES for each element of the solved linear FE
model. After ordering the EES in a histogram, the actual strain at the
critical volume threshold (e.g., 2%) is determined and reported in the table
as EES at vol_crit. As this is a linear FE model, a scale-factor for this
EES can be determined relative to the critical EES, and this is captured in
a defined factor. A table of factors is provided at the bottom of the Pistoia Failure Load Estimate table, and the
factor associated with the defined critical volume and critical EES is
reported specifically in this first sub-table (other values of critical volume
and critical EES could be applied if necessary using the alternative table
factors). Knowing the total reaction force of the solved model (usually RFz) and the
actual EES value at the critical volume, a linear factor can be applied to
estimate the failure load: failure load = RFz × factor .
|
|
Although a similar process can be applied to determine the torsional failure load (and is reported as torsional failure load) there have not been any experimental validations of this technique published to date. It is not recommended to use the reported torsional failure load until experimental validation is completed. Nevertheless, it is provided here for the users’ convenience. |
The second sub-table contains a summary of the axial and torsional stiffness
values, and these are identical to the previous corresponding tables. For
example, RFz from node set 1 has already been reported in
Nodal Forces as total F_z_. They are reported
again in this table for convenience.
|
|
All failure loads are calculated assuming that
axial compression or torsion was applied along the z-axis in the Data Frame.
|
The third sub-table contains a summary of the histogram results for the
analysis of EES. All materials defined in the model are pooled for this
histogram (i.e., cortical bone and trabecular bone), and it is the basis for
determining the EES at the critical volume used for the failure load
calculation. It is important to note that the user has the option to
pre-define a material that is to be excluded from the failure load analysis,
and that excluded material is reported at the top of the table (Excluded
material id). This is useful, for example, if the FE model contains platens
that should not be included in the failure load analysis (i.e., the failure
load of the platens are not of interest).
The fourth sub-table contains a summary of the number of elements that exceed critical EES, and is broken down by material definition. This information allows the user to determine, for example, whether failure was based on cortical bone versus trabecular bone.
The fifth sub-table contains factors that could be used (by user hand calculation) to determine the estimated failure load for different critical volumes or critical EES.
Table 1: Pistoia Failure Load Estimate ----------------------------------------------------------- Pistoia Criterion for Energy-Equivalent-Strain (EES) (*) Results valid for linear, isotropic model only. (*) Warning: Torsion failure load not validated. Caution! ----------------------------------------------------------- Number of elements in analysis: 349829 Excluded material id: none ........................................................... Critical volume (%): 2.0000 Critical EES: 0.0070 EES at vol_crit: 0.0131 Factor (from table): 0.5332E+00 Failure load (RFz * factor) [N]: -0.3248E+04Torsional failure load (Tz * factor) [Nmm]: 0.9764E-03 ----------------------------------------------------------- Axial and Torsional Stiffness: ........................................................... RFz (node set 1) [N]: -0.6091E+04 Uz (node set 1) [mm]: -0.9020E-01 Axial stiffness [N/mm]: 0.6753E+05
Tz (node set 1) [Nmm]: 0.1831E-02 Rotz (node set 1) [rad]: -0.1787E-03 Torsional stiffness [Nmm/rad]: -0.1025E+02
----------------------------------------------------------- Distribution of energy-equivalent-strain: EES = sqrt(2U/E). ........................................................... EES average 0.6135E-02 std_dev 0.3210E-02 minimum 0.1332E-07 maximum 0.3725E-01 skewness 0.4787E+00 kurtosis 0.9386E+00 median 0.6089E-02 ----------------------------------------------------------- Distribution of failed materials. ........................................................... material # els % 127 1454 20.7803 100 5543 79.2197
---------- ---------- ---------- total 6997 100.0000 ----------------------------------------------------------- Factor table: crit_vol | crit_ees % # vox | 0.0050 0.0060 0.0070 0.0080 0.0090 ------ -------- | ---------- ---------- ---------- ---------- ---------- 1.00 349829 | 0.3400E+00 0.4080E+00 0.4759E+00 0.5439E+00 0.6119E+00 2.00 699658 | 0.3809E+00 0.4570E+00 0.5332E+00 0.6094E+00 0.6855E+00 3.00 1049487 | 0.4071E+00 0.4886E+00 0.5700E+00 0.6514E+00 0.7329E+00 4.00 1399316 | 0.4274E+00 0.5129E+00 0.5984E+00 0.6838E+00 0.7693E+00 5.00 1749145 | 0.4444E+00 0.5333E+00 0.6222E+00 0.7111E+00 0.8000E+00 6.00 2098974 | 0.4582E+00 0.5498E+00 0.6414E+00 0.7331E+00 0.8247E+00 7.00 2448803 | 0.4703E+00 0.5644E+00 0.6585E+00 0.7525E+00 0.8466E+00
| Estimated failure load of the bone in uniaxial compression, given the critical volume of 2% and critical EES of 0.0070. | |
| Calculated based on the total Fz (also termed RFz) of node set 1 divided by the average displacement Uz of the surface defined by node set 1. | |
| Calculated based on the total Tz of node set 1 divided by the average displacement Uz of the surface defined by node set 1. | |
| Indicates that approximately 79% of the failed voxels comprising the 2% critical volume were in the trabecular tissue, while only 21% were in the cortical tissue. |
9. Command Reference
| Module | Description |
|---|---|
Convenience utility that calls n88solver, n88derivedfields and n88postfaim in sequence. |
|
Reduce the size of finite element models so that an approximate solution can be obtained quicker and with less memory. |
|
Copy, convert or compress a finite element model file. |
|
Compress a finite element model file in-place. |
|
Calculate additional field values (forces, stress, strain, etc) that are not generated by n88solver. |
|
Perform direct mechanics calculations. |
|
Calculate some values that indicate the correctness of the solution. |
|
Extracts specified solution fields as tabular text data. |
|
Extract node sets, element sets and constraint sets and write them to VTK
PolyData ( |
|
Copies and interpolates a solution from a solved reduced-resolution n88model file, produced using n88coarsen, into the original n88model file. |
|
Generate a finite element model from a segmented 3D image. |
|
Print summary information for a Numerics88 FE model file. |
|
Estimate failure loads from a linear model. |
|
Generate tables of standard post-processing quantities. |
|
Solvers suitable for small-strain models with linear elastic material definitions (_el) or with non-linear elastoplastic material definitions (_ep). |
|
Tabulate values from n88postfaim output files for importing into a spreadsheet. |
9.1. faim
A convenience utility that calls n88solver, n88derivedfields and n88postfaim in sequence on the specified model file.
The analysis file produced by n88postfaim will be named after the input file, with "_analysis.txt" replacing the extension of the input file.
The most appropriate solver for your input model will be used.
-
If your model contains elastoplastic material definitions,
n88solver_sptwill be used. -
If your model contains exactly one material array with length equal to the number of elements,
n88solver_slawill be used. -
In all other cases,
n88solver_sltwill be used.
The analysis file produced by n88postfaim will be named after the input file, with “_analysis.txt” replacing the extension of the input file.
The command line arguments of faim are listed below. As they are passed through to the programs doing the work, they are grouped by program that they are passed to. In each case the options are identical to those of the program doing the work.
convergence_measure convergence_tolerance device engine license_check maximum_iterations maximum_plastic_iterations quiet restart threads threshold_window plastic_threshold_window
For details, refer to n88solver.
device engine quiet threads
For details, refer to n88derivedfields.
element_sets node_sets quiet rotation_center
For details, refer to n88postfaim.
| Option | Description |
|---|---|
-h, --help |
Show help and exit. |
--use_coarsen |
Generate a coarsened model if possible to calculate an initial estimate of the solution. For certain models, this may speed-up finding the final solution. |
--no_post |
Do not run the postprocessor. |
9.2. n88coarsen
This tool is used to reduce the size of finite element models so that an approximate solution can be obtained quickly and with less memory. It operates either directly on FE models, or on segmented image data.
n88coarsen [-h] [--material_averaging {linear,homminga_density}]
input_file output_file
When operating on n88model files, it will increase the size of elements by a factor of 2 in each dimension (thus a factor of 8 in volume), resulting in fewer larger elements. The output model is coarser: the coarsening is always done by adding volume to make larger elements, never by removing material, so that as compared with the input model, the output model always has greater or equal volume. Material properties are averaged over all the input elements corresponding to each output element. Empty space is treated as having identically zero stiffness, wherever empty space in the input is encompassed within an output element. All essential features of the model, including boundary conditions, applied forces, and post-processing sets, are translated to the new coarser mesh.
When the input is an image, the resolution is reduced by exactly 1/2 in each
linear dimension. Each 2x2x2 cube in the input becomes a single voxel in the
output, with value equal to the maximum in the corresponding input 2x2x2.
This operation does not average input values, since it does not make any
sense to average segmentation values, which are just labels. Instead, it
takes the maximum value over all the input voxels corresponding to an output
voxel. This is a somewhat arbitrary choice. For this reason it is preferable
to use n88coarsen directly on n88model files, where material averaging is
possible.
-
Numerics88 model file (.n88model)
-
DICOM (a directory)
-
Scanco AIM (.aim)
-
MetaImage (.mha or .mhd)
-
VTK XML ImageData (.vti)
-
Numerics88 model file (.n88model). If the input is an n88model file.
-
VTK XML ImageData (.vti). If the input is an image.
| Option | Description |
|---|---|
-h, --help |
Show help and exit. |
--material_averaging |
Determine how the material averaging is done. If
|
9.3. n88copymodel
Copy, convert or compress a finite element model file.
n88copymodel [-h] [--compress] input [input2] output
File formats are automatically identified by their extensions. Ambiguous input file extensions are resolved by examining the file.
Two input files are allowed if the first is a FAIM version 5 input file (.inp),
and the second is a FAIM version 5 output file (.dat). This will create
a complete, solved n88model file. Either .inp or .dat can also be converted individually,
but in the case of .dat files, the resulting n88model file will be incomplete,
as the .dat file alone does not contain either material definitions or
constraints; however, it can be rendered and processed by n88postfaim, but not re-solved.
-
Numerics88 model file (.n88model)
-
Abaqus input file (.inp)
-
Faim version 5 input file (.inp)
-
Faim version 5 output file (.dat)
-
Numerics88 model file (.n88model)
-
Abaqus input file (.inp)
-
VTK XML Unstructured Grid file (.vtu)
|
|
VTK XML Unstructured Grid files can be read be and rendered by ParaView, even without the Numerics88 plugins. They include the complete geometry, plus any solution fields, but lack any constraint or material information. |
| Option | Description |
|---|---|
-h, --help |
Show help and exit. |
--compress, -c |
Use compression when writing the output file if the file
format supports it. Compressed |
|
|
If you compress an n88model file, and then run either n88solver
or n88derivedfields on it, it will end up in a mixed state, where the
original data is compressed, but the new data added by n88solver
or n88derivedfields is uncompressed. There is nothing wrong with this as
the file is still completely valid and useable. However, usually if
compression is important, one wants the entire file data compressed.
Therefore, we recommend not compressing the file until you have completed
all the normal processing steps on it. It is of course possible to
convert a partially compressed n88model file to a fully compressed
n88model file by running n88copymodel or n88compress on it again.
|
See also the section Converting Faim version 5 file formats.
9.4. n88compress
n88compress FILENAME
is an alias for
n88copymodel --compress FILENAME FILENAME
Refer to the documentation for n88copymodel.
9.5. n88derivedfields
Calculates additional field values (forces, stress, strain, etc) that are not generated by n88solver.
For discussion of use, see the section on using n88derivedfields in the Post-processing chapter.
n88derivedfields [options] input_file
| Argument | Description |
|---|---|
--help [-h] |
Print help and exit. |
--version[-v] |
Print version information. |
--quiet [-q] |
Suppress output to terminal (except for error messages). |
--precision arg (=single) |
Set the floating point precision used. Values: single, mixed, double. |
9.6. n88directmechanics
Perform direct mechanics calculations. See Direct Mechanics in the Special Topics chapter.
n88directmechanics [-h] [-c FILE] [--generate] [--solve] [--analyze]
[--material_table {homogeneous,homminga}]
[--youngs_modulus YOUNGS_MODULUS]
[--poissons_ratio POISSONS_RATIO]
[--orthotropic_parameters ORTHOTROPIC_PARAMETERS]
[--homminga_maximum_material_id HOMMINGA_MAXIMUM_MATERIAL_ID]
[--homminga_modulus_exponent HOMMINGA_MODULUS_EXPONENT]
[--connectivity_filter {on,off}]
input_file
| Option | Description |
|---|---|
input_file |
An image file with segmented
data. Note
that the file name of the original image file should
be used even when the only action is - DICOM (a directory) - Scanco AIM (.aim) - MetaImage (.mha or .mhd) - VTK XML ImageData (.vti) |
| Option | Description |
|---|---|
--generate |
Generate models. (Generates 6 n88model files.) |
--solve |
Solve models. (n88model files are updated with solutions.) |
--analyze |
Perform direct mechanics analysis on solved files. |
Multiple action arguments may be specified. If no action argument is specified, it is equivalent to specifying them all.
material_table youngs_modulus poissons_ratio orthotropic_parameters homminga_maximum_material_id homminga_modulus_exponent
These arguments are identical to the equivalent arguments of n88modelgenerator. See Material specification parameters.
| Option | Description |
|---|---|
-h, --help |
Show help and exit. |
-c FILE, --config FILE |
Specify a configuration file. The configuration file may specify any arguments that take a value, one per line, in the format name=value (leave the double dash "--" off of the argument name). This format is identical to n88modelgenerator. See Running n88modelgenerator. |
connectivity_filter spacing
These arguments are identical to the equivalent arguments of n88modelgenerator. See Input image parameters.
|
|
There are no options passed to the solver. If this is required, run
n88directmechanics with the --generate action, then manually run
n88solver on
each of the resulting n88model files, using the desired solver options, then
run n88directmechanics again with the --analyze action.
|
9.7. n88evaluate
A tool to evaluate the quality of solutions.
For discussion of use, see the section on using evaluating solution quality and the section section on using evaluating nonlinear solution quality.
n88evaluate [options] input_file
| Argument | Description |
|---|---|
--help [-h] |
Print help and exit. |
--sparse [-s] |
Use sparse matrices for calculation. This is the default, but requires that scipy be installed. |
--dense [-t] |
Use dense matrices for calculation. This does not require scipy to be installed, but as the memory requirements scale as the square of the number of degrees of freedom in the problem, this is feasible only for very small problems. |
9.8. n88extractfields
Extracts specified solution fields as tabular text data.
n88extractfields [-h] [--output_file OUTPUT_FILE] fields input_file
| Option | Description |
|---|---|
fields |
A comma-delimited list of names of solution fields to extract.
May be the name of either a solution node value (e.g.
“Displacement”) or a solution element value (e.g. “Stress”;
see also
Calculating additional solution fields with n88derivedfields)
Additionally, “NodeNumber”, “ElementNumber”, “MaterialID”, “NodeCoordinates”,
“ElementCoordinates” or “Topology” can be specified.
Element coordinates are the centers of the elements. Topology
gives for each element the 8 node numbers of the nodes
constituting the element. The order is as in the |
input |
The model file. |
| Option | Description |
|---|---|
-h, --help |
Show help and exit. |
--output_file OUTPUT_FILE, -o OUTPUT_FILE |
Output file. If not specified, output will go to STDOUT. |
This will extract the displacement values as an N×3 array, where N is the number of nodes:
$ n88extractfields Displacement mymodel.n88model -0.00136573 -0.00136573 0.0 -0.000770869 -0.00142601 0.0 -0.000218384 -0.00141035 0.0 0.000218384 -0.00141035 0.0 0.000770869 -0.00142601 0.0 0.00136573 -0.00136573 0.0 -0.00142601 -0.000770869 0.0 ...
This example will extract both element number and corresponding stress. As the stress is 6-valued, this makes a total of 7 values per row of output:
$ n88extractfields ElementNumber,Stress mymodel.n88model 1 -0.752387 -0.752387 -69.0185 0.965844 0.965844 -0.00933552 2 -4.98979 -1.50565 -73.2319 0.629349 0.690826 1.61737 3 -6.35569 -0.494144 -74.5778 0.486541 -4.27155e-16 -5.6954e-16 4 -4.98979 -1.50565 -73.2319 0.629349 -0.690826 -1.61737 5 -0.752385 -0.752386 -69.0185 0.965844 -0.965844 0.00933552 6 -1.50565 -4.98979 -73.2319 0.690826 0.629349 1.61737 7 -1.50565 -4.98979 -73.2319 0.690826 -0.62934 ...
9.9. n88extractsets
Extract node sets, element sets and constraint sets and write them to VTK PolyData (.vtp) files which can be opened with ParaView. This is mostly useful for visualizing sets, boundary conditions and applied forces. For nodes sets and constraints, these files will consist of a collection of vertices.
n88extractsets [-h] [--constraints] [--node_sets] [--element_sets] input
| Option | Description |
|---|---|
-h, --help |
show this help message and exit |
--constraints, -C |
Extract constraints. |
--node_sets, -N |
Extract node sets. |
--element_sets, -E |
Extract element sets. |
If no arguments are specified, all types of sets will be extracted.
|
|
This utility will generate file names based on the names of the sets, and will overwrite existing files with the same names without warning. |
9.10. n88interpolatesolution
Copies and interpolates a solution from a solved reduced-resolution n88model file, produced using n88coarsen, into the original n88model file. This may help to obtain faster solutions.
n88interpolatesolution [-h] full_model reduced_model
|
|
For linear models only. |
9.11. n88modelgenerator
Generates a finite element model from a segmented 3D image.
Refer to the chapter on using n88modelgenerator.
n88modelgenerator [options] input_file [output_file]
n88modelgenerator currently supports the following input formats:
-
DICOM (automatically selected when a directory is given as the input),
-
Scanco
.aimfiles, -
ITK MetaImage files (
.mha) or (.mhd), -
VTK XML Image Data files (
.vti), -
existing Numerics88 Model file (
.n88model)
|
|
There are some limitations when reading DICOM files. In particular, encapsulated format cannot be read. It is sometimes not possible to determine the z-spacing from DICOM files. In this case use the option spacing. |
|
|
If an n88model file is provided as an input file, the mesh (i.e. the points and elements) will be taken from the input, as well as any possible solution fields. A new material table and new constraints will be generated. This is useful for incremental loading tests of nonlinear models, as it allows the boundary conditions to be updated while preserving an existing solution. |
The standard output format of n88modelgenerator is an n88model file
(see n88model File Format). If you specify an output file with
extension .n88model, the n88model file format will be used. This
is the default output type, and if no output file is specified, an
output file will be generated from the stem of the input file, with the
extension .n88model appended.
n88modelgenerator also supports the output of Abaqus input files.
An Abaqus input file will be generated whenever an output file with
extension .inp is specified.
Input and output parameters specify the files that are used for input and output.
| Argument | Description |
|---|---|
Specify the name of the input file. Note that it is not necessary to explicitly use “--input_file” on the command line, as the first positional argument (i.e. the first argument not starting with a dash), is taken to be the input file. |
|
Specify the name of the output file. If not specified, a default
output file name will be used, which is of the form
|
| Argument | Description |
|---|---|
Force the spacing of the input image. This
is sometimes required for DICOM files, for
which the z-spacing sometimes cannot be
determined. Values should be given as a
comma-delimited list of x,y,z values. e.g. |
|
Enable/disable connectivity filtering which extracts
only the largest connected object in the input image. See
Ensuring connectivity in the chapter about |
Test configuration parameters define the mechanical test that will be applied to the object in the image.
| Argument | Description |
|---|---|
Specify test type. Valid values are |
|
Specify the test axis. See Test Orientation. Valid values are x, y, and z. The default is z. |
|
For a compression type test, specifies an apparent level strain. Negative values correspond to compression. Strain is the default if neither strain nor displacement are specified. Default -0.01, corresponding to 1% compressive strain. |
|
For a symshear test, this sets the apparent engineering shear strain applied to the model. Unitless. Default 0.01. |
|
strain |
Shortened equivalent of either normal_strain or shear_strain, depending on the test type. |
Specify an applied displacement (with units of length) for a compression type test.
Negative values correspond to compression.
This parameter is exclusive with |
|
Fully define the constraints for a uniaxial model by adding an arbitrary
pinned point to prevent lateral translation, and a second partially
pinned point to prevent lateral rotation. If this option is off, the
system of equations for a uniaxial test is singular. Faim can solve it
regardless, and will in fact typically solve it faster. This option is
ignored for test types other than uniaxial.
Valid values are |
|
The x,y coordinates (in the Test Frame) of the central axis,
which is parallel to the z axis (in the Test Frame).
Example: |
|
The degree of tilt between the top and bottom surfaces in a bending test. Units are degrees. The default is 1º. |
|
The angle of the neutral axis in the x,y plane (in the Test Frame) in a bending test. 0º is parallel to the x-axis. Units are degrees. Default is 90º, parallel to the y-axis. |
|
The amount of shear displacement of the top surface as a vector in the x,y plane (in the Test Frame) for a dshear test. Units are length units if scale_shear_to_height is off, otherwise a unitless ratio. Default is 0.01,0 . |
|
If |
|
Amount of rotation of the top surface in a torsion test. Units are degrees. Default is 1º. |
Surface detection parameters modify how the top and bottom surfaces of the object image are identified. For most test types, the principle boundary conditions are applied to these two surfaces. If not specified, by default these surfaces are identified as all nodes (or elements) at the top or bottom extent of the input.
| Argument | Description |
|---|---|
Specify method of selecting top surface. Valid values are |
|
Specify method of selecting bottom
surface. Valid values are |
|
Specify the maximum depth for identifying the top surface. Only applies
if |
|
Specify the maximum depth for identifying the bottom surface. Only applies
if |
|
Apply boundary conditions at the top surface only to cells and nodes of the specified material ID. |
|
Apply boundary conditions at the bottom surface only to cells and nodes of the specified material ID. |
Material specification parameters are used to specify material definitions, and to select a material table that maps material IDs to material definitions.
| Argument | Description |
|---|---|
Specify isotropic Poisson’s ratio. The default is 0.3 . |
|
Specify isotropic Young’s modulus. The default is 6829. |
|
Specify orthotropic parameters as
Ex,Ey,Ez,νyz,νzx,νxy,Gyz,Gzx,Gxy .
If not set, isotropic parameters will be assumed.
Important: There are two common conventions for ordering the mixed index
quantities νij and Gij. Numerics88 software uses the ordering YZ,
ZX, XY. It is important to observe this when specifying orthotropic
properties in |
|
Specify an elastoplastic yield criterion. Specify as several values separated by commas. The first value is an elastoplastic yield criterion name; subsequent values are numeric arguments appropriate to the method. Supported methods: |
|
Specify method for generating material table.
Valid values are |
|
Specify the maximum material ID used in Homminga density to modulus conversion. The default is 127. |
|
Specify exponent used in Homminga density to modulus conversion. The default is 1.7 . |
|
Specify a material definitions file for advanced material specification. If specified, all other material specification arguments will be ignored. Refer to the section material definitions file in the chapter on Preparing Finite Element Models With n88modelgenerator. |
Solver parameters affect the execution of the solver. They are independent
of the model creation, and are specific to the solver used. If given
as arguments to n88modelgenerator, they will be stored in the n88model
file. However for most purposes, it is better to leave these out of the
n88model file and either use the defaults as selected by the solver,
or else to specify them as command line arguments directly to the solver. See
n88solver.
| Argument | Description |
|---|---|
Specify convergence tolerance for conjugate gradient iterations. If not specified a default value will be used. See Generating the displacements with n88solver. |
|
Specify the maximum number of conjugate gradient iterations. If not specified a default value will be used. The default is 30000. See Generating the displacements with n88solver. |
|
Specify convergence tolerance for plastic iterations. If not specified a default value will be used. |
|
Specify the maximum number of plastic iterations. If not specified a default value will be used. The default is 100. |
9.12. n88modelinfo
Print summary information for a Numerics88 finite element model file.
n88modelinfo [-h] [--active] [--history] [--log] [--materials]
[--parts] [--node_sets] [--element_sets] [--sets]
[--constraints] [--problems] [--solutions]
input_file
| Option | Description |
|---|---|
input_file |
The .n88model file to read. |
| Option | Description |
|---|---|
--active |
List active solution, problem and part. |
--history |
Show history. |
--log |
Show log. |
--materials |
List defined materials. |
--parts |
Show parts. |
--node_sets |
Show nodesets. |
--element_sets |
Show elementsets. |
--sets |
Show both node and element sets. (Equivalent to --node_sets and --element_sets.) |
--constraints |
Show constraints. |
--problems |
Show problems. |
--solutions |
Show solutions. |
Multiple action arguments may be specified. If no action argument is specified, it is equivalent to specifying them all.
| Option | Description |
|---|---|
-h, --help |
Show help and exit. |
9.13. n88pistoia
Calculate Pistoia yield critera. This is a method if estimating yield strength from linear solutions. In general, it would be preferable to use a non-linear elastoplastic model to calculate yield strengths. This utility is provided mostly for comparing with older results.
For discussion of use, see the section on the Pistoia failure load estimate in the special topics chapter.
Note that n88pistoia is implemented in python (in tools/pistoia.py), so you
can copy it and modify it should you wish to modify the analysis.
n88pistoia [options] input_file
| Argument | Description |
|---|---|
--help [-h] |
Print help and exit. |
--output_file [-o] arg |
Specify an output file. If no output file is specified, output will go to STDOUT. |
--constraint [-n] arg |
Specify the constraint (i.e. boundary condition or applied load) to use for analysis. This is the surface to which forces are applied. The default ("top_displacement") will work for models generated with n88modelgenerator. |
--rotation_center [-c] arg |
Specify the spatial center used for calculation of angular quantities. The argument must be given as a triplet of coordinates. If not specified, the value will be read from the input file. If not available, no angular quantities will be calculated. |
--include [-i] arg |
Only elements with the specified material IDs will be included in the calculation. Multiple IDs can be specified in a comma-delimited list (e.g. 100,101,105). |
--exclude [-e] arg |
All elements with the specified material IDs will be excluded from the calculation. Multiple IDs can be specified in a comma-delimited list (e.g. 100,101,105). |
--critical_volume arg |
Specify the fixed critical volume (as percent) (e.g. 2.0). |
--critical_strain arg |
Specify the fixed critical strain (e.g. 0.007). |
9.14. n88postfaim
Generate tables of standard post-processing quantities.
For discussion of use, see the section on using n88postfaim in the post-processing chapter.
Note that n88postfaim is implemented in python (in tools/postfaim.py), so you
can copy it and modify it should you wish to modify the analysis.
n88postfaim [options] input_file
| Argument | Description |
|---|---|
--help [-h] |
Print help and exit. |
--output_file [-o] arg |
Specify an output file. If no output file is specified, output will go to STDOUT. |
--node_sets [-N] arg |
Specify the node sets to use for analysis. The argument should be a list of node set names, separated by commas. If not specified, the value will be read from the input file. |
--element_sets [-E] arg |
Specify the element sets to use for analysis. The argument should be a list of element set names, separated by commas. Each node set must be matched by the corresponding set of elements. If not specified, the value will be read from the input file. |
--sets [-s] arg |
A convenience option that sets both node_sets and elements_sets. This is only useful if corresponding node and element sets are identically named. |
--rotation_center [-c] arg |
Specify the spatial center used for calculation of angular quantities. The argument must be given as a triplet of coordinates. If not specified, the value will be read from the input file. If not available, no angular quantities will be calculated. |
9.15. n88solver (_slt, _sla and _spt)
n88solver_slt and n88solver_sla are solvers suitable for small-strain models
with linear elastic material definitions. n88solver_spt can solve nonlinear models
containing elastoplastic material definitions.
n88solver_slt and n88solver_spt use material tables internally: they are most
efficient when the number of defined materials is substantially less than
the number of elements in the model. This is the usual case. n88solver_sla
is a special-purpose solver that uses a material array internally: it is more
efficient when the number of defined materials is comparable to the number
of elements. See
Efficient Handling of Large Numbers of Material Definitions.
See the chapters on Solving Linear Problems and Solving Nonlinear Problems for discussion of use.
n88solver_slt [options] input_file n88solver_sla [options] input_file n88solver_spt [options] input_file
| Argument | Description |
|---|---|
--help [-h] |
Print help and exit. |
--version [-v] |
Print version information and exit. |
--quiet [-q] |
Suppress output to terminal (except for error messages). |
--license-check [-l] |
Print licensing information. |
Set the solver engine. Valid values are
|
|
Set the number of threads for the mt engine. If not specified, the number of threads will be set to one per CPU core on the system, or one thread per 2048 elements, whichever is less. |
|
Set the nVidia CUDA device to use (applies only to nv solver). Multiple devices may be specified in a comma delimited list. |
|
--precision arg (=double) |
Set the floating point precision used.
Values: |
Do not use the existing solution as initial value. |
|
Set the convergence measure.
See convergence measure in the section on
solving linear models. For linear models, if |
|
Set the convergence tolerance. |
|
Set the linear convergence window. Convergence is not considered reached until the convergence measure remains below the threshold for at least this number of consecutive iterations. |
|
Set the plastic convergence window. Plastic convergence is not considered reached until the convergence measure remains below the threshold for at least this number of consecutive iterations. |
|
Set maximum number of linear iterations. Note that for elastoplastic models the count of linear iterations is reset on each plastic iteration. [-N] arg |
|
Set maximum number of plastic iterations. |
|
Specify a file to output all iteration data. |
The convergence_tolerance, maximum_iterations, and maximum_plastic_iterations
may also be set in the input file. If present in both the input
file as well as specified on the command line as options to n88solver,
the options on the command line to n88solver take precedence.
9.16. n88tabulate
Extract and tabulate values from n88postfaim output files. The result is suitable for importing into a spreadsheet.
n88tabulate [-h] [--variables VARIABLES] [--from FROM] [--header]
[--delimiter DELIMITER] [--output_file OUTPUT_FILE]
[input_files [input_files ...]]
| Option | Description |
|---|---|
input_files |
|
| Option | Description |
|---|---|
-h, --help |
show this help message and exit |
--variables VARIABLES, -V VARIABLES |
A list of the variables to extract from the input files. Separate variable names with commas. See below for a list of valid variable names. If not specified all possible variables will be selected (this makes for a very large table). |
--from FROM, -f FROM |
Obtain the list of variables from the first line of a
text file. The variable names may be separated by any
kind of delimiter (white space or commas). Note that
an output file (from n88tabulate, generated with the
|
--header, -H |
Print a header line first. May be used even if no input files are specified. |
--delimiter DELIMITER, -d DELIMITER |
Delimiter character to separate columns. Default is a tab (“\t”). |
--output_file OUTPUT_FILE, -o OUTPUT_FILE |
Output file. If not specified, output will go to STDOUT. |
For any variables not found in the analysis file, a dash (“-”) will be inserted into the output table.
In the following example, every possible variable will be extracted from
every file ending in “_analysis.txt” in the directory. This will result
in a very large number of values. The output will be written to the file
summary.txt.
n88tabulate -H -o summary.txt *_analysis.txt
In the following example, we request the total forces along the z direction on the first two node sets for two different analysis files.
$ n88tabulate -H -V "filename,fz_ns1,fz_ns2" test25a_analysis.txt test42a_analysis.txt filename fz_ns1 fz_ns2 test25a_uniaxial.n88model -0.1019E+02 0.1019E+02 test42a_uniaxial.n88model -0.4641E+02 0.4641E+02
The following example is exactly the same, but the output goes to a file.
n88tabulate -H -V "filename,fz_ns1,fz_ns2" -o summary.txt test25a_analysis.txt test42a_analysis.txt
Now suppose we want the same selection of variables on a different
analysis file, we could do the following. Notice that we are getting the
list of variables from the existing file summary.txt.
$ n88tabulate -H --from summary.txt test99a_analysis.txt filename fz_ns1 fz_ns2 test99a_uniaxial.n88model -0.6442E+02 0.6442E+02
In the following example, we are interested in the strain energy density, and request some statistical values. We also use a comma as the delimiter.
$ n88tabulate -H -d ',' -V "sed_avg,sed_stddev,sed_skew,sed_kurt" analysis.txt sed_avg,sed_stddev,sed_skew,sed_kurt 0.2990E+00,0.1127E+00,-0.1512E+01,0.8999E+00
In the variable list, certain variables can take one or more numeric indices.
This is denoted with %. For example, for id_mat%m, actual variable names
are id_mat1 for the first defined material, id_mat2 for the second
defined material, and so on. Similarly for dx_avg_ns%n, actual variables
names are dx_avg_ns1 for the first node set, dx_avg_ns2 for the second
node set, and so on.
| variable name | value in analysis file table |
|---|---|
filename |
Filename |
num_els |
Number of elements |
num_nodes |
Number of nodes |
Refer to Model Input.
| variable name | value in analysis file table |
|---|---|
mats_mats |
Number of materials |
id_mat%m |
The material ID of the mth defined material |
count_mat%m |
Number of elements for the mth defined material |
Refer to Materials.
| variable name | value in analysis file table |
|---|---|
num_pp_sets |
The number of sets used in post-processing. |
Refer to Post-processing sets.
| variable name | value in analysis file table |
|---|---|
sed_avg |
average (all materials) |
sed_stddev |
std_dev (all materials) |
sed_skew |
skewness (all materials) |
sed_kurt |
kurtosis (all materials) |
sed_min |
minimum (all materials) |
sed_max |
maximum (all materials) |
sed_median |
median (all materials) |
sed_avg_mat%m |
average over the mth defined material |
sed_stddev_mat%m |
sed_dev over the mth defined material |
sed_skew_mat%m |
skewness over the mth defined material |
sed_kurt_mat%m |
kurtosis over the mth defined material |
sed_min_mat%m |
minimum over the mth defined material |
sed_max_mat%m |
maximum over the mth defined material |
sed_median_mat%m |
median over the mth defined material |
Refer to Strain Energy Density.
| variable name | value in analysis file table |
|---|---|
svm_avg |
average (all materials) |
svm_stddev |
std_dev (all materials) |
svm_skew |
skewness (all materials) |
svm_kurt |
kurtosis (all materials) |
svm_min |
minimum (all materials) |
svm_max |
maximum (all materials) |
svm_median |
median (all materials) |
svm_avg_mat%m |
average over the mth defined material |
svm_stddev_mat%m |
svm_dev over the mth defined material |
svm_skew_mat%m |
skewness over the mth defined material |
svm_kurt_mat%m |
kurtosis over the mth defined material |
svm_min_mat%m |
minimum over the mth defined material |
svm_max_mat%m |
maximum over the mth defined material |
svm_median_mat%m |
median over the mth defined material |
Refer to Von Mises Stress.
| variable name | value in analysis file table |
|---|---|
dx_avg_ns%n |
The average displacement in the x direction over all nodes in the nth node set. |
dx_stddev_ns%n |
The standard deviation of the displacement in the x direction over all nodes in the nth node set. |
dx_min_ns%n |
The minimum displacement in the x direction over all nodes in the nth node set. |
dx_max_ns%n |
The maximum displacement in the x direction over all nodes in the nth node set. |
dx_median_ns%n |
The median displacement in the x direction over all nodes in the nth node set. |
dy_avg_ns%n |
The average displacement in the y direction over all nodes in the nth node set. |
dy_stddev_ns%n |
The standard deviation of the displacement in the y direction over all nodes in the nth node set. |
dy_min_ns%n |
The minimum displacement in the y direction over all nodes in the nth node set. |
dy_max_ns%n |
The maximum displacement in the y direction over all nodes in the nth node set. |
dy_median_ns%n |
The median displacement in the y direction over all nodes in the nth node set. |
dz_avg_ns%n |
The average displacement in the z direction over all nodes in the nth node set. |
dz_stddev_ns%n |
The standard deviation of the displacement in the z direction over all nodes in the nth node set. |
dz_min_ns%n |
The minimum displacement in the z direction over all nodes in the nth node set. |
dz_max_ns%n |
The maximum displacement in the z direction over all nodes in the nth node set. |
dz_median_ns%n |
The median displacement in the z direction over all nodes in the nth node set. |
Refer to Nodal Displacements.
| variable name | value in analysis file table |
|---|---|
fx_ns%n |
The total force in the x direction over all nodes in the nth node set. |
fx_stddev_ns%n |
The standard deviation of the force in the x direction over all nodes in the nth node set. |
fx_min_ns%n |
The minimum force in the x direction over all nodes in the nth node set. |
fx_max_ns%n |
The maximum force in the x direction over all nodes in the nth node set. |
fx_median_ns%n |
The median force in the x direction over all nodes in the nth node set. |
fy_ns%n |
The total force in the y direction over all nodes in the nth node set. |
fy_stddev_ns%n |
The standard deviation of the force in the y direction over all nodes in the nth node set. |
fy_min_ns%n |
The minimum force in the y direction over all nodes in the nth node set. |
fy_max_ns%n |
The maximum force in the y direction over all nodes in the nth node set. |
fy_median_ns%n |
The median force in the y direction over all nodes in the nth node set. |
fz_ns%n |
The total force in the z direction over all nodes in the nth node set. |
fz_stddev_ns%n |
The standard deviation of the force in the z direction over all nodes in the nth node set. |
fz_min_ns%n |
The minimum force in the z direction over all nodes in the nth node set. |
fz_max_ns%n |
The maximum force in the z direction over all nodes in the nth node set. |
fz_median_ns%n |
The median force in the z direction over all nodes in the nth node set. |
Refer to Nodal Forces.
| variable name | value in analysis file table |
|---|---|
fx_ns%n_mat%m |
The force in the x direction over nodes in the nth node set, summed over nodes belonging to the mth defined material. |
fy_ns%n_mat%m |
The force in the y direction over nodes in the nth node set, summed over nodes belonging to the mth defined material. |
fz_ns%n_mat%m |
The force in the z direction over nodes in the nth node set, summed over nodes belonging to the mth defined material. |
Refer to Load Sharing.
| variable name | value in analysis file table |
|---|---|
pis_stiffx |
The stiffness in the x direction. |
pis_stiffy |
The stiffness in the y direction. |
pis_stiffz |
The stiffness in the z direction. |
pis_fx_fail |
The estimated failure load in the x direction. |
pis_fy_fail |
The estimated failure load in the y direction. |
pis_fz_fail |
The estimated failure load in the z direction. |
|
|
The Pistoia Failure Load Estimate table is no longer generated by n88postfaim, but may be generated by the tool n88pistoia if desired. The corresponding variables are by default not included, unless a variable list which includes them is specified. |
Refer to Pistoia Failure Load Estimate and n88pistoia.
Appendix A: Upgrading from previous versions
A.1. Upgrading from Faim version 7
A.1.1. Changing from vtkn88 to vtkbone
In version 8, the closed-source vtkn88 is replaced with the open-source vtkbone.
Therefore, in all your python scripts, you will have to search for vtkn88
and replace it with vtkbone. (Similarly for the capitalized versions: VTKN88 →
VTKBONE.)
A.2. Upgrading from Faim version 6
A.2.1. Updating version 6 vtkn88 scripts to work with version 7
vtkn88 is now based on VTK version 6. Many of the example scripts in vtkn88
version 6 and earlier used the VTK method SetInput, which has been deprecated and replaced with SetInputData. Simply replacing SetInput with SetInputData
is sufficient to fix these scripts.
For example, here is a simple operation, in Python, that writes a n88model file. This is the version 6 version:
writer = vtkn88.vtkn88N88ModelWriter() writer.SetInput(model) writer.SetFileName(output_file) writer.Update()
For version 7, it needs to be updated to:
writer = vtkn88.vtkn88N88ModelWriter() writer.SetInputData(model) writer.SetFileName(output_file) writer.Update()
A.3. Upgrading from Faim version 5
A.3.1. Converting Faim version 5 file formats
Faim version 5 used two file formats: .inp files for input files to faim,
and .dat files for output. These can be upgraded to version 6 style
n88model files with the n88copymodel tool. You may
want to upgrade old archived files. Besides being much more space efficient,
the new file format is also more robust. It is also standards-compliant,
and is more easily read with third party software. (See n88model File Format.)
To convert a version 5 style file, use n88copymodel like this,
n88copymodel olddata.inp newdata.n88model
You can also specify that compression be used in writing the n88model
file, like this
n88copymodel --compress olddata.inp newdata.n88model
Compressed n88model files take less disk space, but are slower to read
and particularly to write. They are otherwise identical to uncompressed
n88model files. You never need to uncompress them before using them.
Version 5 .dat output files are somewhat more problematic to convert
to version 6 n88model files, because the .dat files do not contain the
complete model information. In particular, they lack any information
about material parameters or about boundary conditions or applied loads.
Nevertheless, if you have only a .dat file, it is still possible to convert
it to a n88model file, but the resulting model will be incomplete. It can
be opened and visualized with ParaView, and it is possible to read the
solution fields out of it, but it cannot be re-solved, nor can it be processed
with n88postfaim.
A .dat file can be converted with
n88copymodel olddata.dat newdata.n88model
As before, you may optionally specify --compress.
If you have both the original .inp and the .dat file, they can be
converted to a single n88model file by specifying both as input arguments,
n88copymodel olddata.inp olddata.dat newdata.n88model
The order is important: the .inp should be specified first. |
This will create a n88model file that can used either as a complete input
file to n88solver, should you wish to solve it again, and that also
contains the complete solution fields.
A.3.2. Updating 5 vtkn88 scripts to work with 6
Here we outline the steps required to update a version 5.x vtkn88
script to work in 6.0 . We do not document all the changes and additions
to vtkn88 in 6.0, instead we only concentrate on those changes that must
be made to get old scripts to work correctly in 6.0
-
vtkn88Materialinstances should be assigned a name.
All materials are now required to have a unique name. In fact, if you
don’t explicitly set a name, vtkn88 will assign a unique name for you,
but it will be an uninformative name such as “NewMaterial1”. Names can
be assigned like this:
bone_material = vtkn88.vtkn88LinearIsotropicMaterial()
bone_material.SetName("bone")
-
Method
SetModelSourceDescriptionofvtkn88FiniteElementModelis deprecated.
Having this method present will not prevent the scripts from running, but
will generate a warning message. The functionality is now encompassed
by the Log field of vtkn88FiniteElementModel , which allows
a much greater amount of information to be recorded.
-
Method
NodeIdsFromSelectionofvtkn88FiniteElementModelis deprecated.
Use the method GetNodeSet instead.
-
Method
CreateDisplacementConstraintofvtkn88FiniteElementModelis renamed toApplyBoundaryCondition. -
Method
CreateFixedConstraintofvtkn88FiniteElementModelis renamed toFixNodes. -
Method
CreateForceConstraintofvtkn88FiniteElementModelis renamed toApplyLoad. -
Method
DataSetFromSelectionofvtkn88FiniteElementModelis deprecated.
Use either DataSetFromNodeSet or DataSetFromElementSet.
-
Method
PolyDataFromSelectionofvtkn88FiniteElementModelis deprecated.
You can duplicate this functionality as follows. Instead of
visible_bone_vertices = model.PolyDataFromSelection("bone_top")
the following code can be used instead:
reduceToPolyData = vtk.vtkGeometryFilter()
reduceToPolyData.SetInput(model.DataSetFromNodeSet("bone_top"))
reduceToPolyData.MergingOff()
reduceToPolyData.Update()
visible_bone_vertices = reduceToPolyData.GetOutput()
Note that this functionality is rarely required, as its main use was to
write node sets as VTK PolyData files (which are slightly more efficient
than VTK Unstructured Grid files). We now recommend not performing this
within scripts at all, but instead to use n88extractsets
to extract the node sets from .n88model files.
-
The names of node sets (and element sets) must be set on the data array of Point IDs.
Instead of this
model.AddNodeSet(visibleNodesIds, "bone_top")
we now write this
visibleNodesIds.SetName("bone_top")
model.AddNodeSet(visibleNodesIds)
-
Class
vtkn88FiniteElementRunis renamed tovtkn88SolverParameters. -
Specify element sets as well as node sets for post-processing. For examples, refer to the tutorials on
vtkn88, specifically Specifying sets for post-processing and Specifying sets for post-processing. -
You should make use of the History and Log fields. See any of the tutorials on
vtkn88for examples. -
Instead of
vtkn88FAIMInputWriterusevtkn88N88ModelWriter. Don’t forget to use a file name extention “.n88model” instead of “.inp”. -
Don’t specify the iteration limit for the convergence tolerance. If you really want to change these from their defaults, use the command line arguments to n88solver.
Appendix B: n88model File Format
The n88model format is a type of NetCDF4/HDF5 file. NetCDF4/HDF5 is a very widely used, high performance and robust file format for scientific and numerical data. Many standard data processing packages are able to read either NetCDF4 or HDF5, which makes it generally straightforward to import Faim data for custom processing.
|
|
The curious may be wondering how a file can be both NetCDF4 and HDF5. Historically, NetCDF and HDF were different formats. As they served largely similar purposes, starting with NetCDF 4, NetCDF adopted the HDF5 file format (amongst other options), while retaining its API or programming interface. Functionally, the NetCDF file format is a subset of HDF5, with a somewhat simpler API. HDF5 files must be structured in a specific way to be a NetCDF4 file; not any HDF5 file can be read through the NetCDF4 library. |
B.1. Converting a n88model file to and from a text file
Sometimes it is useful to examine or modify a data file by hand. Users of
faim 5.x may recall that it used a text format, which while subject to many
disadvantages, was easy to edit manually. n88model files cannot
be modified directly by hand, however they can be converted to a type of
text file, called CDL, that is human readable. Furthermore,
CDL text files, provided they are consistent with the n88model format
convention, can easily be converted back into an n88model file.
To convert an n88model file to text, the command ncdump can be used. For
example:
ncdump 1x1x2_uniaxial.n88model > 1x1x2_uniaxial.txt
|
|
You can create this example file with the command
n88modelgenerator 1x1x2.vti. The file 1x1x2.vti can be found in
the data directory of faim. It is a trivial 2-element geometry.
|
To convert it back again (perhaps after modifying it), follow this example
ncgen -k hdf5 -o 1x1x2_uniaxial.n88model 1x1x2_uniaxial.txt
B.2. Example n88model file in CDL text format
The easiest way to understand the structure of an n88model file is
to examine it in text format. Here is the 1x1x2_uniaxial.txt file,
generated in the previous section example. This model has been solved and
the file contains solution data. Although it is only two elements, the
text representation of the n88model file is rather lengthy!
netcdf \1x1x2_uniaxial {
dimensions:
Dimensionality = 3 ;
// global attributes:
:Conventions = "Numerics88/Finite_Element_Model-1.0" ;
:ActiveProblem = "Problem1" ;
:Log = "2012-Jul-18 08:59:45\nn88modelgenerator parameters:\n\ninput_file = /Applications/faim-6.0/data/1x1x2.vti\noutput_file = 1x1x2_uniaxial.n88model\ntest = uniaxial\ntest_axis = z\nstrain = -0.01\npin = off\ntop_surface = intersection\nbottom_surface = intersection\nmaterial_table = homogeneous\nyoungs_modulus = 6829\npoissons_ratio = 0.3\nconnectivity_filter = warn\n\n2012-Jul-18 09:19:26\nn88solver parameters:\n\nengine = mt\nthreads = 1\nrestart = 0\nlimit = 30000\nconvergence tolerance = 1e-06\nresidual tolerance = 0\nwindow = 4\n" ;
:History = "2012-Jul-18 08:59:45 Model created by n88modelgenerator version 6.0\n2012-Jul-18 09:19:26 Solved by n88solver version 6.0\n2012-Jul-18 09:19:26 Derived fields calculated by n88derivedfields version 6.0" ;
:ActiveSolution = "Solution1" ;
group: MaterialDefinitions {
group: NewMaterial1 {
// group attributes:
:Type = "LinearIsotropic" ;
:E = 6829. ;
:nu = 0.3 ;
} // group NewMaterial1
} // group MaterialDefinitions
group: Parts {
group: Part1 {
dimensions:
NumberOfNodes = 12 ;
variables:
float NodeCoordinates(NumberOfNodes, Dimensionality) ;
data:
NodeCoordinates =
0, 0, 0,
1, 0, 0,
0, 1, 0,
1, 1, 0,
0, 0, 1,
1, 0, 1,
0, 1, 1,
1, 1, 1,
0, 0, 2,
1, 0, 2,
0, 1, 2,
1, 1, 2 ;
group: Elements {
group: Hexahedrons {
dimensions:
NumberOfNodesPerElement = 8 ;
NumberOfElements = 2 ;
variables:
uint ElementNumber(NumberOfElements) ;
uint NodeNumbers(NumberOfElements, NumberOfNodesPerElement) ;
ushort MaterialID(NumberOfElements) ;
data:
ElementNumber = 1, 2 ;
NodeNumbers =
1, 2, 3, 4, 5, 6, 7, 8,
5, 6, 7, 8, 9, 10, 11, 12 ;
MaterialID = 127, 127 ;
} // group Hexahedrons
} // group Elements
group: MaterialTable {
dimensions:
Size = 1 ;
variables:
ushort ID(Size) ;
string MaterialName(Size) ;
data:
ID = 127 ;
MaterialName = "NewMaterial1" ;
} // group MaterialTable
} // group Part1
} // group Parts
group: Constraints {
group: bottom_fixed {
dimensions:
NumberOfValues = 4 ;
variables:
uint NodeNumber(NumberOfValues) ;
byte Sense(NumberOfValues) ;
float Value(NumberOfValues) ;
// group attributes:
:Part = "Part1" ;
:Type = "NodeAxisDisplacement" ;
data:
NodeNumber = 1, 2, 3, 4 ;
Sense = 3, 3, 3, 3 ;
Value = 0, 0, 0, 0 ;
} // group bottom_fixed
group: top_displacement {
dimensions:
NumberOfValues = 4 ;
variables:
uint NodeNumber(NumberOfValues) ;
byte Sense(NumberOfValues) ;
float Value(NumberOfValues) ;
// group attributes:
:Part = "Part1" ;
:Type = "NodeAxisDisplacement" ;
data:
NodeNumber = 9, 10, 11, 12 ;
Sense = 3, 3, 3, 3 ;
Value = -0.02, -0.02, -0.02, -0.02 ;
} // group top_displacement
} // group Constraints
group: Sets {
group: NodeSets {
group: face_z0 {
dimensions:
NumberOfNodes = 4 ;
variables:
uint NodeNumber(NumberOfNodes) ;
// group attributes:
:Part = "Part1" ;
data:
NodeNumber = 1, 2, 3, 4 ;
} // group face_z0
group: face_z1 {
dimensions:
NumberOfNodes = 4 ;
variables:
uint NodeNumber(NumberOfNodes) ;
// group attributes:
:Part = "Part1" ;
data:
NodeNumber = 9, 10, 11, 12 ;
} // group face_z1
group: face_x0 {
dimensions:
NumberOfNodes = 6 ;
variables:
uint NodeNumber(NumberOfNodes) ;
// group attributes:
:Part = "Part1" ;
data:
NodeNumber = 1, 3, 5, 7, 9, 11 ;
} // group face_x0
group: face_x1 {
dimensions:
NumberOfNodes = 6 ;
variables:
uint NodeNumber(NumberOfNodes) ;
// group attributes:
:Part = "Part1" ;
data:
NodeNumber = 2, 4, 6, 8, 10, 12 ;
} // group face_x1
group: face_y0 {
dimensions:
NumberOfNodes = 6 ;
variables:
uint NodeNumber(NumberOfNodes) ;
// group attributes:
:Part = "Part1" ;
data:
NodeNumber = 1, 2, 5, 6, 9, 10 ;
} // group face_y0
group: face_y1 {
dimensions:
NumberOfNodes = 6 ;
variables:
uint NodeNumber(NumberOfNodes) ;
// group attributes:
:Part = "Part1" ;
data:
NodeNumber = 3, 4, 7, 8, 11, 12 ;
} // group face_y1
} // group NodeSets
group: ElementSets {
group: face_z0 {
dimensions:
NumberOfElements = 1 ;
variables:
uint ElementNumber(NumberOfElements) ;
// group attributes:
:Part = "Part1" ;
data:
ElementNumber = 1 ;
} // group face_z0
group: face_z1 {
dimensions:
NumberOfElements = 1 ;
variables:
uint ElementNumber(NumberOfElements) ;
// group attributes:
:Part = "Part1" ;
data:
ElementNumber = 2 ;
} // group face_z1
group: face_x0 {
dimensions:
NumberOfElements = 2 ;
variables:
uint ElementNumber(NumberOfElements) ;
// group attributes:
:Part = "Part1" ;
data:
ElementNumber = 1, 2 ;
} // group face_x0
group: face_x1 {
dimensions:
NumberOfElements = 2 ;
variables:
uint ElementNumber(NumberOfElements) ;
// group attributes:
:Part = "Part1" ;
data:
ElementNumber = 1, 2 ;
} // group face_x1
group: face_y0 {
dimensions:
NumberOfElements = 2 ;
variables:
uint ElementNumber(NumberOfElements) ;
// group attributes:
:Part = "Part1" ;
data:
ElementNumber = 1, 2 ;
} // group face_y0
group: face_y1 {
dimensions:
NumberOfElements = 2 ;
variables:
uint ElementNumber(NumberOfElements) ;
// group attributes:
:Part = "Part1" ;
data:
ElementNumber = 1, 2 ;
} // group face_y1
} // group ElementSets
} // group Sets
group: Problems {
group: Problem1 {
// group attributes:
:Part = "Part1" ;
:Constraints = "bottom_fixed,top_displacement" ;
:PostProcessingNodeSets = "face_z1,face_z0" ;
:PostProcessingElementSets = "face_z1,face_z0" ;
:RotationCenter = 0.5, 0.5, 1. ;
} // group Problem1
} // group Problems
group: Solutions {
group: Solution1 {
// group attributes:
:Problem = "Problem1" ;
group: NodeValues {
dimensions:
NumberOfNodes = 12 ;
variables:
float Displacement(NumberOfNodes, Dimensionality) ;
float Residual(NumberOfNodes, Dimensionality) ;
float ReactionForce(NumberOfNodes, Dimensionality) ;
data:
Displacement =
-0.001500001, -0.001500001, 0,
0.001500001, -0.001500001, 0,
-0.001500001, 0.001500001, 0,
0.001500001, 0.001500001, 0,
-0.001500001, -0.001500001, -0.01000001,
0.001500001, -0.001500001, -0.01000001,
-0.001500001, 0.001500001, -0.01000001,
0.001500001, 0.001500001, -0.01000001,
-0.001500001, -0.001500001, -0.02,
0.001500001, -0.001500001, -0.02,
-0.001500001, 0.001500001, -0.02,
0.001500001, 0.001500001, -0.02 ;
Residual =
-1.528847e-07, -1.528847e-07, 0,
1.528847e-07, -1.528847e-07, 0,
-1.528847e-07, 1.528847e-07, 0,
1.528847e-07, 1.528847e-07, 0,
1.437116e-05, 1.437116e-05, 3.424616e-05,
-1.437116e-05, 1.437116e-05, 3.424616e-05,
1.437116e-05, -1.437116e-05, 3.424616e-05,
-1.437116e-05, -1.437116e-05, 3.424616e-05,
1.452404e-05, 1.452404e-05, 0,
-1.452404e-05, 1.452404e-05, 0,
1.452404e-05, -1.452404e-05, 0,
-1.452404e-05, -1.452404e-05, 0 ;
ReactionForce =
1.528847e-07, 1.528847e-07, 17.07251,
-1.528847e-07, 1.528847e-07, 17.07251,
1.528847e-07, -1.528847e-07, 17.07251,
-1.528847e-07, -1.528847e-07, 17.07251,
-1.437116e-05, -1.437116e-05, -3.424616e-05,
1.437116e-05, -1.437116e-05, -3.424616e-05,
-1.437116e-05, 1.437116e-05, -3.424616e-05,
1.437116e-05, 1.437116e-05, -3.424616e-05,
-1.452404e-05, -1.452404e-05, -17.07248,
1.452404e-05, -1.452404e-05, -17.07248,
-1.452404e-05, 1.452404e-05, -17.07248,
1.452404e-05, 1.452404e-05, -17.07248 ;
} // group NodeValues
group: ElementValues {
dimensions:
NumberOfElements = 2 ;
NumberOfStressStrainComponents = 6 ;
variables:
float Stress(NumberOfElements, NumberOfStressStrainComponents) ;
float VonMisesStress(NumberOfElements) ;
float Strain(NumberOfElements, NumberOfStressStrainComponents) ;
float StrainEnergyDensity(NumberOfElements) ;
data:
Stress =
-6.115387e-07, -6.115387e-07, -68.29005, 0, 0, 0,
5.809617e-05, 5.809617e-05, -68.28991, 0, 0, 0 ;
VonMisesStress = 68.29005, 68.28997 ;
Strain =
0.003000002, 0.003000002, -0.01000001, 0, 0, 0,
0.003000002, 0.003000002, -0.009999992, 0, 0, 0 ;
StrainEnergyDensity = 0.3414505, 0.3414495 ;
} // group ElementValues
} // group Solution1
} // group Solutions
}
B.3. Specification
NetCDF4 files consist of dimensions, variables and attributes, as well as groups. Groups can contain dimensions, variables and attributes, as well as other groups, thus forming a nested tree structure. Variables can also contain attributes.
Types specified below as “numeric” may be any concrete numeric type. Similarly “integral” may be any concrete integer type.
It is convenient to refer to the text format example when trying to follow the file specification.
|
|
In some cases dimensions may be named differently than specified below. (For complex reasons some of the n88 tools are unable to deduce the correct dimension names in certain rare cases.) This should be avoided where possible when writing a file. For reading files, the most reliable method is to inquire about the dimensions of the variables, rather than looking up dimensions by name. |
B.3.1. Root group
The root group exists for all NetCDF4 files. It does not need to be created.
- attribute [text] Conventions
-
Specifies that this is a
n88modelfile. Must be “Numerics88/Finite_Element_Model-1.0”. Required. - attribute [text] ActiveProblem
-
Specifies the problem that will be used as input to the solver. Must be set to a name of a subgroup of the Problems group. Required by the solver.
- attribute [text] ActiveSolution
-
Specifies the active solution set, which is typically the one that will be used for post-processing or rendering. Must be set to a name of a subgroup of the Solution group. Required by
n88postfaim, but not required by the solver.
- attribute [text] History
-
Brief history of the operations that have been performed on the file. By convention, add one line to the history for each operation performed on the file. Each line should start with a time/date stamp. Additional detail should go into the Log attribute. Required.
- attribute [text] Log
-
As much additional detail as required about operations that have been performed on the file. Each addition or section in Log may be multiple lines. It is recommended that each section start with a time/date stamp, in order to make it easy to correlate with History. Optional.
- dimension Dimensionality
-
Specifies the dimension of the problem. Currently it must be 3, although future versions of Faim might also support 2D models. Required.
B.3.2. MaterialDefinitions group
This group contains material definitions. Each material definition is implemented as a subgroup, where the name of the subgroup is the name of the material being defined. Each subgroup is required to have an attribute Type. Required.
- subgroups of MaterialDefinitions of Type “LinearIsotropic”
-
A subgroup that defines a linear isotropic material. Optional. As many may be defined as required.
- attribute [text] Type
-
“LinearIsotropic”. Required.
- dimension MaterialArrayLength
-
Specifies the number of materials, if a material array if being defined. Optional; if not present a single material is being defined.
- attribute [numeric] or variable E
-
Specifies the Young’s Modulus of the material, or, if a variable, a sequence of length MaterialArrayLength of Young’s Modulii for the materials. Required.
- attribute [numeric] or variable nu
-
Specifies the Poisson’s Ratio of the material, or, if a variable, a sequence of length MaterialArrayLength of Poisson’s Ratios for the materials. Required.
- subgroups of MaterialDefinitions of Type “LinearOrthotropic”
-
A subgroup that defines a linear orthotropic material. Optional. As many may be defined as required.
- attribute [text] Type
-
“LinearOrthotropic”. Required.
- dimension MaterialArrayLength
-
Specifies the number of materials, if a material array if being defined. Optional; if not present a single material is being defined.
- attribute [numeric, length 3] or variable E
-
Specifies the Young’s Modulii of the material as Exx, Eyy, Ezz. Alternatively, if a variable, must be of dimensions MaterialArrayLength×3. Required.
- attribute [numeric, length 3] or variable nu
-
Specifies the Poisson’s Ratio of the material as νyz, νzx, νxy. Alternatively, if a variable, must be of dimensions MaterialArrayLength×3. Required.
- attribute [numeric, length 3] or variable G
-
Specifies the Shear Modulus of the material as Gyz, Gzx, Gxy. Alternatively, if a variable, must be of dimensions MaterialArrayLength×3. Required.
- subgroups of MaterialDefinitions of Type “LinearAnisotropic”
-
A subgroup that defines a linear anisotropic material. Optional. As many may be defined as required.
- attribute [text] Type
-
“LinearAnisotropic”. Required.
- dimension MaterialArrayLength
-
Specifies the number of materials, if a material array if being defined. Optional; if not present a single material is being defined.
- attribute [numeric, length 36] or variable StressStrainMatrix
-
Specifies the 36 elements of the stress-strain matrix. Note that since the stress-strain matrix is symmetric, there are only 21 unique values, but for a single material all 36 must be given. They must be specified in the order K11, K12, K13 . . . K66, but since the matrix is symmetric, this is equivalent to K11, K21, K31 . . . K66. Alternatively, if a variable, must be of dimensions MaterialArrayLength×21. Note that in the case of a material array, the upper triangular packed form of the matrix stored for efficiency. Then for each material in the array the indices required are K11, K12, K22, K13, K23, K33 . . . K66 , which are the 21 unique values. Due to symmetry, this sequence is the same as K11, K21, K22, K31, K32, K33 . . . K66. Required.
- subgroups of MaterialDefinitions of Type “VonMisesIsotropic”
-
A subgroup that defines an isotropic von Mises elastoplastic material. Optional. As many may be defined as required.
- attribute [text] Type
-
“VonMisesIsotropic”. Required.
- dimension MaterialArrayLength
-
Specifies the number of materials, if a material array if being defined. Optional; if not present a single material is being defined.
- attribute [numeric] or variable E
-
Specifies the Young’s Modulus of the material, or, if a variable, a sequence of length MaterialArrayLength of Young’s Modulii for the materials. Required.
- attribute [numeric] or variable nu
-
Specifies the Poisson’s Ratio of the material, or, if a variable, a ssequence of length MaterialArrayLength of Poisson’s Ratios for the materials. Required.
- attribute [numeric] Y
-
Specifies the Yield Strength of the material, or, if a variable, a sequence of length MaterialArrayLength of Yield Strengths for the materials. Required.
- subgroups of MaterialDefinitions of Type “MohrCoulombIsotropic”
-
A subgroup that defines an isotropic Mohr Coulomb elastoplastic material. Optional. As many may be defined as required.
- attribute [text] Type
-
“MohrCoulombIsotropic”. Required.
- dimension MaterialArrayLength
-
Specifies the number of materials, if a material array if being defined. Optional; if not present a single material is being defined.
- attribute [numeric] or variable E
-
Specifies the Young’s Modulus of the material, or, if a variable, a sequence of length MaterialArrayLength of Young’s Modulii for the materials. Required.
- attribute [numeric] or variable nu
-
Specifies the Poisson’s Ratio of the material, or, if a variable, a sequence of length MaterialArrayLength of Poisson’s Ratios for the materials. Required.
- attribute [numeric] or variable c
-
Specifies the Mohr Coulomb c parameter (cohesion) of the material, or, if a variable, a sequence of length MaterialArrayLength of c values for the materials. Required.
- attribute [numeric] or variable phi
-
Specifies the Mohr Coulomb φ parameter (friction angle) of the material, or, if a variable, a ssequence of length MaterialArrayLength of φ values for the materials. Required.
- attribute [numeric] or variable psi
-
Specifies the Mohr Coulomb ψ parameter (dilation angle) of the material, or, if a variable, a sequence of length MaterialArrayLength of ψ values for the materials. Optional, assumed zero if not specified.
B.3.3. Parts group
This group defines parts. A part is a geometric collection of elements, along with the associated nodes and the material assignments for the elements. Each part is implemented as a subgroup, where the name of the subgroup is the name of the part being defined.
- subgroups of Part
-
The subgroup name gives the part name. At least one subgroup is required, and multiple ones may be defined.
- dimension NumberOfNodes
-
The number of nodes in the variable NodeCoordinates.
- variable NodeCoordinates (NumberOfNodes, Dimensionality) [numeric]
-
Specifies the x,y,z coordinates of the nodes. The node numbering is implicit, and 1-based. Hence the first row is node 1, the second node 2, etc…
- subgroup MaterialTable of subgroups of Part
-
Maps material names, as defined in MaterialDefinitions, to material ID numbers. Material ID numbers are then assigned to each element. Required by the solver.
- dimension Size
-
The number of entries in the material table for this part.
- variable MaterialName (Size) [text]
-
The material names, corresponding to subgroups in MaterialDefinitions. Required.
- variable ID (Size) [integral]
-
The IDs assigned to to materials. Any IDs in the range 1-32768 may be assigned, provided they are unique. Required.
- subgroup Element of subgroups of Part
-
Required. Currently must itself contain exactly the single subgroup, Hexahedrons.
- subgroup Hexahedron of subgroup Element of subgroups of Part
-
Defines the hexahedral elements of the part. Note that the current version of
n88solveronly handles regular hexahedrons, although the file format does not enforce this. Currently required, although in future versions supporting multiple element types, may become optional.- dimension NumberOfNodesPerElement [=8]
-
The number of nodes per element, which for hexahedrons is 8.
- dimension NumberOfElements
-
The number of hexahedral elements.
- variable ElementNumber (NumberOfElements) [integral]
-
Explicitly assigned element numbers. In the current version, the solver requires consecutively-numbered elements starting with element 1, but this restriction may be relaxed in future versions. Required.
- variable NodeNumbers (NumberOfElements, NumberOfNodesPerElement)
-
The node numbers of the nodes defining each hexahedron. The topology is as the VTK type
VTK_VOXEL, and is shown in Figure 50. The global node numbers (1-indexed) must be given for each element in the order as shown in the figure. Required. - variable MaterialID (NumberOfElements) [integral]
-
The material IDs of the materials assigned to each element. IDs correspond to values in the MaterialTable for this part. Required.
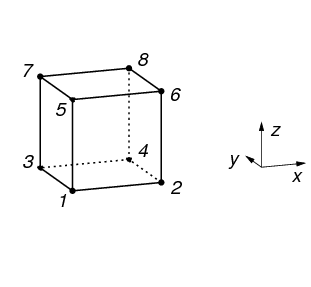
|
|
The ordering of the elements in the input file has a strong influence on the solver. Certain orderings are optimal and will solve in the fastest time. There exist orderings which will cause the solver to fail with an error. A future version of Faim might reorder the input elements as required, but in the current version, we strongly recommend that elements be ordered in the file according to “x fastest, z slowest”. |
B.3.4. Constraints group
Constraints are sets of values assigned to nodes, and used to define both boundary conditions and applied loads. Each constraint (which itself is a set of values) is implemented as a subgroup, where the name of the subgroup is the name of the constraint being defined. Optional, although a well-defined problem will always have some constraints.
|
|
vtkbone supports constraints defined on elements as well, which the
n88model file format does not currently support. This is the
natural way to define applied loads. The file writers in
vtkbone distribute element forces appropriately on to the nodes on writing.
Because of this, vtkboneN88ModelWriter and vtkboneN88ModelReader are not quite
inverses. Using them in sequence can result in a model with a different,
although physically equivalent, set of constraints.
|
- subgroups of Constraints
-
The subgroup name gives the Constraint name. Optional. Any number of subgroups may be defined.
- attribute [text] Part
-
The part to which the constraint is associated. Note that this does not necessarily imply that the constraint will in fact be applied to the named part. Refer to the attribute Constraints in the Problems group.
- attribute [text] Type
-
Currently two types are supported, NodeAxisDisplacement and NodeAxisForce. For the former, specific displacements for given nodes along given axis directions (the “sense”) are defined. The latter is similar but the specified values are forces.
- dimension NumberOfValues
-
The number of values specified by this constraint.
- variable NodeNumber (NumberOfValues) [integral]
-
A list of the node numbers to which the constraint is applied.
- variable Sense (NumberOfValues) [integral]
-
A list of the senses along which the constraint is applied. Valid values are 1,2,3 for x,y,z respectively.
- variable Value (NumberOfValues) [integral]
-
A list of the values (displacement or force) of the constraint.
B.3.5. Sets group
Sets are collections of nodes or of elements. The primary use of sets
in n88model files is for post-processing. n88postfaim requires
at least two-post processing sets of nodes, which must be matched by
sets of the corresponding elements. Quantities (e.g. the difference
between the sum of the forces on the node sets) are then calculated between
pairs of sets. A secondary use of sets is simply to store sets
that can be further refined and transformed into boundary conditions
during model generation. This is particularly useful when the model
generation occurs in several stages.
- subgroup NodeSets of Sets
-
Defines node sets. Each node set is implemented as a subgroup, where the name of the subgroup is the name of the node set being defined. Required by
n88postfaim. - subgroups of subgroup NodeSets of Sets
-
The subgroup name gives the node set name. Optional. As many may be defined as required.
- attribute [text] Part
-
The part with which the node set is associated.
- dimension NumberOfNodes
-
The number of nodes in the node set.
- variable NodeNumber
-
A list of the node numbers of the nodes in the set.
- subgroup ElementSets of Sets
-
Defines element sets. Each element set is implemented as a subgroup, where the name of the subgroup is the name of the element set being defined. Optional, although element sets must be defined if
n88postfaimis to be used. - subgroups of subgroup ElementSets of Sets
-
The subgroup name gives the element set name. Optional. As many may be defined as required.
- attribute [text] Part
-
The part with which the element set is associated.
- dimension NumberOfElements
-
The number of elements in the element set.
- variable ElementNumber
-
A list of the element numbers of the elements in the set.
B.3.6. Problems group
The Problems group defines problems that can be solved by the solver. Multiple problems may be defined. Each problem is implemented as a subgroup, where the name of the subgroup is the name of the problem being defined. In the current version, only the problem specified by the root-level attribute ActiveProblem will be solved when the file is submitted to the solver. Required by the solver.
- subgroups of Problem
-
The subgroup name gives the problem name. Optional. As many may be defined as required.
- attribute [text] Part
-
Gives the part that will be used for this problem. Required.
- attribute [text] Constraints
-
Gives a list of constraints that will be applied to the problem. Takes the form of a list of constraint names separated by commas. It is clearly a logical error to assign constraints that are associated with a different part. Required.
- attribute [numeric] ConvergenceTolerance
-
Specifies the convergence tolerance to be used by the solver. Optional, and recommended that you not set this in the
n88modelfile, because the optimum value depends on the solver. The solver will typically choose an appropriate value, but the choice can be specified with a command line option ton88solver, which is the recommended way to set the convergence tolerance should you wish to change it. - attribute [numeric] ConvergenceWindow
-
Specifies the convergence window to be used by the solver. Optional, and recommended that you not set this in the
n88modelfile, because the optimum value depends on the solver. The solver will typically choose an appropriate value, but the choice can be specified with a command line option ton88solver, which is the recommended way to set the convergence window should you wish to change it. - attribute [integral] MaximumIterations
-
Specifies the maximum iterations to be used by the solver. Optional, and recommended that you not set this in the
n88modelfile, because the optimum value depends on the solver. The solver will typically choose an appropriate value, but the choice can be specified with a command line option ton88solver, which is the recommended way to set the maximum iterations should you wish to change it. - attribute [text] PostProcessingNodeSets
-
Gives a list of node sets that will be used for post-processing. Takes the form of a list of node set names separated by commas.
n88postfaimrequires that at least two post-processing node sets to be defined.n88postfaimhas an equivalent command-line option which takes precedence.
- attribute [text] PostProcessingElementSets
-
Gives a list of element sets that will be used for post-processing. Takes the form of a list of element set names separated by commas.
n88postfaimrequires that every node set specified in PostProcessingNodeSets be exactly matched with an element set of the associated elements.n88postfaimhas an equivalent command-line option which takes precedence. - attribute [numeric, length 3] RotationCenter
-
Gives the rotation center. This value is used only for post-processing. Optional.
B.3.7. Solutions group
The solutions group contains solution values as calculated by n88solver
or n88derivedfields. Any number of solution sets may be defined
(including multiple solution sets per problem). Each solution set is
implemented as a subgroup, where the name of the subgroup is the name
of the problem being defined. The solution set specified by the root level
attribute ActiveSolution is the one that will be used for post-processing.
- subgroups of Solutions
-
The subgroup name gives the solution set name. Optional. As many may be defined as required.
- attribute [text] Problem
-
The problem to which the solution applies. Required.
- subgroup NodeValues of subgroups of Solutions
-
A group containing variables that specify values on each node. Variables are identified by name, and may be either one-dimensional (scalar values on the nodes), or two-dimensional (vector values on the nodes).
- dimension NumberOfNodes
-
The number of nodes in the problem. This is redundant with the number of nodes defined in the part, and must be equal to it. (The NetCDF4 format requires that it be re-defined here.) Required.
- typical variables in NodeValues
-
-
Displacement (NumberOfNodes, Dimensionality)
-
Residual (NumberOfNodes, Dimensionality)
-
ReactionForce (NumberOfNodes, Dimensionality)
-
- subgroup ElementValues of subgroups of Solutions
-
A group containing variables that specify values on each element. Variables are identified by name, and may be either one-dimensional (scalar values on the elements), or two-dimensional (vector values on the elements).
- dimension NumberOfElements
-
The number of elements in the problem. This is redundant with the number of elements defined in the part, and must be equal to it. (The NetCDF4 format requires that it be re-defined here.) Required.
- dimension NumberOfStressStrainComponents [=6]
-
Stress and strain are defined on the elements, and have 6 components, so a dimension equal to 6 must be defined. The order must be xx,yy,zz,yz,zx,xy.
- typical variables in ElementValues
-
-
Stress (NumberOfElements, NumberOfStressStrainComponents)
-
Strain (NumberOfElements, NumberOfStressStrainComponents)
-
VonMisesStress (NumberOfElements)
-
StrainEnergyDensity (NumberOfElements)
-
B.4. Writing code to read and write n88model files
The following methods are possible for reading and writing n88model files:
-
Use the
vtkboneclasses vtkboneN88ModelReader and vtkboneN88ModelWriter , either in C++ or in python. -
Use the python class
N88ModelReaderwhich is part of n88tools. -
Directly read or write the file with the netCDF4 library in C or C++, following the above file standard. Refer to http://www.unidata.ucar.edu/software/netcdf/docs/ for documentation on using the NetCDF interface.
-
Directly read or write the file with the netCDF4 python module (http://unidata.github.io/netcdf4-python/), following the above file standard. See for example the source file
modelinfo.pywhich is part of n88tools. If you have installed n88tools using Anaconda Python, then the netCDF4 module is automatically installed as a dependency.
Appendix C: Automating the Processing of Multiple Models With Scripts
|
|
This section currently applies only to OS-X and Linux. |
Very often one has not just a single model to solve, but a whole series of data sets that needs to be modelled by FE analysis. The section will show how to use simple shell scripts to automate this task.
|
|
We highly recommend initially running the models one at a time, and visualizing the results as you go, to ensure that your models and results are reasonable and as you expect, before sending hundreds of models to be solved in a batch script. |
|
|
Shell scripts are a standard part of any Unix-based operating system, including OS-X. If you want to learn more about shell scripting than we present here, there are many good tutorials on the web. Search for “bash scripting tutorial”. |
C.1. A script to generate a mesh and solve it
The first step to is to make a script that can generate a mesh, solve it, and
clean up, all with one command. The following shell script does this. You can
find a copy of it, named mesh_solve_analyze in the
examples/batch_processing directory of the distribution. Alternatively,
you can just copy and paste the commands below into a text editor and save
it to a file named mesh_solve_analyze .
#!/bin/bash
#
# This is a simple script that takes a segmented image file name as input,
# generates a finite element model using n88modelgenerator, then solves
# it with the FAIM solver.
#
# Assuming this script is in the current directory, it can be run as follows:
#
# ./mesh_solve_analyze image_file config_file
#
# where image_file is the segmented image file to be processed, and
# config_file is an n88modelgenerator configuration file.
#
# You may want to edit this script in order to customize it.
if [ $# -ne 2 ] ; then
echo "Usage: mesh_solve_analyze image_file config_file"
exit 1
fi
INPUT_IMAGE_FILE="$1"
MODEL_GENERATOR_CONFIG_FILE="$2"
# Strip off the extension of the input file
ROOT_FILE_NAME=`echo "${INPUT_IMAGE_FILE}" | sed 's/\(.*\)\..*/\1/'`
MODEL_FILE="${ROOT_FILE_NAME}.n88model"
date
echo
echo " ==== Generating ${MODEL_FILE} ===="
echo
n88modelgenerator --config="${MODEL_GENERATOR_CONFIG_FILE}" \
"${INPUT_IMAGE_FILE}" "${MODEL_FILE}"
if [ $? -ne 0 ] ; then
echo "Mesh generation returned error."
exit 1
fi
echo
echo " ==== Solving and post-processing FE model ===="
echo
faim "${MODEL_FILE}"
if [ $? -ne 0 ] ; then
echo "faim returned error."
exit 1
fi
echo
echo " ==== Compressing data file ===="
echo
n88compress "${MODEL_FILE}"
if [ $? -ne 0 ] ; then
echo "compress returned error."
exit 1
fi
echoIf this script does exactly what you want, it can be run directly from the installation directory, like this:
/Applications/faim-6.0/examples/batch_processing/mesh_solve_analyze input_file config_file
On Linux, Faim is typically installed in /opt rather than /Applications.
where input_file is the segmented image file to be processed, and
config_file is an n88modelgenerator configuration file. See Running n88modelgenerator for information on the configuration file
format. The very simplest configuration file might contain just a single line specifying the test type:
test = uniaxial
You can use a text editor to create this file, and save it, for example,
as myconfig.conf in your working directory.
You can also copy this script to your working data directory and customize it to your preferences. In this case you would most likely run it like this:
./mesh_solve_analyze input_file config_file
As a tiny little tutorial, you may want to try to following:
-
Copy
mesh_solve_analyzeto your working directory. -
Copy
test25a.aimfrom thedatasubdirectory of your installation to your working directory. -
Create
myconfig.confas above using a text editor, and save it to your working directory. -
Run
mesh_solve_analyze:
./mesh_solve_analyze test25a.aim myconfig.conf
|
|
The script must be made "executable" before it can be run. The script in the example directory should already be executable, but if you write your own, you may need to change permissions to make it executable before the script can be run: chmod +x mesh_solve_analyze |
Some further notes about this script:
C.2. Scripting several models
Now that we have a command to do everything required for a single data set, we can write a very simple script that will call it several times for a number of different data sets.
Here is an example. Open a text editor and copy in the following lines.
Of course, you should replace mydata1.aim, etc… with real data
file names. Save it for example as runjobs.sh.
source /Applications/faim-6.0/setenv.sh ./mesh_solve_analyze mydata1.aim myconfig.conf ./mesh_solve_analyze mydata2.aim myconfig.conf ./mesh_solve_analyze mydata3.aim myconfig.conf
It can now be run with this command:
bash runjobs.sh
|
|
Alternatively, you can make it executable with chmod +x runjobs.sh and then run it like this: ./runjobs.sh |
C.3. Unattended execution of scripts
One issue when running scripts or very long jobs is that if the Terminal in which they were started is closed, or the user logs out, the execution will stop. This is obviously undesirable. The solution is to prepend “nohup” to the command. For example:
nohup bash runjobs.sh
Now it will keep running until completed or manually stopped.
|
|
The etymology of nohup is that is is derived from "No Hang Up", which may help to remember it. |
However, if you try this, you will note that the messages that usually appear
in the Terminal to keep you informed of progress no longer appear. Where did that go? Well, the command has been
"detached" from the Terminal window so it can outlive the Terminal. nohup
instead will send all the output messages ("STDOUT" in Unix jargon) to a file named nohup.out . You can choose
to send it to a file of your choice like this:
nohup bash runjobs.sh &> runjobs.out
As well, since nothing is being output to the Terminal, you might as well get the prompt back so you can continue to use the Terminal for other purposes. Just add an ampersand to the end of the command line, like this:
nohup bash runjobs.sh &> runjobs.out &
Now you can examine runjobs.out as you like, for example with the command:
cat runjobs.out
However, it may be inconvenient to keep re-running this command if you want to monitor the progress in real time. There is a command for that too though:
tail -f runjobs.out
Here the -f flag means “follow”. The will continue to echo new lines
as they are added to runjobs.out . When you tire of watching this,
just hit CONTROL-C. This only stops the tail command; runjobs.sh
continues to execute.
Finally, when you start a process with nohup, you may need to know how to stop
it as well. If the original Terminal is still open, this is not too
difficult. First find the job number with the jobs command:
$ jobs [1]+ Running nohup ./runjobs.sh >&runjobs.out &
(Note that the $ is the command prompt - shown here to distinguish the input
from the output. Don’t type the $ character.)
In this example, the job number is 1. It can be stopped with the command
kill %1
If the original Terminal is no longer open, then it gets a little more complicated, because we will need to find the Process ID (which is system wide) instead of the Job ID (which is specific to the Terminal). This command will do it in most cases:
$ ps -A | grep runjobs.sh 55713 ttys007 0:00.00 sh ./runjobs.sh 55719 ttys007 0:00.00 grep runjobs.sh
The Process ID in this example is 55713. We can kill that process with
kill 55713
Bibliography
-
Cusano NE, Nishiyama KK, Zhang C, Rubin MR, Boutroy S, McMahon DJ, Guo XE, Bilezikian JP (2015). Noninvasive Assessment of Skeletal Microstructure and Estimated Bone Strength in Hypoparathyroidism. J Bone Miner Res. 10.1002/jbmr.2609
-
Boyd SK, Müller R, Zernicke RF (2002). Mechanical and architectural bone adaptation in early stage experimental osteoarthritis. J Bone Miner Res 17(4):687-694.
-
Boyd SK, Ammann P (2011). Increased bone strength is associated with improved bone microarchitecture in intact female rats treated with strontium ranelate: A finite element analysis study. Bone 48(5):1109-16.
-
Campbell GM, Ominsky MS, Boyd SK (2010). Bone quality is partially recovered after the discontinuation of RANKL administration in rats by increased bone mass on existing trabeculae: an in vivo micro-CT study. Osteoporos Int 10.1007/s00198-010-1283-5.
-
Gilchrist S, Nishiyama KK, de Bakker P, Guy P, Boyd SK, Oxland T, Cripton PA (2014). Proximal femur elastic behaviour is the same in impact and constant displacement rate fall simulation. J Biomech 47, 3744-3749. 10.1016/j.jbiomech.2014.06.040
-
Homminga J, Huiskes R, Van Rietbergen B, Rüegsegger P, Weinans H (2001). Introduction and evaluation of a gray-value voxel conversion technique. J Biomech 34(4):513-7.
-
Iyer SP, Nikkel LE, Nishiyama KK, Dworakowski E, Cremers S, Zhang C, McMahon DJ, Boutroy S, Liu XS, Ratner LE, Cohen DJ, Guo XE, Shane E, Nickolas TL (2014). Kidney transplantation with early corticosteroid withdrawal: paradoxical effects at the central and peripheral skeleton. J Am Soc Nephrol 25, 1331-1341. 10.1681/ASN.2013080851
-
Kim S, Macdonald HM, Nettlefold L, McKay HA (2013). A comparison of bone quality at the distal radius between Asian and white adolescents and young adults: an HR-pQCT study. J Bone Miner Res 28, 2035-2042. 10.1002/jbmr.1939
-
Maatta M, Macdonald HM, Mulpuri K, McKay HA (2015). Deficits in distal radius bone strength, density and microstructure are associated with forearm fractures in girls: an HR-pQCT study. Osteoporos Int 26, 1163-1174. 10.1007/s00198-014-2994-9
-
Macdonald HM, Nishiyama KK, Hanley DA, Boyd SK (2011a). Changes in trabecular and cortical bone microarchitecture at peripheral sites associated with 18 months of teriparatide therapy in postmenopausal women with osteoporosis. Osteoporos Int 22, 357-362. 10.1007/s00198-010-1226-1
-
Macdonald HM, Nishiyama KK, Kang J, Hanley DA, Boyd SK (2011). Age-related patterns of trabecular and cortical bone loss differ between sexes and skeletal sites: A population-based HR-pQCT study. J Bone Miner Res 26(1):50-62.
-
MacNeil JA, Boyd SK (2008). Bone strength at the distal radius can be estimated from high-resolution peripheral quantitative computed tomography and the finite element method. Bone 42(6):1203-1213.
-
Nickolas TL, Stein EM, Dworakowski E, Nishiyama KK, Komandah-Kosseh M, Zhang CA, McMahon DJ, Liu XS, Boutroy S, Cremers S, Shane E (2013). Rapid cortical bone loss in patients with chronic kidney disease. J Bone Miner Res 28, 1811-1820. 10.1002/jbmr.1916
-
Nishiyama KK, Cohen A, Young P, Wang J, Lappe JM, Guo XE, Dempster DW, Recker RR, Shane E (2014a). Teriparatide increases strength of the peripheral skeleton in premenopausal women with idiopathic osteoporosis: a pilot HR-pQCT study. J Clin Endocrinol Metab 99, 2418-2425. 10.1210/jc.2014-1041
-
Nishiyama KK, Ito M, Harada A, Boyd SK (2014b). Classification of women with and without hip fracture based on quantitative computed tomography and finite element analysis. Osteoporos Int 25, 619-626. 10.1007/s00198-013-2459-6
-
Nishiyama KK, Macdonald HM, Buie HR, Hanley DA, Boyd SK (2010). Postmenopausal women with osteopenia have higher cortical porosity and thinner cortices at the distal radius and tibia than women with normal aBMD: an in vivo HR-pQCT study. J Bone Miner Res 25 (4):882-890.
-
Nishiyama KK, Macdonald HM, Hanley DA, Boyd SK (2013). Women with previous fragility fractures can be classified based on bone microarchitecture and finite element analysis measured with HR-pQCT. Osteoporos Int 24, 1733-1740. 10.1007/s00198-012-2160-1
-
Nishiyama KK, Macdonald HM, Moore SA, Fung T, Boyd SK, McKay HA (2012). Cortical porosity is higher in boys compared with girls at the distal radius and distal tibia during pubertal growth: an HR-pQCT study. J Bone Miner Res 27, 273-282. 10.1002/jbmr.552
-
Odgaard A (1997a). Three-dimensional methods for quantification of cancellous bone architecture. Bone 20(4):315-328.
-
Odgaard A, Kabel J, Van Rietbergen B, Dalstra M, Huiskes R (1997b). Fabric and elastic principal directions of cancellous bone are closely related. J Biomech 30(5):487-495.
-
Pistoia W, Van Rietbergen B, Eckstein F, Lill C, Lochmuller EM, Rüegsegger P (2001). Prediction of distal radius failure with microFE models based on 3d- PQCT scans. Adv Exp Med Biol 496:143-51.
-
Pistoia W, van Rietbergen B, Laib A, Rüegsegger P (2001). High-resolution three-dimensional-pQCT images can be an adequate basis for in-vivo microFE analysis of bone. J Biomech Eng 123(2):176-83.
-
Stadelmann VA, Guenther C, Eberli U, Camenisch K, Zeiter S (2015a). The effects of age on implant integration. Osteologie 2, A53.
-
Stadelmann VA, Potapova I, Camenisch K, Nehrbass D, Richards RG, Moriarty TF (2015b). In Vivo MicroCT Monitoring of Osteomyelitis in a Rat Model. Biomed Res Int 2015, 587857. 10.1155/2015/587857
-
Stadelmann VA, Conway CM, Boyd SK (2012). In vivo monitoring of bone – implant bond strength by microCT and finite element modelling. Computer Methods in Biomechanics and Biomedical Engineering, DOI:10.1080/10255842.2011.648625
-
Su R, Campbell GM, Boyd SK (2006). Establishment of an architecture-specific experimental validation approach for finite element modeling of bone by rapid prototyping and high resolution computed tomography. Med Eng Phys 29(4):480-490.
-
Sutter S, Nishiyama KK, Kepley A, Zhou B, Wang J, McMahon DJ, Guo XE, Stein EM (2014). Abnormalities in cortical bone, trabecular plates, and stiffness in postmenopausal women treated with glucocorticoids. J Clin Endocrinol Metab 99, 4231-4240. 10.1210/jc.2014-2177
-
van Rietbergen B, Odgaard A, Kabel J, Huiskes R. Direct mechanics assessment of elastic symmetries and properties of trabecular bone architecture. J Biomechanics 29(12):1653-7.
-
Zderic I, Windolf M, Gueorguiev B, Stadelmann VA (2014). Monitoring of cement distribution in vertebral bodies during vertebroplasty. Bone Joint J 96-B:(SUPP 11), 183.
Index
Colophon
This documentation was written with asciidoc (http://www.methods.co.nz/asciidoc/). The PDF is generated by compiling asciidoc into DocBook (http://www.oasis-open.org/docbook/) and processing with dblatex (http://dblatex.sourceforge.net/).